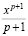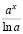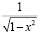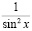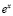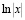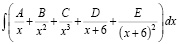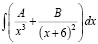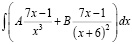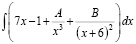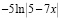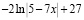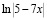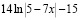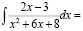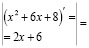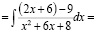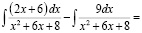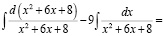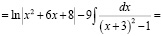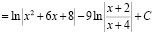Введение
В работе рассмотрены особенности математической подготовки студентов специальности «Медицинская кибернетика». Дисциплина «Высшая математика» относится к обязательной части блока С1 учебного плана и направлена на формирование универсальных и общепрофессиональных компетенций в соответствии с ФГОС ВО. Изучение высшей математики длится в течение 1–2-го семестров и включает в себя освоение следующих разделов: линейная алгебра, дифференциальное исчисление, интегральное исчисление функции многих переменных, дифференциальные уравнения, ряды.
Необходимо отметить важность рассматриваемой дисциплины для дальнейшей профессиональной подготовки студентов по специальности «Медицинская кибернетика». Так, знания, полученные в результате освоения курса высшей математики, используются в дальнейшем при изучении следующих дисциплин: «Современные информационные технологии», «Информатика», «Медицинская информатика», «Общая физика», «Квантовая физика», «Физические основы медицинских измерений», «Математическая статистика», «Вероятностные методы анализа и планирования медицинского эксперимента» и др.
Кроме того, изучение высшей математики предполагает не только освоение теоретических основ и алгоритмов решений типовых задач, но и умение применять полученные знания при решении конкретных практических задач в профессиональной деятельности, овладение навыками самостоятельного поиска методов решения той или иной задачи, умение работать со специальной математической литературой.
В реальности, как показывает многолетний опыт преподавания авторов, освоение дисциплины «Высшая математика» вызывает трудности у большинства студентов. Это можно объяснить и большим объемом изучаемого материала при малом количестве отведенных учебных часов, и сложностью самой математики, ее формализованным языком, абстрактностью понятийного аппарата, и особыми методами исследования. Но особо нужно отметить трудности, связанные с организацией интенсивной самостоятельной работы студентов, возникающие при переходе от школы к вузу [1].
Таким образом, повышение эффективности математической подготовки требует использования методов и средств интенсификации учебного процесса, например жесткого отбора теоретической информации и подбора практических задач, соответствующих большому объему изучаемой дисциплины с малым количеством отведенных аудиторных часов; продуктивной организации самостоятельной работы учащихся с возможностью самопроверки и самокоррекции уровня освоения дисциплины.
Одним из решений обозначенных проблем являются разработка и внедрение в учебный процесс рабочих тетрадей по высшей математике. Преимущества использования рабочих тетрадей в процессе обучения математике очевидны: экономия учебного времени, эффективная организация самостоятельной работы студентов с возможностью самоконтроля, возможность организации дифференцированного обучения, структурированная подача информации и др. [2]. Наиболее высокая эффективность применения рабочих тетрадей в математической подготовке достигается при выполнении определенных условий при их разработке и внедрении в учебный процесс.
Цель исследования состоит в теоретическом обосновании и разработке структуры рабочей тетради студента по высшей математике как средства интенсификации и определения педагогических условий ее эффективного внедрения в учебный процесс.
Материал и методы исследования
С целью оценки эффективности внедрения рабочих тетрадей в процесс обучения математике авторы статьи провели закрытое исследование в течение двух учебных лет, в исследование входила исследовательская группа из 32 студентов специальности «Медицинская кибернетика» Медицинского института Пензенского государственного университета (ПГУ).
В процессе исследования применялись различные методы: анализ психолого-педагогической и математической литературы; наблюдение и обобщение опыта преподавания [3].
С целью конкретизации предлагается подробно рассмотреть особенности разработки и использования рабочей тетради «Интегральное исчисление» в процессе изучения дисциплины «Высшая математика» студентами специальности «Медицинская кибернетика».
Понятие интеграла вводится еще в школе, но, как правило, рассматриваются лишь простейшие табличные интегралы, формула Ньютона–Лейбница и задачи на нахождение площади криволинейной трапеции в рамках ЕГЭ. Таким образом, у большинства студентов 1-го курса наблюдается довольно поверхностный уровень сформированных в школе знаний по данному разделу.
Раздел «Интегральное исчисление», изучаемый в вузе, достаточно объемный по содержанию и включает в себя понятие первообразной и неопределенного интеграла, основные методы интегрирования различных функций, понятие определенного интеграла и его приложения к решению практических задач, понятия несобственных интегралов. Кроме того, рассматриваемый раздел считается одним из самых сложных разделов математического анализа не только из-за сложности понятийного аппарата, но и из-за тесной связи с ранее изученным материалом школьной алгебры и геометрии и вузовской дисциплины «Высшая математика». При таких особенностях обучения сокращение аудиторных часов лишь осложняет усвоение рассматриваемого раздела.
Например, в разделе «Интегральное исчисление» вводятся в рассмотрение табличные интегралы, но на практических занятиях много времени им уже не уделяется, при этом подразумевается, что студентам известен этот материал из школы, с целью рассмотрения более сложных случаев. Но в реальности многим студентам не хватает отработки именно простых интегралов вида
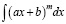 ;
; 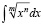 ;
; 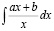
и др. Таким же образом обстоит дело с работой с определениями и теоремами; на практических занятиях невозможно тратить время на варьирование существенных признаков основных понятий и подробное рассмотрение доказательств теорем, их применения при решении задач. Очевидно, что всю эту работу студентам приходится проводить самостоятельно.
Авторами установлено, что качественная разработка и активное систематическое применение рабочих тетрадей по разделам высшей математики в учебном процессе способствуют разрешению вышеописанных трудностей и облегчению самостоятельной работы учащихся, а следовательно, и повышению качества математического образования.
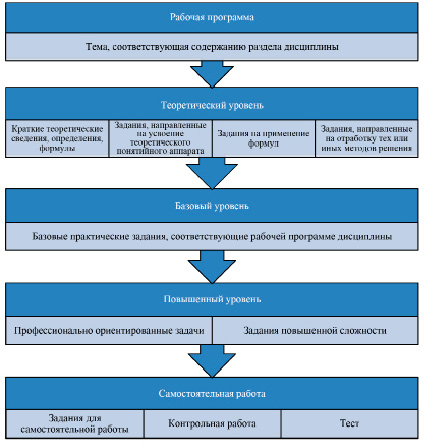
Рис. 1. Структура учебной темы
По содержанию рабочая тетрадь «Интегральное исчисление» включает в себя следующие темы в соответствии с образовательной программой дисциплины «Высшая математика» для специальности «Медицинская кибернетика»:
• Первообразная. Неопределенный интеграл и его свойства.
• Таблица основных формул интегрирования.
• Интегрирование по частям и подстановкой.
• Разложение правильной рациональной дроби на простейшие. Интегрирование рациональных дробей.
• Интегрирование простейших алгебраических иррациональностей. Интегрирование дифференциального бинома.
• Интегрирование выражений, содержащих тригонометрические функции.
• Интегрирование некоторых иррацио-нальных функций с помощью тригонометрических подстановок.
• Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла и его свойства. Формула Ньютона–Лейбница. Методы вычисления определенного интеграла.
• Несобственные интегралы с бесконечными пределами и от неограниченных функций. Признаки сходимости несобственных интегралов.
• Приложения определенного интеграла к вычислению площадей плоских фигур, объемов тел, длин дуг кривых.
Структура учебной темы представлена на рисунке 1. Каждая тема соответствует рабочей программе дисциплины и состоит из теоретического, базового, повышенного уровней заданий и заданий для самостоятельной работы, контроля усвоенных знаний.
Теоретический уровень включает в себя основные теоретические сведения, формулы, алгоритмы решений, примеры решения типовых задач, а также различные задания на усвоение теоретического материала. Например, для усвоения таблицы интегралов предлагаются следующие задания:
1) Установите взаимосвязь между функциями, записанными в левом и правом столбцах, и сделайте вывод:
|
f(x) |
F(x) |
Функция xp является _________________для функции Функция |
|
|
xp |
|
||
|
ax |
|
2) Заполните таблицу, используя взаимосвязь между первообразной F(x) и производной f(x):
|
f(x) |
F(x) |
f(x) |
F(x) |
|
|
arctg x |
sin x |
|||
|
|
|
|||
|
tg x |
cos x |
|||
|
|
|
В качестве примера заданий для усвоения определения первообразной можно привести следующие:
1) Если функция F(x) является первообразной для функции f(x) на некотором промежутке (a; b), то она должна удовлетворять следующим условиям:
1. 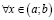 _______________ 2.
_______________ 2. 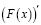 ________________
________________
2) Заполните пропуски:
Функция _____ называется первообразной для функции _____ на промежутке (a; b), если________________________________________________________________________
Базовый уровень направлен на отработку методов решения типовых задач. Например:
Вычислить следующие интегралы:
1) 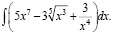 2)
2) 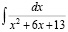 . 3)
. 3) 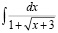 .
.
Повышенный уровень представлен нестандартными задачами, задачами повышенного уровня, профессионально ориентированными задачами [4]. Например, подобные медицинские задачи решаются с помощью интегрирования данной функции:
1) После приема таблетки содержащийся в ней лекарственный препарат начинает поступать в кровь пациента. Скорость роста концентрации препарата в крови через t минут после приема таблетки равна 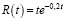 . Вычислите общее количество препарата, которое попадет в кровь в течение 10 минут после приема таблетки.
. Вычислите общее количество препарата, которое попадет в кровь в течение 10 минут после приема таблетки.
2) Найти работу при растяжении мышцы на 4 см, если для ее растяжения на 1 см требуется нагрузка 10 Н. Считать, что сила, необходимая для растяжения мышц, пропорциональна ее удлинению [5].
Также для каждой темы разработаны задания для самостоятельной, домашней работы и задания для самоконтроля и проверки усвоенных знаний, умений и навыков по рассматриваемой теме.
Пример фрагмента теста:
1. Интеграл 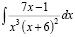 следует искать в виде:
следует искать в виде:
|
1) |
3) |
|
2) |
4) |
2. Первообразной функции 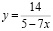 является функция
является функция
|
1) |
2) |
|
3) |
4) |
3. Формула 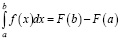 называется формулой:
называется формулой:
1) Лейбница; 2) Коши; 3) Ньютона–Лейбница; 4) Ньютона.
Разбиение задач на описанные уровни позволяет строго структурировать учебный материал, последовательно вводить его от простого к сложному, дифференцировать процесс обучения. Таким образом, рабочую тетрадь можно рассматривать как эффективное средство построения индивидуальных образовательных траекторий учащихся [3].
Как было описано выше, рабочая тетрадь по математике должна способствовать повышению эффективности и продуктивности самостоятельной работы студентов, что необходимо учитывать при организации структуры рабочей тетради.
Основываясь на исследованиях П.И. Пидкасистого, можно выделить четыре основных уровня самостоятельной работы учащихся: воспроизводящий; реконструктивно-вариативный; эвристический; творческий (исследовательский) [6].
Работа первого уровня выполняется по образцу, инструкции. При выполнении реконструктивно-вариативных самостоятельных заданий действия студентов направлены на преобразование структуры текстов и опыта решения задач. Эвристический уровень предполагает умение анализировать проблемную ситуацию, обобщать, отделять существенное от второстепенного. Самый высокий уровень самостоятельности студентов проявляется в ходе выполнения творческих самостоятельных работ.
В связи с вышесказанным разноуровневые задания в рабочей тетради вводятся последовательно от простого к сложному, от воспроизводящего до творческого уровня (табл. 1), что способствует равномерному систематическому формированию знаний, умений и навыков по изучаемой теме [7, 8].
Таблица 1
Соответствие заданий в рабочей тетради уровням самостоятельной работы студентов
|
Уровень самостоятельной работы |
Вид заданий в рабочей тетради |
Вид самостоятельной работы студентов |
Цель самостоятельной работы |
|
Воспроизводящий |
Дописать определение, формулу; кратко ответить на вопрос; решить по образцу |
Самостоятельная работа с учебником, лекционными материалами |
Закрепление знаний, формирование умений, навыков |
|
Реконструктивно-вариативный |
Восстановить цепочку решения (рассуждений), найти ошибки врешении и иное, решить задание, отличное от образца, требующее использования ранее изученного материала (дополнительных преобразований) |
Воспроизведение не только отдельных функциональных характеристик знаний, но и структуры знаний в целом. Обучение преобразовывать способ решения задачи в конкретный метод решения задач с данными условиями |
Формирование умений восстанавливать, преобразовывать, обобщать ранее полученные знания, умений и навыков устанавливать внутрипредметные связи |
|
Эвристический |
Решить задания повышенной сложности, задания, требующие поиска специальных методов решения |
Разрешение поставленной проблемной ситуации, приобретение опыта поисковой деятельности и элементов творческой деятельности |
Формирование умений и навыков поисковой деятельности |
|
Творческий |
Решить задачи на доказательство, выполнить профессионально ориентированные и практические задания |
Приобретение опыта творческой и исследовательской деятельности |
Формирование умений и навыков поисковой, творческой, исследовательской деятельности |
Примеры разноуровневых заданий
Задание воспроизводящего уровня:
Заполните пропуски:
Неопределенным интегралом функции f(x) называется ___________________, определенных на рассматриваемом промежутке.
Для второго уровня можно предложить такое задание, как:
Проанализируйте ход вычисления интеграла 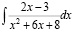 и заполните пропуски.
и заполните пропуски.
Укажите в них выполненные действия (методы) и свойства, на основе которых осуществлена замена одного интеграла другими:
|
1).
2). = 3). = 4). 5). |
1). → 2).________________________ 2). → 3).________________________ 3). → 4).________________________ 4). → 5)._________________________ |
Задание эвристического уровня требует создания проблемной ситуации, например:
Вычисляя интеграл 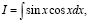 два студента получили такие результаты,
два студента получили такие результаты,
используя разные подстановки: 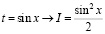 ;
; 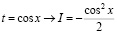 .
.
Так как оба студента считали свои вычисления верными, то они решили, что:
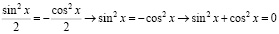 .
.
В чем ошибка студентов? Вычислите этот интеграл.
В качестве творческого задания можно рассмотреть следующее:
Пусть f(x) – монотонная непрерывная функция и f –1(x) – ее обратная функция.
Доказать, что если 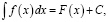 то
то 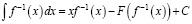 .
.
Рассмотреть примеры: а) 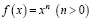 ; б)
; б) 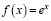 ; в)
; в) 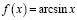 .
.
Результаты исследования и их обсуждение
На базе Медицинского института Пензенского государственного университета был организован педагогический эксперимент, целью которого являлась проверка эффективности организации математической подготовки студентов с использованием рабочих тетрадей.
Гипотеза исследования: организация математической подготовки студентов специальности «Медицинская кибернетика» с использованием рабочих тетрадей будет эффективна, если:
− определены факторы, обуславливающие структуру рабочей тетради по математике;
− выявлены, охарактеризованы и экспериментально апробированы педагогические условия эффективного использования рабочих тетрадей по математике;
− разработаны методические рекомендации по разработке рабочих тетрадей по математике.
В качестве основных показателей эффективности предложенных педагогических решений рассматривались: качество усвоения учебного материала; сформированность профессионально значимых умений; сформированность мотивации изучения математики.
Для проверки качества усвоения материала проводилось диагностирование знаний по трем уровням усвоения (теоретический, базовый, повышенный) с помощью соответствующих им заданий в форме тестирования, стандартных контрольных работ, устного опроса. Уровень сформированности профессионально значимых умений оценивали с помощью подобранных в соответствии со специальностью профессионально ориентированных заданий. Уровень мотивации изучения математики определяли посредством оценки уровня обученности в целом и умения студентов самостоятельно работать с теоретическим и практическим материалом. Описанные показатели оценивали в комплексе, определяли уровень обученности математике (низкий – 0–60 баллов, средний – 61–86 баллов, высокий – 87–100 баллов). Используемые диагностические материалы предварительно были проверены на надежность и валидность.
Курс высшей математики в контрольной группе преподавался традиционным способом в рамках лекционно-семинарской системы обучения. В экспериментальной группе обучение проходило с активным использованием рабочих тетрадей по математике. На рисунке 2 представлены обобщенные результаты измерения комплекса выделенных показателей у студентов специальности «Медицинская кибернетика» экспериментальной и контрольной групп на заключительном этапе эксперимента. В ходе эксперимента количество студентов среднего и высокого уровней экспериментальной группы стало существенно превышать аналогичный показатель для контрольной группы, а количество студентов низкого уровня в экспериментальной группе снизилось (рис. 2).
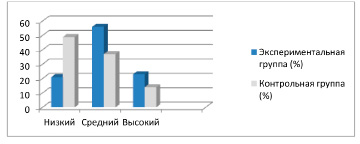
Рис. 2. Гистограмма контрольной и экспериментальной групп после окончания эксперимента
Таким образом, сопоставление результатов выполнения диагностических работ студентами контрольной и экспериментальной групп показало наиболее высокую эффективность математической подготовки с активным использованием рабочих тетрадей.
Выводы
В ходе эксперимента авторами выявлен ряд педагогических условий эффективного использования рабочих тетрадей по математике при обучении студентов медицинских направлений.
1. Обеспечение предварительной подготовки студентов по теоретическим вопросам рассматриваемой темы. Для этого в рабочей тетради перед каждым практическим блоком указываются необходимые для изучения теоретические сведения, приводятся основные формулы, определения, теоремы, правила.
2. Последовательное выполнение студентами всех предложенных заданий, чему способствуют разработанная структура каждой учебной темы, разбиение предложенных практических заданий по степени сложности и по уровням самостоятельной работы.
3. Преемственность аудиторной и самостоятельной работы студентов. Обязательное выполнение всех домашних заданий способствует непрерывному, последовательному формированию знаний, умений и навыков.
4. Обязательное выполнение заданий для самоконтроля с последующим анализом допущенных ошибок, выполнением работы над ошибками, восполнением пробелов в изученном материале.
В качестве методических рекомендаций по разработке рабочей тетради по математике авторы выделили следующие.
1. Теоретический учебный материал должен способствовать закреплению, расширению и углублению сформированных знаний, умений и навыков.
2. Практические задания должны быть ориентированы на систематизацию и обобщение полученных знаний и умений, анализ и оценку достижений.
3. Задания подбираются таким образом, чтобы развивать у студентов готовность и умение самостоятельно выбирать и применять освоенные методы.
4. Задания должны быть разноплановыми и разноуровневыми и включать профессионально ориентированные задачи.
Таким образом, рабочая тетрадь по математике как дидактическое средство способствует не только интенсификации образовательного процесса, но и последовательному, непрерывному изучению материала, поэтапному формированию знаний, умений и навыков, эффективной организации самостоятельной работы студентов, играет важную роль в реализации принципов дифференциации и профессиональной направленности обучения. Выполнение указанных педагогических условий использования рабочей тетради в учебном процессе обеспечивает качественную математическую подготовку.




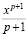
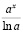 является _________________для функции ax.
является _________________для функции ax.