Введение
При формировании, описании и интеллектуальном анализе данных, представляющих собой комплексный проблемно-ориентированный библиотечно-музейно-архивно-информационный массив (БМАИМ) по нобелистике, функционирующий в реальном масштабе времени [1], сотрудники постоянно сталкиваются с условиями неопределенности, которые возникают из-за неоднозначности отнесения каждого элемента нобелистики к этому массиву. Вносить или не вносить ту или иную книгу, музейный, архивный или электронный документ в БМАИМ – такая альтернатива сопровождает каждого сотрудника, так как практически каждый документ включает в себя множество тематических рубрик, смыслов, субъективных суждений, ассоциаций. Из всех классов неопределенностей в данной ситуации главенствует сущностная, которая лежит в сути изучаемых объектов или явлений (процессов).
Известно множество методов моделирования процесса принятия решений в условиях неопределенности [2–4], например аппарат теории вероятностей, теории игр, расплывчатого множества и др. По теме исследования имеются и патенты, например [5]. Однако большинство работ посвящено конкретным ситуациям, например техническим объектам [6], бизнес-процессам [7], экономике в целом [8] и др. Использование каждой конкретной модели для иной ситуации связано со значительными трудностями доработки или переработки, осложняемыми к тому же значительным субъективизмом лица, принимающего решение (ЛПР), в основном из-за растущей многокритериальности [9].
Цель исследования – смоделировать процесс принятия решений о внесении того или иного документа в БМАИМ в условиях сущностной неопределенности и при заданном для ЛПР большом количестве критериев.
Материалы и методы исследования
Базой для проведения исследования стал БМАИМ по нобелистике Международного Информационного Нобелевского Центра (МИНЦ), так как он одновременно содержит библиотечные, музейные, архивные и электронные документы проблемно-ориентированного характера. Сущностная неопределенность проявляется в том, что большое количество поступающих объектов не содержит внешних признаков, позволяющих воспользоваться набором критериев для ЛПР. Поэтому ЛПР вынужден знакомиться с содержательной стороной объекта, на что уходит много времени и усиливается субъективизм. Для моделирования использован модифицированный подход к процессу принятия решения из пяти этапов [10]: 1) формирование множества решений и множества состояний среды комплектования; 2) введение показателей эффективности и полезности, входящих в расчет оценочного функционала; 3) определение руководством МИНЦ ситуации, характеризующей стратегию поведения среды комплектования; 4) выбор критерия принятия решений из множества критериев, характеризующих ситуацию; 5) принятие по выбранному критерию оптимального решения по введению или невведению документа в БМАИМ.
Математический аппарат для моделирования выбран из предположения о семи информационных ситуациях, которые могут возникнуть в процессе принятия решений в условиях неопределенности [11, с. 142–160; 12, с. 220–232]: 1) известна совокупность вероятностей на элементах множества выбираемых документов (используем следующие критерии принятия решений – критерий Байеса, критерий максимальной вероятности, модальный критерий, критерий минимальной дисперсии, критерий минимума энтропии математического ожидания, модифицированный критерий); 2) известно распределение вероятностей с неизвестными параметрами (параметрический критерий Байеса, параметрический критерий максимума вероятности оценочного функционала (ОФ), параметрический критерий минимума дисперсии ОФ, параметрический модальный критерий, параметрический критерий максимума энтропии математического ожидания ОФ); 3) известна система линейных отношений порядка на компонентах распределения состояния среды комплектования (тип отношений порядка задается лицом, принимающим решения, на базе имеющихся у него информации и опыта, ситуации и условий принятия решений); 4) неизвестно распределение вероятностей на элементах множества комплектования (критерий максимальных мер множеств Байеса, максимум интегрального значения Байеса, наибольший интегральный потенциал, критерий Бернулли – Лапласа, критерий Хоменюка, критерий Гиббса – Джейнса); 5) имеются антагонистические интересы среды комплектования (критерий Вальда, критерий Савиджа, функция неопределенности); 6) заданы промежуточные случаи выбора средой комплектования своих состояний (критерий Гурвица, критерий Ходжеса – Лемана, критерий Менгеса, критерий Шнейвайса); 7) задано нечеткое множество состояний среды (приведение субъективного распределения вероятностей значений компонент функции принадлежности, критерий типа вероятности распределения значений ОФ, критерий типа дисперсии значений ОФ, критерий модального типа).
Результаты исследования и их обсуждение
Определим положительные и отрицательные ОФ, которые характерны для активно направленных систем. Именно такими являются системы, обеспечивающие решение задач отнесения каждого элемента нобелистики к БМАИМ. С понятием ОФ обычно связывают расчеты эффективности, полезности, потерь, риска и т.п.
Оценочный функционал F+ используем для выражения полезности, выигрыша, эффективности, вероятностей достижения цели, а оценочный функционал F¯ применим для выражения проигрыша, сожалений, риска. Понятно, что предпочтительнее положительная форма выражения ОФ, но в ряде случаев необходимо и отрицательное значение.
Функция сожалений есть линейное преобразование положительного или отрицательного значения ОФ к относительным единицам измерения. Такое преобразование устанавливает начало отсчета ОФ «нуль» для каждого состояния среды θj (j = 1, 2 … n): 1) для F+ в случае фиксированного состояния среды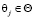 
(Θ – множество состояний среды) находится величина 
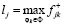(l – , Ф – множество решений из φk, f+ – текущее значение F+), и функция сожалений определяется в виде 
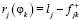; 2) для F¯ в случае фиксированного состояния среды 
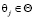находится величина 
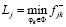и функция сожалений определяется в виде 
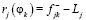. Функция сожалений имеет отрицательную форму оценочного функционала F¯, 
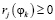, и rj = 0 хотя бы для одного решения φk при 
.
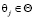Ситуации принятия решений формализуются моделью кортежа {Ф, Θ, F}, откуда можно определить различные информационные ситуации I (перечислены выше). Критерий принятия решения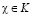 
является алгоритмом, который определяет единственное оптимальное решение 
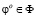либо множество решений для каждой ситуации принятия решения {Ф, Θ, F} и информационной ситуации [13, с. 28–40]. Основные критерии принятия решений в информационной ситуации I1 задаются распределением вероятностей 
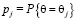.Если задана модель кортежа {Ф, Θ, F}, то задача принятия решения состоит в том, что органу принятия решения необходимо выбрать одно решение, оптимальное по выбранному критерию. Предположим, задана ситуация принятия решения {Ф, Θ, F} с заданными множествами Ф, Θ и F, с оценочными функционалами F+ или F¯. Смоделируем для этой ситуации семь основных критериев принятия решения по введению какого-либо элемента в БМАИМ [14, 15].
1. Критерий Байеса (максимизация математического ожидания оценочного функционала, преобразование априорных вероятностей в апостериорные). Оптимальными решениями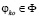 
будут такие, для которых математическое ожидание ОФ достигает максимума из возможных:
.
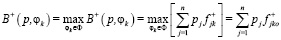Здесь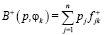 
представляет собой значение оценочного функционала Байеса для решения 
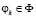. Первостепенное значение этого критерия для информационной ситуации I1 объясняется его тесной связью с аксиомами теории полезностей Наймана и Моргенштерна, в которых суммарная полезность определяется как математическое ожидание частных полезностей.
2. Критерий максимизации вероятности распределения ОФ. Введем величину α, удовлетворяющую неравенствам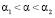 
, где 
, 
, 
, 
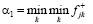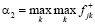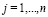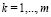. Смысл критерия в том, чтобы найти решение 
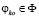, для которых соблюдается 
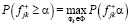. Для конкретных α и φk неравенство 
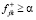определяет Θα,k. Тогда вероятность 
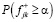равна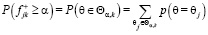 
. В этом критерии величину α задает БМАИМ, поэтому множество Ф зависит от α. Для двух значений α* и α**, таких, что 
, 
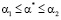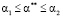и 
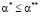имеем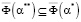 
. Кроме того, 
.
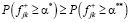3. Критерий минимума дисперсии ОФ. Смысл критерия в определении для каждого решения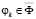 
среднего значения 
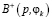ОФ (F+) и дисперсии 
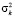в виде
.
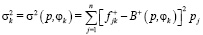На практике приходится несколько видоизменять вычисление дисперсии, например, таким образом:
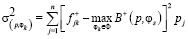или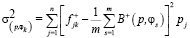 
.
Если ОФ в виде F¯, то решение φko по критерию минимума ОФ находится из условия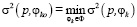 
. где величина 
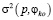определяется одним из следующих способов:
, 
,
.
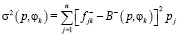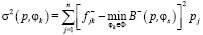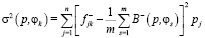4. Модальный критерий (смысл его в том, что руководство БМАИМ исходит из наиболее вероятного состояния среды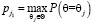 
), тогда оптимальное решение определяется из условия 
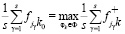. Главное достоинство критерия в выявлении самых вероятных состояний среды, для которых и производится расчет ОФ, что значительно ускоряет процесс принятия решений в условиях неопределенности.
5. Критерий минимума энтропии математического ожидания ОФ заключается в нахождении φko по условию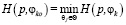 
, в котором энтропия математического ожидания ОФ определяется по формуле
.
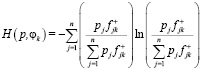Если принятое решение отрицательное, то используется другая формула:
.
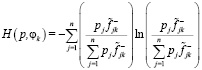6. Модифицированный критерий устанавливает λ при условии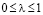 
и заключается в нахождении решения φko из условия 
.
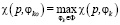При значениях λ = 0 или 1 этот критерий совпадает с первым критерием Байеса.
Для выбора λ в интервале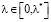 
предложим следующие точечные оценки: 
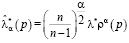. Здесь ρ(p) – расстояние от 
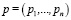до средней точки 
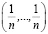плоского множества 
, равное
.
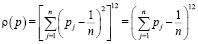Точечные оценки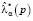 
удовлетворяют следующим двум аксиомам: 1) 
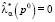при ρ(p0) = 0, то есть в случае равномерного распределения 
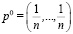модифицированный критерий совпадает с критерием Байеса; 2) 
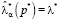при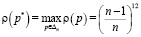 
, то есть в случае вырожденного распределения p* (одна из компонент которого равна единице, остальные – нулю) дисперсия 
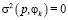для любого 
.
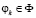Частными случаями точечных оценок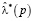 
при α = 0,1,2 являются величины
, 
, 
.
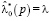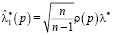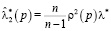Для выбора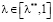 
используются точечные оценки вида
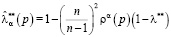с неотрицательными α.
Величины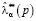 
удовлетворяют следующим двум аксиомам:
1) 
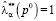при ρ(p0) = 0, то есть в случае равномерного распределения 
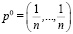модифицированный критерий совпадает с критерием минимума дисперсии;
2) 
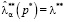при 
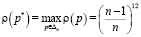, то есть в случае вырожденного распределения 
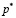дисперсия 
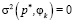для любого 
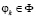и оптимальное решение принимается по критерию Байеса.
Таким образом, если руководство БМАИМ считает, что величина λ в модифицированном критерии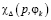 
удовлетворяет неравенствам 
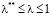, то при использовании точечной оценки 
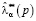принимается решение из условия максимума 
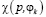по 
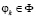для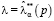 
. Частными случаями точечных оценок 
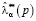при α = 0,1,2 являются
, 
, 
.
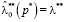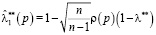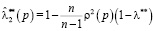Для выбора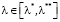 
можно предложить следующие точечные оценки:
1) 
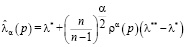, где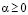 
, при этом точечные оценки удовлетворяют следующим двум аксиомам: 1) 
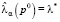при ρ(p0) = 0, то есть в случае равномерного распределения 
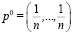в модифицированном критерии большее предпочтение дается критерию Байеса; 2)
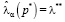при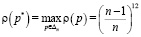 
, то есть в модифицированном критерии большее предпочтение дается критерию минимума дисперсии 
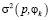, причем 
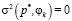для любого 
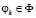и решение принимается по критерию Байеса. Частными случаями точечных оценок 
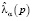при α = 0,1,2 являются
, 
, 
.
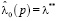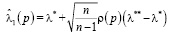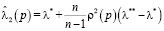7. Условные решения. Руководство БМАИМ выделяет один критерий, который называют главным, а на остальные критерии принятия решений из множества K1 налагаются ограничения; такое решение назовем условным. Для задач оптимизации и принятия решений характерным является задание ограничений либо в форме неравенств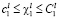 
, либо в форме равенств 
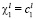. Поскольку поиск оптимального решения сводится к перебору конечного числа вариантов, то задание ограничения в форме точного равенства в большинстве случаев является не совсем корректным и приводит к отсутствию условного решения. В противоположность этому ограничения в форме неравенств являются более естественными и позволяют руководству БМАИМ проводить своеобразный анализ по установлению пределов значений величин 
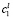и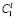 
нижней и верхней границ значений критерия 
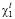. Например, включить ту или иную книгу в БМАИМ можно только при наличии упоминания в ней хотя бы одного лауреата Нобелевских премий или члена семейства Нобелей (нижний критерий).
Таким образом, если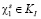 
– главный критерий, то условные решения находятся из следующей задачи:
, 
, (
; 
).
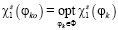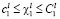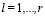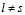Частным случаем сформулированной задачи поиска условных решений является случай, рассматривающий вместо множества KI подмножество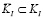 
.
Пример. Пусть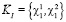 
, где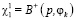 
, 
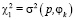, причем вектор априорного распределения 
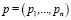задан, а 
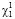– главный критерий. Ограниченное решение φko находится из условия
, 
,
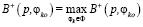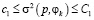где c1, C1 – заданные положительные константы. Можно определить класс условных решений и без выделения главного критерия принятия решения непосредственно как решение системы неравенств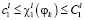 
(
).
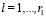Заключение
Очевидным является утверждение, что в соответствии с построенной совокупностью моделей принятие решений в каждой статической информационной ситуации приводит к необходимости разработки целенаправленных методов в зависимости от рассмотренных критериев. Такие возможности представлены и опробованы авторами в виде описанных моделей. Это не касается вопросов принятия решений в динамике, которые необходимо рассматривать на основе совершенно иных математических выкладок.