Введение
В последние годы наблюдается тенденция перехода большинства разрабатываемых нефтяных месторождений на завершающую стадию разработки. Для таких систем характерно увеличение уровня обводненности продукции порядка 60–70 % и выше [1]. При этом дебиты скважин по нефти становятся малорентабельными, а закачка неэффективной [2]. Одновременно наблюдается усложнение самих объектов добычи нефти и газа, а также технологий их разработки. Это требует совершенствования систем проектирования и управления разработкой нефтяных месторождений, позволяющих осуществлять выбор наиболее приемлемых технологий извлечения запасов углеводородов в заданных природных и экономических условиях.
При решении задач прогнозирования и проектирования разработки нефтяных месторождений одним из важнейших этапов является процесс рационального размещения эксплуатационных скважин в пласте [3]. Это можно достичь за счет оптимального управления режимами работы добывающих и нагнетательных скважин, обеспечивающими наиболее полное вовлечение в разработку низкопроницаемых зон и более полную выработку запасов в целом [2]. Такое управление включает в себя такие задачи, как: 1) найти оптимальное размещение нагнетательных скважин при заданном расположении добывающих скважин; 2) определить добывающие скважины из эксплуатационного фонда, которые целесообразно перевести в фонд нагнетательных скважин; 3) изменение или перераспределение приемистостей нагнетательных скважин [4, 5]. Вторую задачу можно обобщить и рассматривать вопрос включения в систему заводнения новых нагнетательных скважин, например путем бурения в районах высокой нефтедобычи.
Наиболее распространенный подход к управлению разработкой месторождений основан на трехмерном гидродинамическом моделировании [6–8]. Однако этот подход имеет ряд недостатков: широкий набор кондиционных результатов лабораторных исследований, скважинных и промысловых данных, огромные неопределенности моделей из-за отсутствия знаний о строении межскважинного пространства, проявление масштабных эффектов при переносе керновых данных на ячейки гидродинамической модели, необходимость многократного численного решения описывающих пластовые процессы систем дифференциальных уравнений в частных производных, обеспечивающих высокую точность решения [5, 9]. Поэтому необходимы альтернативные подходы, основанные на менее ресурсоемких математических моделях пласта. Одним из них является использование емкостно-резистивных аналитических моделей (CRM, Capacitance Resistive Model), описывающих динамический материальный баланс в виде временного ряда [1].
В статье рассматривается CRM-модель в варианте CRMP с L > 1 добывающих и M > 1 нагнетательных скважин. Для каждой добывающей скважины в k-й момент времени дебит жидкости описывается как [10]
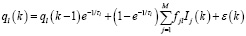 , (1)
, (1)
где τl > 0 – постоянная времени (определяет скорость распространения возмущений в пласте), fjl ≥ 0 – коэффициент взаимовлияния нагнетательной скважины Ij и добывающей скважины Pl, ε(k) – присутствующие в реальных данных случайные погрешности, k – номер периода (месяца), l = 1,…L, j = 1,…,M, k = 1,…,N.
В (1) сделано допущение о постоянстве забойного давления.
Повышение эффективности «зрелых» систем заводнения на нефтяных месторождениях требует решения задач мониторинга, прогнозирования добычи нефти, а также планирования и оптимизации объемов закачки воды. Для этого необходимо, используя данные о приемистости нагнетательных и дебите добывающих скважин, определить коэффициенты взаимовлияния и постоянные времени. На основе полученных параметров можно рассчитать оптимальное перераспределение закачиваемой воды. Наличие большого числа скважин, невыпуклый характер функциональной зависимости и наличие ряда ограничений на допустимую область значений приводит к неединственности решения и трудоемкости его нахождения [1].
В [10] предложен новый подход для CRM-моделирования, основанный на определении маски взаимовлияния. Под маской взаимовлияния понимается множество нагнетательных скважин, влияющих на формирование дебита, и соответствующие значения коэффициентов взаимовлияния fjl между нагнетательными и добывающими скважинами [10]. Данный подход позволил сократить число определяемых коэффициентов взаимовлияния, тем самым снизив размерность задачи оптимизации. В [11] предложенный подход был усовершенствован путем уменьшения объема обучающей выборки данных и расширения анализируемой системы с нескольких десятков до сотен скважин.
Цель исследования – повышение эффективности эксплуатации «зрелых» систем заводнения на основе емкостно-резистивных моделей материального баланса.
Материалы и методы исследования
Одной из сложностей при оценке параметров CRM-модели является большое количество добывающих и нагнетательных скважин, которое на практике может достигать сотен и даже тысяч. Это приводит к значительному увеличению числа возможных пар взаимовлияния, что, в свою очередь, создает вычислительную неустойчивость. На самом деле, на дебит каждой добывающей скважины Pl, l = 1,…L, влияют не все нагнетательные скважины, а лишь некоторая их часть. Определение и использование такого множества переменных поможет избежать снижения точности оценок коэффициентов взаимовлияния [10].
В [11] авторы рассматривали задачу оценивания CRM-модели в 3 этапа: 1) формирование предварительной маски взаимовлияния; 2) уточнение маски взаимовлияния и формирование начального приближения для CRM-модели; 3) определение параметров CRM-модели для всей системы заводнения. Авторами установлено, что применение маски взаимовлияния позволило снизить размерность задачи оптимизации и повысить точность CRM-моделирования. Предложенные алгоритмы определения параметров CRM-модели для всей системы заводнения продемонстрировали устойчивость к случайным ошибкам и обеспечили достаточно точные прогнозы.
Установленные в ходе оценивания CRM-модели коэффициенты взаимовлияния скважин, постоянные времени, а также исходные данные о приемистостях нагнетательных скважин и дебите добывающих скважин используются в задаче перераспределения закачиваемой воды. Оценка значений приемистости для каждого наблюдения производилась на основе оцененных параметров CRM-модели, значениях приемистостей и дебитов с помощью максимизации суммы дебитов с ограничениями на значения приемистостей:
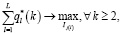 (2)
(2)
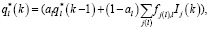 (3)
(3)
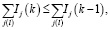 (4)
(4)
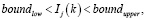
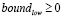 ,
, 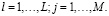 (5)
(5)
Для оценки значений приемистостей в периоде прогноза для T наблюдений последовательно вычисляются T задач (2)–(5). Также установлен предел для значения суммарного объема приемистостей в периоде прогноза. Решения оптимизационной задачи (2)–(5) могут быть получены методами:
1) метод «highs-ds» [12] – реализация симплекс-метода из библиотеки SciPy;
2) алгоритм ветвей и отсечений (COIN-OR Branch and Cut) – метод комбинаторной оптимизации для решения целочисленных линейных программ из библиотеки PULP [13];
3) решатель «GLPK» (GNU Linear Programming Kit) из библиотеки CVXOPT [14];
4) метод перемещения асимптот (MMA) из библиотеки NLOPT [15].
На модельных данных предложенные алгоритмы показывают одинаковые результаты уменьшения обводненности на ~10 %, однако метод «highs-ds» работает в 7,2 ÷ 10 раза быстрее.
Рассмотрим модельный пример системы заводнения нефтяного месторождения с тремя вариантами постепенного увеличения количества скважин определенного типа при неизменном общем объеме приемистостей. Так, в первом варианте увеличивается количество нагнетательных скважин. Во втором варианте увеличивалось количество добывающих скважин. В третьем варианте происходит одновременное увеличение количества нагнетательных и добывающих скважин.
а) 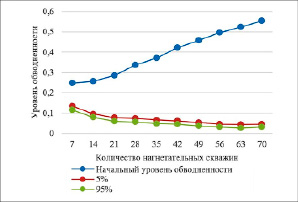
б) 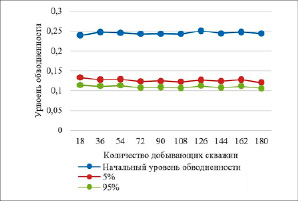
в)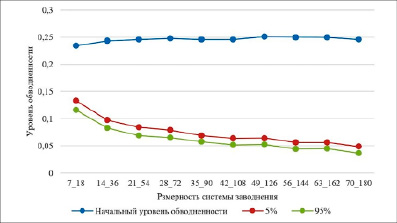
Рис. 1. а) увеличение количества нагнетательных скважин, б) увеличение количества добывающих скважин, в) одновременное увеличение размерности системы заводнения
Начальная размерность системы заводнения: 18 нагнетательных и 7 добывающих скважин. Приемистости нагнетательных скважин – это модель с системы заводнения, для каждой скважины Ij, j = 1,…,M имеется по N = 18 наблюдений, зафиксированных через равные интервалы времени. Матрица коэффициентов взаимовлияния fjl формировалась случайным образом с учетом нормировки
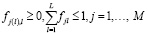 ,
,
для каждой добывающей скважины число ненулевых коэффициентов взаимовлияния выбиралось случайным образом от 1 до 6. Постоянные времени τl формировались случайным образом в диапазоне от 1 до 6. Дебиты добывающих скважин Pl формировались по формуле (1).
После оценки коэффициентов взаимовлияния, постоянных времени выполнялась оценка приемистостей за 5 наблюдений в периоде наблюдений.
На рисунке 1 представлены различные графики изменения уровня заводненности в зависимости от изменения размерности системы заводнения. Для каждой размерности смоделировано 200 наборов данных. Суммарное объем приемистостей – 15000. На графики вынесено значение начального уровня обводненности продукции ~23 %, 5-й и 95-й перцентили после оценки значений приемистостей в периоде наблюдений.
Рис. 1, а–в, демонстрируют уменьшение значения уровня обводненности продукции. Так, на рис. 1, б, показано уменьшение обводненности на ~12 %. Однако на рис. 1, а, и 1, в, наблюдается дополнительная тенденция уменьшения уровня обводненности продукции. Общим для этих случаев является увеличение количества нагнетательных скважин.
На основе полученных данных можно сделать вывод о том, что увеличение количества нагнетательных скважин позволяет уменьшить обводненность продукции.
Рассмотрим модельный пример системы, в котором к более рентабельным добывающим скважинам добавим новые нагнетательные скважины. Физически такой процесс представляет собой бурение дополнительных нагнетательных скважин в районах высокой нефтедобычи. Система состоит из 10 нагнетательных скважин и 20 добывающих скважин. Формирование исходных данных идентично формированию данных из первого примера. Так, после выполнения задачи максимизации дебитов в периоде наблюдения (2)–(5) для добывающих скважин, показавших высокие показатели нефтедобычи, добавим в маску коэффициентов взаимовлияния несколько нагнетательных скважин. После чего снова оценим параметры CRM-модели для всей системы заводнения. Затем произведем оценку значений приемистостей в периоде наблюдений при зафиксированном общем объеме приемистостей нагнетательных скважин.
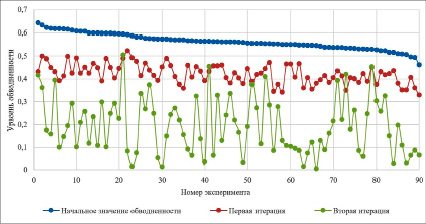
Рис. 2. Результаты вычисления уровня обводненности после добавления нагнетательных скважин в зону повышенной нефтеотдачи
Период наблюдений составил 10 наблюдений. Задано требование, чтобы суммарный объем приемистостей в периоде наблюдений не превышал установленного предела. Приемистости по скважинам подбираются в диапазоне от 0 до 250 м3/наблюдение.
Опишем алгоритм эксперимента:
1) генерация начальных данных приемистостей, дебитов, постоянных времени и коэффициентов взаимовлияния;
2) формирование предварительной маски взаимовлияния;
3) уточнение маски взаимовлияния и формирование начального приближения для CRM-модели;
4) определение параметров CRM-модели для всей системы заводнения;
5) оценивание приемистостей в периоде наблюдений с помощью максимизации суммы дебитов (2)–(5);
6) определение добывающих скважин с высоким уровнем нефтедобычи;
7) добавление в матрицу коэффициентов взаимовлияния из п. 4 коэффициентов нагнетательных скважин, не участвующих раньше в CRM-модели, инициализация предварительных значений приемистостей для новых нагнетательных скважин;
8) повторение п. 4;
9) оценивание приемистостей в периоде наблюдений с помощью максимизации суммы дебитов (2)–(5).
На рис. 2 представлены результаты таких вычислений. Под первой итерацией на рис. 2 подразумевается выполнение п. 1 – п. 5 алгоритма эксперимента, а под второй – п. 6 – п. 9. Уровень обводненности продукции ~56 %. После первой итерации значение данного показателя ~42 %. После выполнения второй итерации среднее значение обводненности составило 19 %.
Заключение
Результаты экспериментов демонстрируют эффективность использования CRM-моделирования при мониторинге «зрелых» систем заводнения. Так, на основе полученных в результате оценки CRM-модели коэффициентов взаимовлияния, постоянных времени, возможно построить не только модель для прогнозирования уровня нефтедобычи, но и модель управления системой заводнения.
Метод оценки значений приемистостей в периоде прогноза позволил снизить уровень обводненности нефти на ~12 %. А добавление в маску взаимовлияния новых нагнетательных скважин позволило уменьшить данный показатель на ~37 % при том же объеме приемистостей.
В рассмотренных алгоритмах матрица коэффициентов взаимовлияния вычислялась единожды до выполнения оценки приемистостей в периоде наблюдений. Однако после каждого наблюдения фильтрационные свойства пласта меняются, что должно своевременно учитываться в CRM-модели. Дальнейшим улучшением алгоритма является оценка матрицы коэффициентов взаимовлияния после каждого наблюдения.
Полученные алгоритмы после успешной апробации на реальных данных представляется возможным использовать для мониторинга и управления на «зрелых» системах заводнения.



