Введение
Подробный анализ современных работ, посвященных исследованию методов построения решений задач синтеза линейного регулятора, имеется в [1; 2]. Кроме того, можно отметить работы [3–5], в которых за последние десять лет в различных постановках исследованы дискретные задачи синтеза оптимального регулятора. Дискретные задачи оптимального управления рассмотрены и в наших работах [6–8]. В частности, задача конструирования регулятора для дискретной управляемой системы с малым шагом в детерминированных случаях рассмотрена в работе [6, с. 16]. Данная работа является продолжением вышеуказанных работ.
Материалы и методы исследования
Задана модель объекта управления, которая описывается уравнением
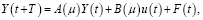 (1)
(1)
где Y(t) – вектор состояния: 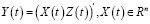 ,
, 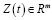 ;
;
A(μ) и B(μ) – матрицы состояния и управления:
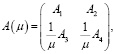
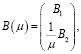
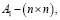
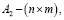
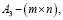
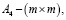
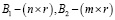 ;
;
u(t) – вектор управления; t – время переходного процесса:
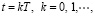 T – малый шаг, 0 ≤ T ≤ 1, μ – малый параметр,
T – малый шаг, 0 ≤ T ≤ 1, μ – малый параметр,
0 < μ < 1 штрих обозначает транспонирование, M – математическое ожидание;
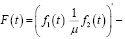 вектор внешних возмущений, последовательность взаимно независимых, гауссовских случайных векторов, некоррелированных с Y0 и удовлетворяющих условиям:
вектор внешних возмущений, последовательность взаимно независимых, гауссовских случайных векторов, некоррелированных с Y0 и удовлетворяющих условиям:
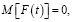
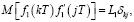
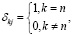
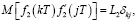
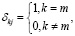
L1, L2 – симметрические, неотрицательно определенные матрицы [9, с. 41].
Начальные состояния системы (1) имеют вид
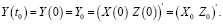 (2)
(2)
Задан критерий
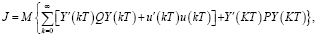 (3)
(3)
где Q, P – заданные неотрицательно определенные симметрические матрицы,
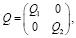
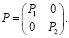
Требуется найти управление u*(t), при котором функционал (3) принимает наименьшее возможное значение, при ограничениях (1) и (2).
Предположим, что выполняется следующее условие.
Условие 1. Пусть A4 – устойчивая матрица, это означает, что собственные значения матрицы A4 удовлетворяют неравенству 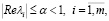 где α – некоторая постоянная.
где α – некоторая постоянная.
При выполнении условий 1 систему (1) заменим следующей эквивалентной системой с разделенными переменными [10, с. 8; 11, с. 115]:
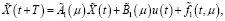 (4)
(4)
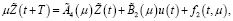 (5)
(5)
где 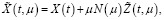
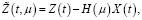 (6)
(6)
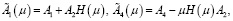
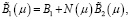
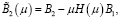
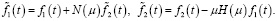
В соотношениях (6) матрицы H(μ), N(μ) имеют размерности m×n, n×m соответственно и удовлетворяют следующим уравнениям [10, с. 8]:
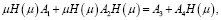 (7)
(7)
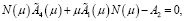 (8)
(8)
Уравнения (7), (8) имеют решения, которые могут быть представлены в виде равномерно сходящихся степенных рядов [10, с. 9]:
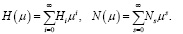 (9)
(9)
В [10, с. 9] определены матрицы Hi и Ns (i, s = 0, 1,…) путем приравнивания коэффициентов при одинаковых степенях μ в уравнениях (7), (8).
Начальные условия системы (4) и (5) определяются соотношениями
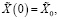
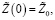 (10)
(10)
где 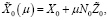
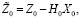
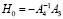 ,
, 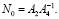 (11)
(11)
При μ = 0 из (6) будем иметь
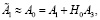
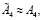
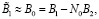
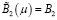 .
.
Предположим, что выполняется следующее условие.
Условие 2. Пусть A0 – устойчивая матрица, то есть собственные значения матрицы A0 удовлетворяют неравенству 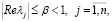 где β – некоторая постоянная.
где β – некоторая постоянная.
При выполнении условий 1 и 2 система (1) имеет интегральные многообразия [6, с. 17; 12, с. 772]:
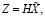
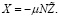 (12)
(12)
Интегральные многообразия (12) записываем в следующих формах:
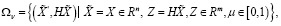 (13)
(13)
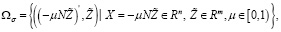
где 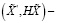 скалярные произведения векторов
скалярные произведения векторов 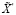 и
и 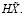
Матрицы B1 и B2 соответственно представим в следующих формах:

 (14)
(14)
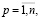
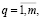
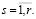
Тогда с учетом (6) и (14) имеем
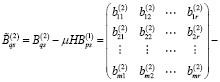
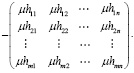
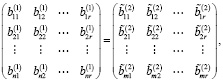
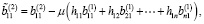
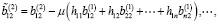
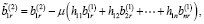
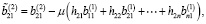
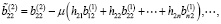
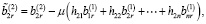
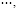
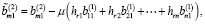
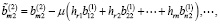
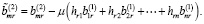
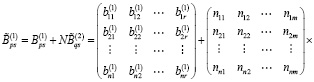




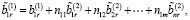
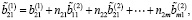
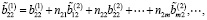
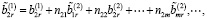
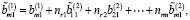
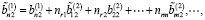
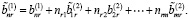
Предположим, что выполняются следующие условия:
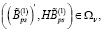
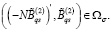 (15)
(15)
При выполнении условий (15) вместо исходной задачи (1)–(3) имеем задачу минимизации функционала (3) при ограничениях (4) и (5), при этом оптимальное управление u*(t) можно представить в форме [6, с. 18]:
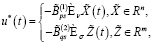 (16)
(16)
где 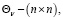
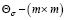 матрицы усиления, которые в процессе решения задачи определяются.
матрицы усиления, которые в процессе решения задачи определяются.
Таким образом, при выполнении условий 1, 2 и 15, задачу (1)–(3) представим в виде следующих двух подзадач, решения которых находится независимо друг от друга.
Задача A. Найти
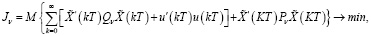 (17)
(17)
при ограничениях:
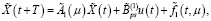 (18)
(18)
где 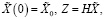
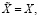
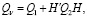
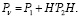
Известно [13, с. 463], что при заданном управлении справедливы следующие соотношения:
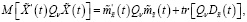
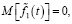 (19)
(19)
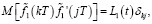
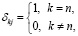
где математическое ожидание 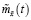 и ковариационная матрица
и ковариационная матрица 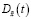 удовлетворяют следующим разностным уравнениям:
удовлетворяют следующим разностным уравнениям:
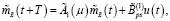
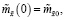 (20)
(20)
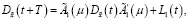
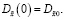 (21)
(21)
Задача B. Найти
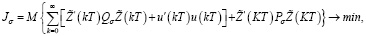 (22)
(22)
при ограничениях:
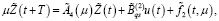 (23)
(23)
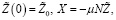
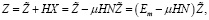 (24)
(24)
где 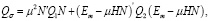
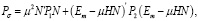
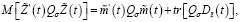
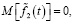
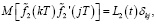
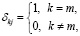
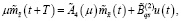
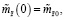 (25)
(25)
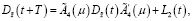
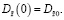 (26)
(26)
Решение задачи. Рассмотрим задачу A. Для определения оптимального управления задачи A используем метод Ляпунова [6, с. 18]. Для данных задач функции Ляпунова представим в виде
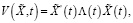
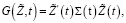 (27)
(27)
где Λ и Σ – положительно определенные матрицы. Тогда первые разности функции (27) соответственно можно записать в виде
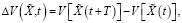 (28)
(28)
 (29)
(29)
Согласно методу Ляпунова первая разность функции Ляпунова должна быть отрицательна определенной. Объединив условие отрицательной определенности первой разности функции Ляпунова (27) с функционалом (17), полагаем
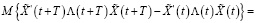
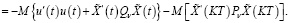 (30)
(30)
С учетом (16), (18) из (30) имеем
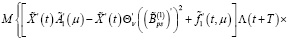
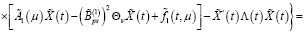
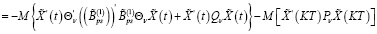
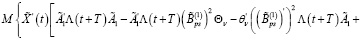
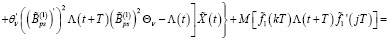
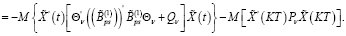
Из последнего равенства с учетом (19) получаем
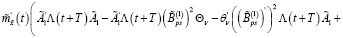
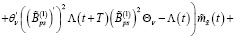
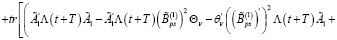
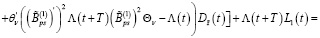
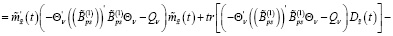
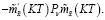 (31)
(31)
При выполнении условий 1, 2 и 15 решения уравнения (20), (21) существуют, также существуют: Θv – матрица усиления управляющей функции (16) и Λ(t) – матрица функции Ляпунова (27), как решения следующих алгебраических уравнений:
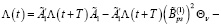
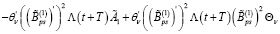 , (32)
, (32)
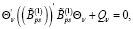
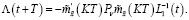
Тогда равенство (31) будет справедливым.
Теперь рассмотрим задачу B.
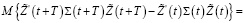
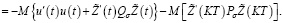 (33)
(33)
С учетом (16), (23) из (33) имеем
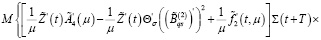
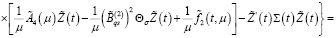
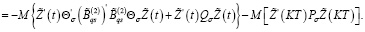
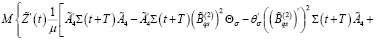
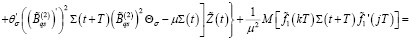
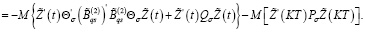
Из последнего равенства при любом 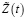 с учетом (24) получаем
с учетом (24) получаем
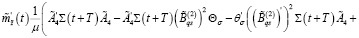
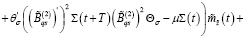
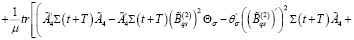
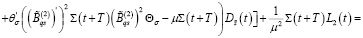
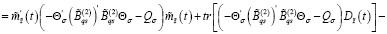
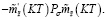 (34)
(34)
При выполнении условий 1, 2 и 15 решения уравнения (25), (26) существуют, также существуют: Θσ – матрица усиления управляющей функции (16) и Σ(t) – матрица функции Ляпунова (27), как решения следующих алгебраических уравнений:
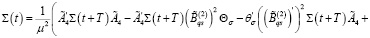
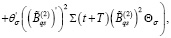 (35)
(35)
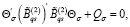
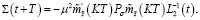
Тогда равенство (34) будет справедливым. Сформулируем следующее утверждение в виде теоремы, в которой содержатся основные результаты данной работы.
Теорема. Пусть выполняются условия 1, 2 и 15. Тогда в интегральных многообразиях (13) линейные дискретные регуляторы 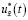 и
и 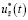 в виде обратной связи определяются соответственно функциями:
в виде обратной связи определяются соответственно функциями:
1) для задачи А:
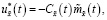 (36)
(36)
где 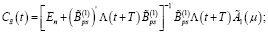
2) для задачи B:
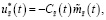 (37)
(37)
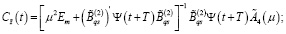
3) линейные дискретные регуляторы 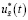 и
и 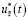 соответственно минимизируют функционалы (17), (22) и их минимальные значения определяются соотношениями
соответственно минимизируют функционалы (17), (22) и их минимальные значения определяются соотношениями
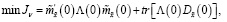 (38)
(38)
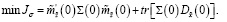 (39)
(39)
Доказательство. Докажем теорему для задачи A. Для того, чтобы минимизировать функционал (17), находим
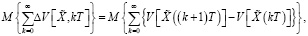 (40)
(40)
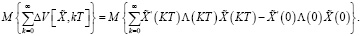 (41)
(41)
С учетом (17) и (19) из (40) имеем
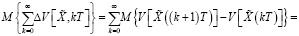
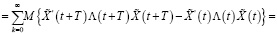
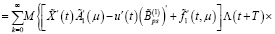
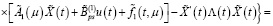
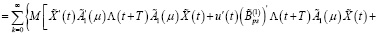
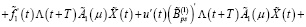
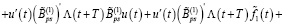
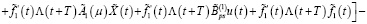
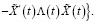
Теперь с учетом (19) из последнего равенства получаем
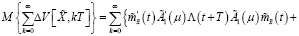
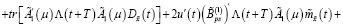
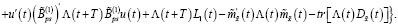 (42)
(42)
Сравнивая правые части выражений (41) и (42), получаем равенство
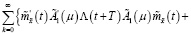
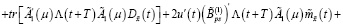
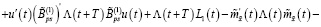
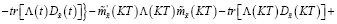
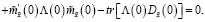 (43)
(43)
Функционал (17) с учетом (19) перепишем в виде
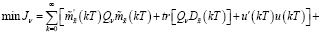
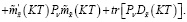 (44)
(44)
Теперь добавим к функционалу (44) левую часть равенства (43):
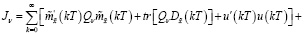
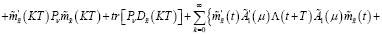
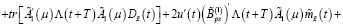
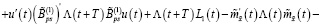
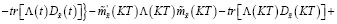
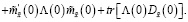 (45)
(45)
Оптимальный вектор u(t) должен удовлетворять условию 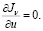 Тогда из (45) имеем
Тогда из (45) имеем
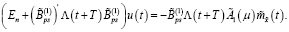
Из последнего равенства получаем линейный дискретный регулятор 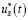 (36).
(36).
Доказательство, пункт 2. С учетом (16) из (45) имеем
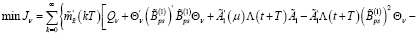
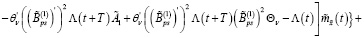
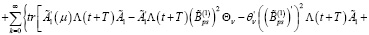
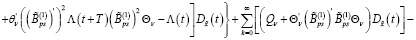
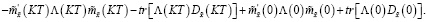
Из последнего равенства с учетом первого и второго уравнения (32) и считая что 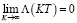 , получаем (38).
, получаем (38).
Доказательство теоремы для задачи B проводится аналогично задаче A.
Заключение
В работе для стационарной дискретной стохастической системы с разными темпами движений с использованием соотношений математических ожиданий, ковариационных матриц, матрицы усиления и функции Ляпунова случайных процессов, построен линейный дискретный регулятор, состоящий из двух линейных дискретных регуляторов, которые под их действием отдельно регулируются движения медленной и быстрой системы.
Результаты работы могут быть применены в исследовании дискретных стохастических задач оптимального управления, конструирования линейного регулятора для цифровой стохастической системы, а также в исследовании других постановок стохастических задач оптимального управления.



