Введение
Массовые мероприятия в настоящее время являются неотъемлемой частью современной жизни. С целью снижения риска возникновения чрезвычайных ситуаций при проведении таких мероприятий посетителям приходится входить через контрольно-пропускные системы, в частности турникеты. Грамотное планирование количества и места расположения таких систем позволяет повысить уровень удобства и безопасности и избежать больших очередей на входе в зону проведения мероприятия. С этой целью необходимо математическое моделирование потока посетителей, прибывающих к месту события.
В настоящее время существуют различные модели пешеходных потоков: микроскопические, мезоскопические и макроскопические [1, 2]. Каждая из них позволяет решать определенные задачи, использует различную степень детализации исходных данных.
Микроскопические модели требуют подробной детализации, учитывают поведение каждого человека и взаимодействие людей друг с другом. Макроскопические моделируют пешеходный поток в целом и оперируют такими данными, как скорость, плотность и интенсивность. Мезоскопическое моделирование сочетает микроскопические и макроскопические аспекты, то есть рассматривает отдельного человека с точки зрения всего потока.
Актуальной задачей является разработка теоретически обоснованных подходов выбора технических решений по установке контрольно-пропускных систем при проведении массовых мероприятий.
Целью исследования является разработка численных методов моделирования потока посетителей при проведении массовых мероприятий.
Материалы и методы исследования
При моделировании прохождения потока посетителей через контрольно-пропускную систему возможно применение теории массового обслуживания [3, с. 6]. С точки зрения приведенной выше классификации такие модели можно отнести к мезоскопическим. Теория массового обслуживания применяется для исследования процессов, протекающих в сложных стохастических системах.
Перед началом массового мероприятия в целях его безопасности посетители проходят через турникет. Образуется общая очередь у входа с n турникетами. То есть моделью прохода через турникет является многоканальная система массового обслуживания с неограниченной очередью. Время обслуживания можно считать распределенным по показательному закону. Однако поток заявок нельзя считать стационарным в данном случае. Согласно проведенным исследованиям [4, с. 44], интенсивность потока посетителей монотонно возрастает от нуля до некоторого максимума. Максимум достигается за 10–15 минут до начала события. Затем снижается до нуля.
Для моделирования системы массового обслуживания (СМО) с переменной интенсивностью входящих потоков в ряде работ [4, с. 50] предлагается применять аппроксимацию интенсивности входящего потока с помощью кусочно-непрерывных функций. В этом случае можно представить работу нестационарной СМО как последовательную работу стационарных СМО, каждая из которых подключается в тот момент, когда окончена работа другой. Изменяться будут начальные условия, то есть значения вероятностей пребывания системы в определенном состоянии.
Наиболее важными характеристиками, которые требуется получить, являются следующие: максимальная длина очереди; максимальная длительность ожидания в ней; периоды времени, в которые длина очереди достигает максимальной длины и время ожидания оказывается максимальным; число обслуженных к моменту начала массового мероприятия заявок; время, затраченное на обслуживание всех поступивших аявок.
Результаты исследования и их обсуждение
1. Составление системы дифференциальных уравнений для вероятностей состояний
Моделью похождения людей через турникет при входе на мероприятие можно считать СМО вида Ek / M / m / n. То есть входящий поток заявок (поток посетителей, подходящих ко входу на мероприятие) – это поток Пальма с распределением интервалов по времени между подряд идущими событиями по закону Эрланга порядка k. Обслуживание заявок (проход через турникет одного посетителя) распределено по показательному закону. Имеется m турникетов (обслуживающих приборов). Место в очереди ограничено (можно принять n = 100 – 150.
Составим систему дифференциальных уравнений для состояний системы. Обозначим Um состояние, при котором в системе находится m требований. Для марковизации процесса будем использовать метод псевдосостояний [5, с. 214]. Входящий поток специального распределения Эрланга можно представить в виде суммы k показательных распределений с параметром λ.
Рис. 1. Псевдосостояния распределения Эрланга порядка k
Псевдосостояния для Um изображены на рис. 1.
Составим дифференциальные уравнения для нахождения вероятностей пребывания системы в состояниях Um [6, c. 56]. Граф состояний изображен на рис. 2.
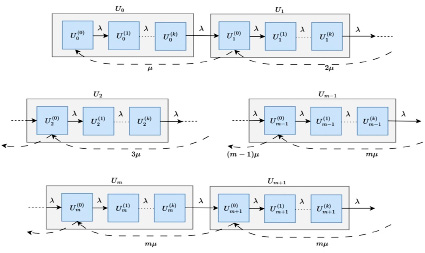
Рис. 2. Граф состояний СМО Ek / M / m / n
В дальнейшем будем обозначать ps(0) = ps для всех s.
1) Um+i все каналы заняты, i требований в очереди.
Обозначим Pn+i (t +∆t) – вероятность нахождения в очереди i требований в момент (t +∆t).
Pn+i (t + ∆t) ≈ P(A) + P(B) + P(C), (1)
где А = {система была в состоянии (m + i), и ничего не случилось за время ∆t};
В = {система была в состоянии (m + i – 1), и пришло очередное требование за время ∆t};
С = {система была в состоянии (m + i – 1), и за время ∆t освободился один из каналов обслуживания}.
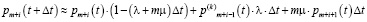. (2)
Разделим на ∆t:
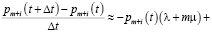
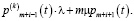(3)
При ∆t → 0 получим систему дифференциальных уравнений:
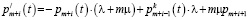, (i = 1, 2, … ,n – 1). (4)
2) Us – нет очереди и заняты s (s ≤ m) каналов обслуживания
Ps(t + ∆t) – вероятность нахождения системы в этом состоянии. Система будет находиться в состоянии Us если произойдут следующие события:
А = {за время ∆t не прибыло ни одно требование и не освободился ни один из m каналов обслуживания};
B = {освободился один из (s + 1)-го занятого канала обслуживания};
C = {в момент t были заняты (s – 1) канал обслуживания, и за время ∆t прибыло одно требование}.
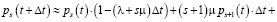
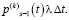(5)
Отсюда получаем дифференциальное уравнение:
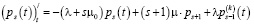(s = 1, 2, … ,m). (6)
3) U0 – система полностью свободна.
Аналогично предыдущему, получается уравнение
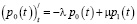. (7)
4) Um+n – все каналы заняты, в очереди n заявок.
Псевдосостояние Um+n состоит из одного подмножества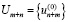 
.
Для вероятности pm+n(t +∆t) получаем уравнение
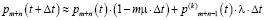. (8)
Отсюда
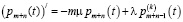. (9)
5) нахождение в псевдосостоянии Us
Для вероятностей ps(j)(t) пребывания в транзитивных состояниях us(j) справедливо
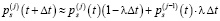. (10)
Разделим на ∆t и найдем предел при ∆t → 0:
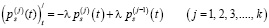. (11)
Итак, для определения неизвестных вероятностей получаем систему дифференциальных уравнений:
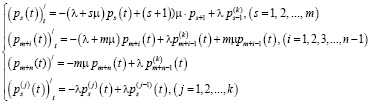. (12)
2. Представление переменной интенсивности в виде кусочно-стационарной функции
Для моделирования нестационарного потока посетителей в случае, когда интенсивность потока меняется с течением времени, представим его в виде куочно-непрерывной функции. Для этого разобъем всю временную ось на интервалы [ti–1; ti]. И будем считать на каждом из них интенсивность поступления заявок постоянной. В этом случае стационарными будут и значения параметров Эрланга на каждом таком интервале. Для i-го интервала обозначим их λi и ki.
Тогда с помощью функции Хэвисайда можно записать зависимость параметров распределения от времени следующим образом:
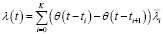, (13)
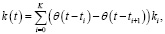(14)
где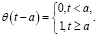 
Тогда для вычисления характеристик качества функционирования СМО применяются формулы
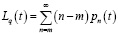– зависимость длины очереди от времени;
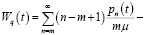зависимость ожидания в очереди от времени.
Таким образом, для решения поставленной задачи надо решить систему дифференциальных уравнений Колмогорова для стационарной СМО при произвольных начальных условиях и записать вероятности pn(t) через функцию Хэвисайда.
Для определения неизвестных вероятностей СМО на каждом из интервалов [ti–1; ti] требуется решить систему дифференциальных уравнений (12). Начальные условия имеют вид
pg(0)(0) = 1, pm(j) = 0 (m = 0, 1, 2, ..., g–1, g+1, , …; j = 1,…, k, j = 1,2,3,…, q). (15)
Номер g вероятности pg(0)(0), отличной от нуля в начале нового временного интервала [ti–1; ti], определяется из условия g = [M(X(t))] – целая часть от математического ожидания числа заявок X(t) в системе на предыдущем временном интервале [ti–2; ti–1].
Следует учитывать, что
1) в наших обозначениях pm(0) = pm для всех m;
2) rm(t) = P(Um), то есть rm(t) – вероятность пребывания системы в состоянии Um ;
3) согласно законам теории вероятностей: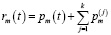 
.
3. Численное решение системы дифференциальных уравнений
Возможны различные численные решения [7] полученной системы дифференциальных уравнений (12).
1 способ. Решить систему линейных дифференциальных уравнений (12) можно, например, методом Эйлера. Введем следующие обозначения:
,
,
,
.
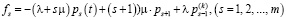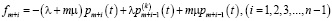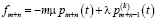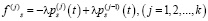Расчетные формулы будут иметь вид
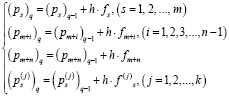(16)
pg(0)(0) = 1, ps(j) = 0 (s = 0, 1, 2, .., g–1, g+1, , …; j = 1,…, k, j = 1,2,3,…, q)
где h – шаг интегрирования, s – номер итерации.
Или методом Рунге – Кутты, например, четвертого порядка:
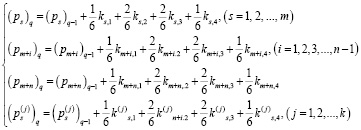. (17)
Здесь используются следующие обозначения для l = 0,1,…,m+n:
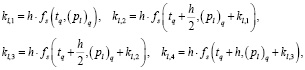(18)
А также
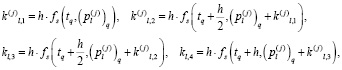(19)
Этот метод на каждом шаге требует четырех вычислений правой части дифференциального уравнения. Но так как он четвертого порядка, то приводит к уменьшению вычислительной погрешности.
2 способ. Численно-аналитический метод решения системы линейных дифференциальных уравнений.
Система линейных однородных дифференциальных уравнений (12) в матричном виде примет вид
P(t) = A ∙ P(t). (20)
Причем матрица А – трехдиагональная. Для трехдиагональной матрицы можно найти собственные значения, используя стандартный алгоритм:
1 шаг: находим характеристический многочлен det(A – λE) = 0
Для трехдиагональной матрицы существует специальный способ вычисления определителя det(A – λE) без явного выражения в виде многочлена.
Пусть Dm(λ) – главный минор m-го порядка матрицы (A – λE). Тогда:
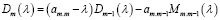– разложение минора по последней строке.
Дополнительный минор Mm.m–1(λ) для элемента am.m–1 в последнем столбце содержит один ненулевой элемент a m–1.m. Поэтому его можно разложить по этому столбцу:
.
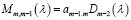Итак, получаем рекуррентную формулу для вычисления миноров:
, 
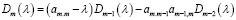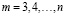. (21)
2 шаг: находим корни характеристического многочлена.
Корни многочлена Dn(λ) можно найти, например, методом парабол.
3 шаг: выписываем решение системы, используя аналитический подход для систем обыкновенных дифференциальных уравнений.
Следует отметить, что нахождение решения системы (12) в данном случае, в отличие от численного метода, дающего конечный набор точек, представляет собой построение процедуры, позволяющей определить вероятности состояний в произвольный момент времени [7].
Заключение
Анализ опыта организаций масштабных массовых мероприятий показывает огромную значимость грамотной организации управления потоками посетителей. Для эффективного использования контрольно-пропускной системы необходимо установить соответствие между параметрами системы и характеристиками пешеходного потока. Один из методов, который позволяет это сделать, рассмотрен в данной работе. В силу большой размерности системы, возможно только численное ее решение. С этой целью приведены два различных способа ее решения.