Введение
Одним из ключевых аспектов, определяющих успешность сельскохозяйственного производства, является равномерное распределение растений на площади питания. Этот фактор во многом зависит от качества посева, которое, в свою очередь, определяется характеристиками высевающего устройства.
Изучение текущих высевающих технологий и устройств дало возможность определить многообещающее направление – создание роторно-лопастных машин для принудительного распределения семян. Эти аппараты обладают способностью обеспечивать точный контроль за дозировкой семенного материала, учитывая его физико-механические характеристики.
Целью исследования является создание теоретической модели процесса посева семян, в котором используется лопастное дозирующее устройство. Основное внимание уделяется анализу движения семенного материала и определению мгновенной подачи лопастного дозирующего устройства при бесконечно малом изменении угла поворота лопасти в стабильном режиме работы.
Материалы и методы исследования
В Самарской государственной сельскохозяйственной академии на кафедре «Механика и инженерная графика» ведется разработка лопастного устройства, предназначенного для дозирования семенного материала. Исследуемый прототип данного устройства обеспечивает стабилизацию потока семян перед их попаданием в высевное окно, что способствует равномерному распределению семян (рис. 1). Прототип устройства состоит из следующих элементов: резервуар 1, корпус 2, оснащенный высевным окном 8, ротор 3, а также торсионные втулки 5, оснащенные плоскими лопастями 4, расположенными под определенным углом атаки α. Эти лопасти являются основой предлагаемого дозатора. На передней стенке 6 корпуса 2 расположено высевное окно 8, оснащенное заслонкой 7. Между передними плоскими лопастями 4 и стенкой 6 корпуса образуется стабилизационная камера 9.
Роторно-лопастной дозатор функционирует по следующему принципу. В процессе вращения ротора 3 плоские лопасти 4 захватывают семена из семенного резервуара 1 и направляют их в стабилизационную камеру 9. В этой камере семена равномерно распределяются и образуют слой определенной толщины. Благодаря этому давление на лопасти уменьшается, и они начинают поворачиваться, уменьшая угол атаки α. Это позволяет лопастям мягко перемещать семена к высевному окну 8.
Заслонка 7 на высевном окне регулирует количество подаваемых семян, обеспечивая необходимую норму высева. Таким образом, роторно-лопастной дозатор обеспечивает равномерное распределение семян с учетом их размера, формы и плотности, что способствует увеличению урожайности и снижению затрат на посевные работы [1–3].
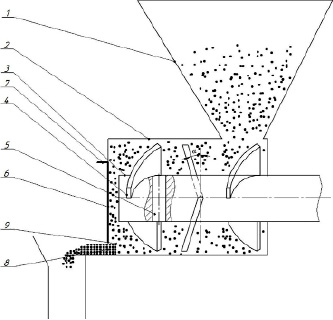
Рис. 1. Схема роторно-лопастного дозатора
Результаты исследования и их обсуждение
Для исследования движения семенного материала авторы рассчитывают мгновенную подачу роторно-лопастного дозатора при небольшом изменении угла поворота лопасти в установленном режиме работы. Предполагается, что движение слоя семян будет равномерным и соответствовать законам движения единичного объема.
Рассмотрим проекцию лопасти на плоскость, перпендикулярную оси ротора. Выделим лопасти элементарную площадку бесконечно малой величины (рис. 2), равную [4–6]:
dSл = RdRdε, (1)
где R – внутренний радиус элементарной площадки, м; dR – ширина элементарной площадки, м; dε – угол сегмента элементарной площадки, град.
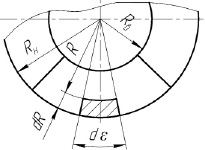
Рис. 2. Развертка лопасти
Для вычисления подачи материала плоской лопастью можно применить следующее уравнение:
dQл = υ1 ∙ dSл , (2)
где υ1 – осевая скорость перемещения семенного материала, м/с.
После интегрирования уравнения (1)
Sл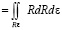 
получим, что площадь поверхности перемещающей материал лопасти равна (без учета технологических зазоров) [7–9]:
Sл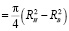 
, (3)
где RH – наружный радиус лопасти, м; RB – внутренний радиус лопасти, м.
Далее для решения теоретического вопроса о взаимодействии вращающейся лопасти и перемещаемой ею частицы высеваемого материала воспользуемся уравнением Лагранжа [10–12].
Из-за неидеальности связей пара сил трения выражается между стенкой корпуса F1 и поверхностью лопасти F2.
Существует такое понятие, как обобщенная координата, в рассматриваемом случае такой является s, и относительно нее уравнение Лагранжа второго рода запишется
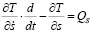, (4)
где T – кинетическая энергия частицы высеваемого материала, Дж; t – время движения частицы, с; Qs – обобщенная сила, соответствующая обобщенной координате s, Н.
Определим Qs, для чего вычислим сумму работ, выполненных активной силой и силами сопротивления при перемещении δs [13–15]:
∑δA(Fk ) = (∑Fks )δs, (5)
где ∑δA(Fk) – общая сумма работ активной силы и сил трения, Дж; ∑Fks – сумма сил по направлению перемещения частицы на поверхности лопасти S (рис. 3).
Для понимания направления действующих сил на частицу, находящуюся на поверхности лопасти, развернем винтовую линию движения частицы, так чтобы плоскость была касательной к образующей поверхности корпуса (рис. 3).
Реакция F1 (рис. 3) вектор, которой направлен в обратную сторону от перемещения частицы и действует в направлении υ0, отсюда
F1 = N1 ∙ f1, (6)
где N1 – действующая реакция силы на частицу материала, направленная с поверхности лопасти, которая образует угол α с осью Oz, Н; f1 – коэффициент трения частицы о поверхность лопасти.
При этом сила трения,
F2 = N2 ∙ f2,
направлена обратно вектору абсолютной скорости, где N2 – реакция на частицу перемещаемого материала с внутренней поверхности кожуха, Н; f2 – коэффициент трения частицы о внутреннюю поверхность корпуса.
Представим, что Qs, обобщенная сила реакций, будет коэффициентом при δs в выражении (5):
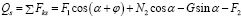, (7)
где φ – угол между векторами скорости частицы υ и ее горизонтальной составляющей υe , град.; G – сила тяжести, Н.
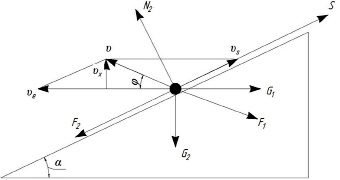
Рис. 3. Разложение векторов по винтовой линии на плоскость
С учетом выражения (7) запишем уравнения для сил трения следующим образом:
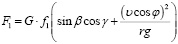, (8)
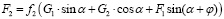, (9)
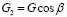
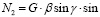, (10)
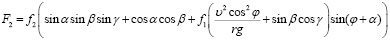, (11)
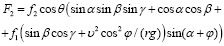, (12)
где r – переменный радиус вращения частицы указывает на то, что расстояние от центра вращения и направление движения изменяются в зависимости от времени. Это вызывает движение частицы по криволинейной траектории, м.
Определим угол поворота γ, то есть на сколько градусов повернется материальная точка в плоскости перпендикулярной оси вращения лопастей за определенный промежуток времени t, при этом необходимо учитывать, что частица перемещается с координатой s [16].
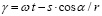. (13)
Значения cos(α + φ), sin(α + φ) выразим через переносную координату:
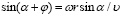. (14)
Применяя теорему косинусов, получим
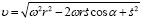, (15)
где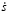 
– первая производная от перемещения частицы, м/с.
Тогда, с учетом выражения (15),
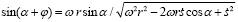, (16)
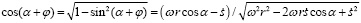. (17)
Скорость вращения частицы получит выражение
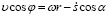. (18)
Подставив (8), (10), (12) при этом учитывая (13), (15), (17), (18) подставив в (7), получим
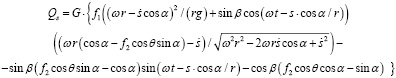. (19)
Поскольку частица находится в постоянном движении, определим ее кинетическую энергию:
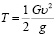. (20)
После подстановки выражения (15) в (20), получим
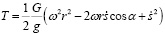. (21)
Чтобы найти производные этих функций, воспользуемся формулой (1). Затем вычислим значения производных:
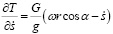, (22)
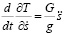, (23)
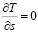. (24)
После замены выражения Qs из (19) и производных (23) и (24) в уравнении Лагранжа (4) и упрощения, авторы пришли к дифференциальному уравнению движения частицы:
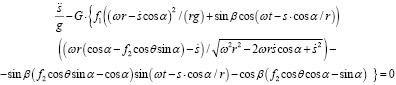. (25)
Уравнение (25) отражает движение частицы относительно высевающего устройства. В процессе анализа выявлено, что перемещение частицы высевающего материала, в кожухе цилиндрического сечения, при перемещении лопастями. При этом зная, что частица в момент переноса к окну высева перемещается внутри корпуса в различных направлениях, получим, что коэффициенты трения частицы f1 = 0,5 – о поверхность лопатки, f2 = 0,5 – о внутреннюю поверхность корпуса; H = 0,025 м – шаг винтовой линии; ω = 3 с−1 – угловая скорость вращения; r = 0,02 м – внутренний радиус корпуса устройства. На основе полученных результатов был построен рисунок 4.
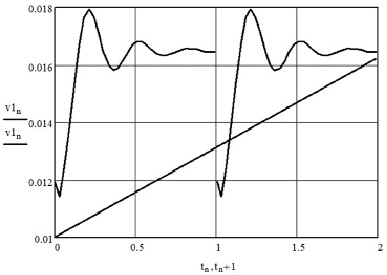
Рис. 4. Осевая скорость частицы материала определяется временем и заданными характеристиками
Участки неустановившегося движения частицы для заданных условий расчета в основном зависят от скорости вращения лопаток дозатора. Под воздействием первого ряда лопаток из семенного бункера частица начинает перемещаться в цилиндрическом корпусе с периодически изменяющейся осевой скоростью. Характер затухающих колебаний осевой скорости представлен на рис. 4. Далее частица захватывается последующим рядом лопастей лопаток и продолжает перемещаться с периодически изменяющейся осевой скоростью. Затухающие колебания переходят в движение частицы с постоянной осевой скоростью, зависящей от угловой скорости вращения ротора дозатора.
Практическая значимость разработки роторно-лопастного дозатора для высева семян заключается в возможности его применения в сельском хозяйстве для точного и равномерного распределения семян по почве. Это способствует повышению урожайности и качества посевов, снижению затрат на посевную кампанию и улучшению условий труда аграриев.
Кроме того, разработка может быть интересна производителям сельскохозяйственной техники, научных учреждений и организаций, занимающихся вопросами сельского хозяйства.
Заключение
В процессе теоретических исследований и обработки информации было выведено дифференциальное уравнение, описывающее перемещение частицы в сеялке. Это уравнение было получено с помощью преобразования уравнения Лагранжа. Решение этого уравнения позволило определить характер и скорость осевого перемещения частицы материала в устройстве высева, которое в начальный момент времени не стабильно и изменяется в пределах от 0,011 до 0,018 м/c. При этом через полсекунды перемещение стабилизируется, и средняя скорость перемещения частиц составляет 0,013 м/c, что согласуется с экспериментальными значениями подачи материала в пределах от 2 до 5 г/с в зависимости от частоты вращения лопаток.