Введение
При проведении масштабных культурно-массовых мероприятий значительно увеличивается плотность пешеходных и транспортных потоков в зоне их проведения. Возможность предсказывать эти изменения позволяет качественно организовать дорожное движение на этот период, минимизировать вероятности возникновения заторов, повысить уровень удобства для посетителей мероприятия [1]. Важную роль играет моделирование пешеходных потоков в различных ситуациях, возникающих при проведении массовых мероприятий. Особенно трудно контролировать поведение пешеходов в случае паники. Во избежание таких ситуаций организаторам требуется грамотное планирование и подробное изучение особенностей поведения посетителей [2] с целью прогнозирования следующих параметров:
– время эвакуации зрителей в различных зонах разграничений;
– расположение, количество и характеристики эвакуационных выходов;
– пропускная способность в местах пересечений пешеходных и транспортных потоков.
При этом управляемыми параметрами могут быть время обслуживания, время ожидания в местах входа-выхода посетителей (системах массового обслуживания), количество таких систем обслуживания на пути следования, наполняемость накопителей.
Существуют различные виды моделей пешеходных потоков. В общем случае они аналогичны моделям транспортных потоков и делятся на макроскопические, мезоскопические и микроскопические [3; 4]. Макроскопические модели исследуют общие характеристики потока, представляя его как поток жидкости. Микроскопические уделяют внимание поведению отдельного пешехода и его взаимодействию с остальными участниками движения. Некоторый средний между этими методами моделирования уровень представляют мезоскопические модели [5, c. 19].
Актуальной задачей является разработка математической модели потока пешеходов при прохождении через «узкое место», в частности при выходе из зоны проведения массовых мероприятий, позволяющей с достаточной степенью точности предсказывать параметры пешеходных потоков и качество организации их движения.
Целью исследования является повышение уровня обслуживания посетителей при проведении масштабных массовых мероприятий.
Материал и методы исследования
Место проведения мероприятия разделяют на площадку и район мероприятия. Площадкой может быть, например, стадион или концертный зал. Площадка мероприятия состоит из зоны проведения самого мероприятия с выходами и канализированием пешеходных потоков. Районом мероприятия или зоной «последней мили» считается прилегающая территория и улично-дорожная сеть в радиусе около 1500 метров от «площадки».
Значительно снизить риски, связанные с возникновением нештатных ситуаций при проведении массовых мероприятий, возможно с помощью информационных контрольно-пропускных систем [6]. Их стуктура должна соответствовать особенностям мероприятия и места его проведения.
Информационно-пропускные системы позволяют управлять движением потоков посетителей с помощью, например, указания направления движения пешеходных потоков на информационном табло. В частности, при критической плотности потока в одном направлении изменять указания по возможному движению потока.
Модель движения пешеходов при прохождении через контрольно-пропускной пункт может быть описана с помощью систем массового обслуживания [7, с. 23], что позволяет получить характеристики очереди при выходе из зоны проведения мероприятия. Плотность пешеходного потока в этом случае высокая и, согласно различным исследованиям, она согласуется с нормальным распределением. Нормальный закон аппроксимируется в свою очередь законом Эрланга [8, c. 70] порядка не ниже пятого, который позволяет моделировать системы массового обслуживания различной сложности.
Результаты исследования и их обсуждение
1. Модель пешеходного потока при выходе с площадки мероприятия
Рассмотрим пешеходные потоки при выходе с площадки мероприятия и прохождении через узкие двери (через «бутылочное горло»).
В этом случае пешеходы двигаются прямолинейно в b рядов: b1 с одной стороны и b2 с другой. Потоки сливаются перед дверным проемом, в котором могут одновременно поместиться m человек.
Можем считать это системой массового обслуживания с ожиданием с m каналами обслуживания. Так как потоки в этом случае высокой плотности, то согласно проведенным исследованиям можно считать, что интервалы по времени между подряд идущими пешеходами распределены по нормальному закону. А также поток быстро переходит в стационарное состояние.
Под временем обслуживания будем понимать время прохода через «узкое место» (двери) одним человеком. В описываемой ситуации это время тоже можно считать распределенным по нормальному закону.
Нормальный закон хорошо аппроксимируется законом Эрланга при значении параметра k ≥ 5 (рис. 1).
Итак, имеется m каналов обслуживания, очередь можно считать ограниченной, в ней могут находиться не более n человек. Поток заявок имеет распределение Эрланга порядка k. Время обслуживания имеет распределение Эрланга порядка l. Таким образом, имеем систему массового обслуживания вида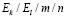 
.
В этом случае с помощью метода псевдосостояний [9, с. 18] можно свести систему к Марковскому процессу.
Закон Эрланга порядка k можно представить как сумму k одинаковых показательных распределений (этапов, фаз или псевдосостояний).
a)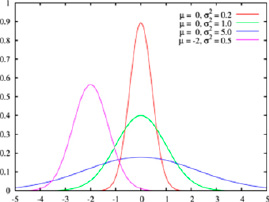 
б)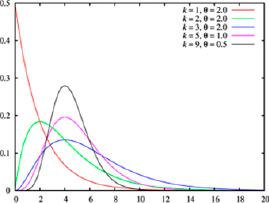 
Рис. 1. Виды распределения потоков: а) нормальное распределение (распределение Гаусса); б) гамма-распределение (распределение Эрланга)
Для удобства составления матриц интенсивностей процесса введем следующую нумерацию псевдосостояний:
1) для входящего потока (закон Эрланга Ek порядка k с интенсивностью λ) псевдосостояние номер 1 совпадает с поступлением предыдущей заявки, псевдосостояние номер k – с поступлением текущей заявки;
2) для процесса обслуживания (закон Эрланга El порядка l с интенсивностью μ) псевдосостояние номер l совпадает с поступлением заявки на обслуживание, псевдосостояние номер 1 – с окончанием обслуживания.
Пример графа состояний для СМО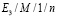 
, СМО 
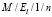и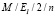 
приведен на рис. 2.
2. Математические объекты и обозначения при моделировании системы массового обслуживания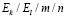 
Введем обозначения:
Ur – множество всех микросостояний, в котором в системе находится r заявок;
Ω = {1,2,…,ω} , ω ≤ ∞:
,
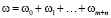где ωq – число состояний на уровне Uq ;
(i,j,r) – псевдосостояние СМО, в котором i – номер этапа входящего потока, j – этап обслуживания, r – число требований в системе;
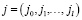– состояние приборов на обслуживании, где j0 – число свободных приборов, jq – число приборов на этапе обслуживания номер q, при этом q ≤ l, 0 ≤ jq ≤ m и 
.
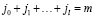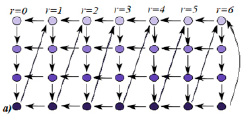
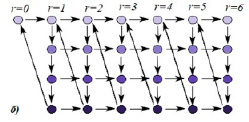
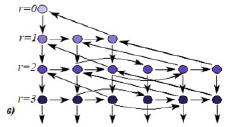
Рис. 2. Пример графа состояний: а) СМО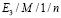 
; б) СМО 
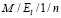; в)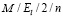 
Будем считать, что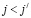 
, если
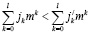
Для составления матриц необходимо упорядочить состояния.
Пусть N(i,j,r) – номер псевдосостояния СМО. Будем считать, что:
1) если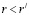 
, то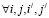 
верно: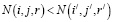 
2) если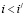 
, то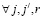 
верно: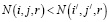 
3) если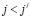 
, то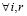 
верно: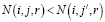 
Пусть множество Ω представлено в виде: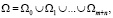 
причем 
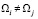при i ≠ j.
А также если i < j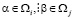 
, тогда α < β.
Обозначим pNl,Nm (t) – вероятность того, что система перейдет из состояния Nl в состояние Nm за время t.
Можно считать, что существует стационарное распределение,
,
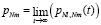где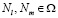 
и 
.
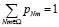Обозначим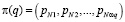 
– вектор стационарных вероятностей подмножества Uq.
P(t) – матрица вероятностей одношаговых переходов.
Q – матрица, состоящая из интенсивностей перехода из состояния Nl в состояние Nm.
Элементы матрицы Q следующие:
,
.
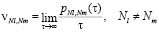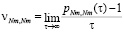Справедливо соотношение:
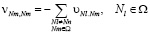
Для удобства записи уравнений состояний СМО разобьем матрицу Q на следующие блоки:
Qαβ – прямоугольная матрица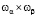 
, состоящая из интенсивностей перехода из состояния 
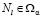в состояние 
.
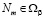При выбранной нумерации в матрицах Qαβ элементы над главной диагональю зависят только от параметров входящего потока, а элементы под главной диагональю – от характеристик обслуживания.
Уравнения равновесия системы следующие:
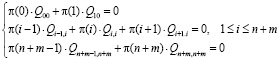(1)
3. Метод построения элементов матрицы Qαβ
1. Элементы блоков Qr,r+1 соответствуют переходам из псевдосостояния (i,j,r) уровня Ur в псевдосостояние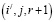 
уровня Ur+1. Все элементы нулевые, кроме элементов при 
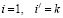(для входящего потока Ek ), которые равны kλ.
2. Элементы блоков Qr,r–1 соответствуют переходам из псевдосостояния (i,j,r) уровня Ur в псевдосостояние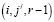 
уровня Ur–1. Ненулевыми элементы блока (при обслуживании El) будут при выполнении следующих условий:
,
,
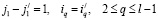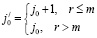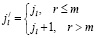. (2)
Равны они соответственно (j1,lμ).
3. Блоки Qr,r квадратные. Элементы, стоящие под главной диагональю, будут ненулевыми только при условии, что для j и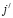 
существует единственный индекс q, 0 ≤ q ≤ l, такой, что 
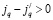, для остальных индексов 
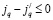. Соответствующие элементы равны (jq,lμ). Остальные элементы под главной диагональю равны нулю. Эти элементы характеризуют переход из (i,j,r) в 
.
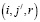Элементы, стоящие над главной диагональю, будут ненулевыми только при условии, что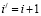 
. Равны они соответственно (kλ). Остальные элементы над главной диагональю равны нулю. Эти элементы характеризуют переход из (i,j,r) в 
.
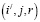4. Алгоритм вычисления стационарных вероятностей СМО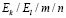 
:
1) определить множество состояний СМО Ω = {(i,j,r)} и его уровни Ur;
2) определить блоки Qαβ, составляющие матрицу Q интенсивностей переходов;
3) найти решение системы (1) с помощью рекуррентных соотношений:
3.1) найти матрицы Di, 1 ≤ i ≤ n:
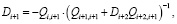
Dn+1 = 0
3.2) найти π(0) из системы уравнений:
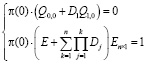, (3)
где E – единичная матрица, En×1 – столбец из единиц.
3.3) найти π(i), 1 ≤ i ≤ n, используя рекуррентное соотношение:
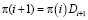
5. Вычисление характеристик пешеходного потока при выходе из зоны проведения мероприятий.
После определения стационарных вероятностей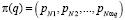 
на уровне Uq появляется возможность определения характеристик системы. Обозначим сумму стационарных вероятностей на уровне Uq как π(q)Σ.
Tогда:
1) среднее число требований в очереди:
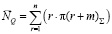
2) среднее число заявок в системе:
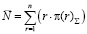
3) среднее время ожидания в очереди:
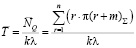
Заключение
При проведении масштабных массовых мероприятий неотъемлемой частью является качественный и количественный анализ потоков посетителей. В связи с этим актуальной задачей является математическое моделирование ситуаций, возникающих в зоне проведения мероприятия. В данной работе приведен метод моделирования пешеходного потока при выходе из зоны проведения массовых мероприятий, который можно отнести к классу мезоскопического моделирования. Метод позволяет рассчитывать характеристики качества организации обслуживания участников мероприятия и может быть использован при автоматизированном регулировании потоков посетителей с помощью информационного табло.