Введение
Математическая грамотность является неотъемлемым аспектом функциональной грамотности и проявляется в способности использовать математические методы для решения задач в различных контекстах, выходящих за рамки чисто математических ситуаций. Ключевым навыком в этом процессе становится возможность структурировать проблему на языке математики, корректно применять математические термины и интерпретировать результаты, что и служит показателем развития функциональной математической грамотности.
Наиболее значимым ключевым фактором обучения является умение применять усвоенные знания и навыки в различных ситуациях, как в повседневной жизни, в учебной среде, так и в профессиональной деятельности. Обратим внимание на то, что функциональная грамотность является главным инструментом для успешной адаптации и достижения успеха в современном обществе, позволяет не только понимать информацию, но и уметь применять ее на практике, решая конкретные задачи и достижения поставленных целей. Развитие функциональной грамотности является неотъемлемой частью обучения, способствуя формированию универсальных навыков и качеств, необходимых для реализации своих потенциальных возможностей.
Математическая грамотность является главной составляющей функциональной грамотности. Как правило, для достижения высокого уровня понимания и применения математических данных в различных ситуациях необходимо продолжать развивать и углублять навыки математической грамотности.
В контексте современных образовательных трендов такие методы, как проектное обучение, проблемно-ориентированное обучение и кейс-метод, активно включают элементы функциональной грамотности, предоставляя студентам возможности для развития умений, необходимых для решения практических задач [1, 2]. Это подходы, позволяющие углублять знания через активное применение теоретического материала в условиях, приближенных к реальным.
Исследования И.И. Валеева [3], Г.А. Симоновской [4] освещают процесс формирования и оценки математической грамотности, подчеркивая ее значимость для развития интеллектуальных способностей, социальной адаптации и профессиональных навыков учащихся. Особое внимание в работах уделяется влиянию математической грамотности на общий образовательный и социальный успех учеников.
Работа А.В. Боровских представляет собой анализ математической грамотности с акцентом на значении знаковых систем, которые играют важную роль в понимании и овладении этой компетенцией [5]. В исследовании освещены методические аспекты, связанные с определением, принципами и особенностями применения математической грамотности в образовательном процессе.
В эпоху развития информационных технологий значимость математической грамотности находит подробное освещение в работах таких ученых, как С.И. Калинин, С.И. Торопова и Ю.И. Макарова [6]. Авторы утверждают, что грамотность критически необходима для успешной адаптации к изменчивым условиям информационного мира, выступая ключевым инструментом для ориентирования в сложившихся реалиях. Результаты исследования показывают, что освоение математической грамотности обеспечивает человеку возможность адекватно реагировать на требования современности и эффективно взаимодействовать в быстро меняющемся мире.
Функциональная грамотность становится ключевым элементом в структуре современного образования, отражая необходимость в подготовке молодежи к эффективной адаптации к вызовам времени, стимулированию инновационной активности и поддержанию процесса постоянного самообразования [7, 8]. Это направление демонстрирует стремление образовательных систем к переосмыслению своих подходов в ответ на динамично меняющуюся информационную среду, выделяя необходимость воспитания у студентов готовности к активному взаимодействию с социальной средой.
Внедрение инновационных образовательных методик, фокусирующихся на использовании знаковых систем, значительно усиливает интерес к математике и способствует развитию умений, необходимых для решения практических задач. Такой подход подчеркивает критическую роль математики в обучении, поскольку он способствует не только освоению математических навыков, но и формированию критического мышления, аналитических способностей и умения применять математические знания в разнообразных жизненных ситуациях [9].
Концептуальные разработки в области оценки математической грамотности открывают новые перспективы для углубления в методы диагностики и улучшения образовательных результатов. Эти подходы позволяют образовательной системе и преподавателям выявлять и анализировать проблемы в учебном процессе, а также разрабатывать стратегии для оптимизации процесса обучения [10].
Исследования, затрагивающие преподавание математики в контексте жизненных ситуаций, демонстрируют значимость практического применения учебных знаний. Привлечение студентов к реальным задачам делает математическую грамотность более понятной и доступной для учащихся.
Научные работы часто описывают функциональную грамотность как критически важный элемент в адаптации к социальным контекстам. Это проявляется в способности к эффективному взаимодействию с изменениями в окружающем мире, умении решать нестандартные задачи и установлении социальных связей.
Активное вовлечение студентов в решение прикладных задач улучшает понимание математической грамотности, делая ее не только актуальной, но и глубже осмысленной в их учебном процессе. В работе [11] функциональная грамотность описана как важный элемент успешной социальной адаптации, включающий возможности адаптации к изменениям, решения нетрадиционных задач и построения социальных связей.
Универсальные компетенции, связанные с развитием функциональной грамотности, включают анализ информации, формулирование целей и разработку стратегий их достижения. Они также акцентируют важность умения структурировать устную и письменную речь, что необходимо для профессиональной деятельности.
Целью настоящего исследования являлось формирование и развитие функциональной математической грамотности у студентов первых курсов гуманитарных направлений в Кабардино-Балкарском государственном университете (КБГУ).
Исследование направлено на определение и систематизацию методов обучения, которые могут эффективно способствовать улучшению уровня математической грамотности. В рамках исследования особое внимание уделялось анализу того, как различные подходы в обучении могут влиять на способность студентов применять математические знания в разнообразных реальных и теоретических контекстах.
Материалы и методы исследования
Экспериментальной базой исследования являлся Кабардино-Балкарский государственный университет им. Х.М. Бербекова (КБГУ). В исследовании приняли участие 68 студентов первых курсов гуманитарных направлений КБГУ, что обеспечило репрезентативность выборки и возможность генерализации полученных результатов. Студентов поделили на две равные группы по 34 чел.: контрольную и экспериментальную. Распределение по группам происходило таким образом, чтобы в каждой группе было примерно одинаковое количество студентов каждого уровня математической подготовки.
Для данного исследования применялся комплекс теоретических и эмпирических методов. В основу теоретического анализа легли методы систематизации и интерпретации научной литературы, что позволило глубже изучить и осмыслить концепцию функциональной математической грамотности. Среди основных теоретических подходов выделялись анализ и обобщение данных, полученных из академических источников, а также критическое осмысление различных методик обучения математике, что способствовало формированию целостного представления о текущем состоянии проблемы.
На эмпирическом уровне был организован педагогический эксперимент с использованием разработанных учебных материалов и заданий, специально адаптированных для формирования и оценки математической грамотности. Применялись такие методы сбора данных, как анкетирование и наблюдение, что позволило оценить динамику усвоения математических навыков студентами. Компьютерное тестирование было использовано для количественной оценки уровня математических знаний и умений студентов, а также для анализа эффективности методик обучения.
Ключевым аспектом практической части исследования стало использование интерактивных досок и мультимедийных презентаций в процессе лекционных и практических занятий. Эти инструменты способствовали визуализации абстрактных математических понятий и улучшению понимания студентами изучаемого материала. Особое внимание уделялось методам активного обучения, включающим решение практических задач, что направлено на стимулирование критического мышления и развитие проблемно-ориентированных навыков у студентов.
Результаты исследования и их обсуждение
На констатирующем этапе в экспериментальной и контрольной группах была проведена входная тестовая диагностика уровня сформированности математической грамотности обучающихся. Результаты входной диагностики оказались примерно сопоставимыми (рис. 1).
Экспериментальная группа проходила интенсивный курс по функциональной математической грамотности, включающий лекции, практические занятия. Контрольная группа продолжала обучение по стандартной программе.
В ходе формирующего этапа, проведенного без изменений в учебных планах, были разработаны и внедрены комплексные методы педагогического анализа, взаимосвязанные и взаимодополняющие друг друга, что позволило достичь поставленных целей в обучении дисциплине «Математика». Реализация экспериментальной части исследования включала использование электронных образовательных технологий и интерактивных досок, что способствовало более глубокому взаимодействию студентов с материалом и улучшению их понимания абстрактных математических концепций через визуализацию.
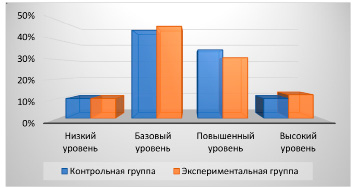
Рис. 1. Результаты входного диагностического тестирования
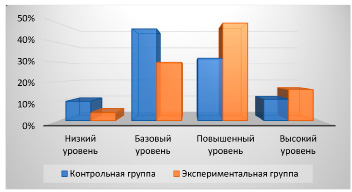
Рис. 2. Результаты итогового тестирования
Для формирования функциональной математической грамотности был создан набор задач, помогающий студентам развивать необходимые навыки и применять теоретические знания на практике. В процессе практических занятий особое внимание уделялось повторению и анализу различных подходов к решению задач, что обеспечивало студентам лучшее освоение материала. Важной частью контрольного этапа стало использование итогового тестирования, позволившего оценить качество усвоения знаний в более структурированной форме, обеспечивая объективность и точность оценок (рис. 2).
Сравнительный анализ результатов входного и итогового тестирования двух групп демонстрирует значительное преимущество интенсивного обучения по специальной программе. Студенты экспериментальной группы показали общий рост уровня математических знаний, при этом значительная часть студентов перешла на более высокие уровни грамотности. В контрольной группе изменений практически не произошло, что подтверждает статичность их уровня знаний без дополнительных усилий по улучшению образовательной программы.
Полученные данные подтвердили, что интеграция традиционных и современных образовательных методов значительно повышает эффективность учебного процесса, способствует более продуктивному взаимодействию студентов с учебным материалом и способствует их активной познавательной деятельности. Это, в свою очередь, позволяет студентам развивать межпредметные и междисциплинарные умения, которые оказываются крайне важными в современных реальных профессиональных контекстах.
Также было выявлено, что дидактические требования к учебным задачам и самостоятельная работа студентов вне аудитории оказывают значительное влияние на развитие творческого мышления и углубленное понимание математических концепций.
В рамках эксперимента было установлено, что интеграция новейших технологий и интерактивных ресурсов в образовательный процесс существенно повышает интерес студентов к учебе. Применение мультимедийных презентаций и интерактивных досок значительно усиливало вовлеченность студентов, способствуя лучшему усвоению материала и пониманию сложных тем.
Исследование показало, что центрирование образовательного процесса вокруг студента и его активного взаимодействия с учебным контентом приводит к улучшению понимания и освоения математических знаний. Этот подход особенно актуален в свете современных образовательных направлений, акцентирующих внимание на развитии навыков, критически важных для профессионального роста и успеха в будущем.
Глубокое осмысление понятия «математическая грамотность» требует всестороннего изучения концепции «функциональной грамотности». На основе данных, полученных в ходе эксперимента в образовательной среде, становится очевидным, что функциональная грамотность служит основой для развития универсальных культурных компетенций, актуальных для студентов разнообразных дисциплин.
Функциональная грамотность определяется как способность человека адекватно осмысливать, анализировать и применять информацию в самых разных жизненных обстоятельствах. В условиях современного мира, полного информационных потоков, такие умения приобретают критическое значение, обеспечивая быструю адаптацию к изменениям и требованиям времени. Ключевым аспектом функциональной грамотности является возможность не только интерпретировать данные, но и осуществлять обдуманный выбор и принимать взвешенные решения, что становится основой для успешного развития личности и профессионального роста.
Заключение
В результате исследования установлено, что необходимо разработать образовательную среду, которая будет способствовать не просто усвоению теоретических знаний студентами, но и развитию их способностей к их практическому применению при анализе и решении конкретных задач. Такой подход позволит студентам не только глубже осознавать математические концепции, но и оценивать их прикладное значение в разнообразных профессиональных областях.



