Введение
Методы линейного программирования (ЛП) нашли применение для широкого класса практических задач в промышленности, торговле, сельском хозяйстве и других областях человеческой деятельности. Использование алгоритмов линейного программирования позволяет планировать производственные ресурсы и мощности, оптимизировать рацион питания животных, планировать размещение сельскохозяйственных культур и позволяет решать целый ряд оптимизационных задач в области микро- и макроэкономики. Математические модели, в том числе модели линейного программирования, дают возможность выбрать наиболее оптимальное управленческое решение из ряда возможных вариантов. Широкому использованию таких моделей на практике способствует и большое число разработанных программных средств решения и анализа задач ЛП.
В зависимости от решаемой задачи математическая запись модели задачи ЛП может несколько отличаться, хотя принципы и математическое обоснование, сформулированные профессором Л.В. Канторовичем [1, с. 32] и американским ученым Дж.Б. Данцигом [2, с. 37], для всех задач данного класса остаются неизменными. В общем случае математическая модель представляет собой линейную относительно неизвестных переменных функцию, для которой требуется определить экстремальное значение на множестве допустимых решений, заданном системой линейных ограничений.
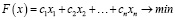
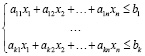. (1)
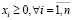
Будем далее называть все неотрицательные решения xi, удовлетворяющие системе линейных ограничений, допустимыми значениями задачи ЛП, а значения переменных xi*, минимизирующих функцию F(x), решением задачи.
Одной из классических задач линейного программирования является задача транспортной логистики, в которой реализуется поиск наиболее оптимального плана перевозок с учетом имеющихся ресурсов и затрат на перевозки. В современных условиях ведения хозяйственной деятельности вопросы, связанные с перевозкой грузов, приобретают важное значение. По оценкам специалистов, в сфере торговли и логистики доля транспортных затрат, связанных с перемещением грузов, может достигать 20–30 %.
Вопросам теоретического и практического исследования транспортной задачи и методов их решения посвящено достаточно много различных статей и монографий. В качестве примера можно привести работы [3–5]. Так, исследователь И.Е. Погодин предлагает способ оценки количества возможных планов решения замкнутых транспортных задач для матриц различной размерности и структуры [3]. С.Н. Медведев рассматривает задачу маршрутизации транспорта с несколькими центрами с чередованием и единым местом сбора [4]. Для решения задачи распределения имеющихся транспортных средств по исходным пунктам с учетом грузоподъемности транспортных средств исследователь Н.М. Нечитайло предлагает использовать метод динамического программирования [5].
Транспортная задача ЛП в качестве решения определяет план оптимальных перевозок и относится к классу двух индексных задач [6, с. 69]. Значения переменных xij определяют объемы перевозимого груза, а индексы соответственно поставщика и потребителя груза. План перевозок такой транспортной задачи удобно представить матрицей X, имеющей размерность k×n, где k – число поставщиков и n – число заказчиков груза:
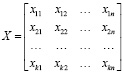. (2)
Для каждой доставки, заданной парой индексов i,j, затраты на перевозку единицы груза определяются параметрами sij. Матрица затрат на перевозку S, как и матрица переменных X, имеет размерность k×n:
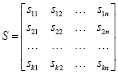. (3)
Минимизация затрат на перевозку может быть представлена оптимизационной математической моделью. С учетом введенных обозначений и имеющихся ограничений модель задачи имеет вид
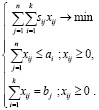(4)
Ограничения ai определяют запасы поставщиков, ограничения bj – заказы потребителей.
В классической транспортной задаче все параметры считаются детерминированными. В то же время, если параметры, определяющие запасы поставщиков ai, а также параметры, определяющие заказы потребителей bj, чаще всего точно определены, то затраты на перевозку могут зависеть от целого ряда случайных факторов. В данной статье рассматривается ситуация, когда матрица затрат на перевозку единицы груза представляет собой набор случайных величин с распределением плотности вероятности, близкой к нормальному закону.
Цель исследования – разработку математических методов и алгоритмов учета неопределенностей исходных параметров при решении задач ЛП.
Материалы и методы исследования
Для подготовки статьи использованы материалы научных исследований, опубликованные в статьях и монографиях отечественных и зарубежных специалистов, а также электронные ресурсы интернета, находящиеся в открытом доступе.
Методы проведения исследований основаны на использовании методов линейной алгебры, математической статистики и линейного программирования, алгоритмов решения оптимизационных задач. В работе использованы методы численного моделирования для проверки работоспособности предлагаемых решений. Моделирование тестовых задач выполнено с использованием программных пакетов оптимизации Pythonи пакета визуализации Matplotlib.
Результаты исследования и их обсуждение
Будем считать затраты на перевозку единицы груза от поставщика потребителю случайными величинами. Параметры распределения случайных величин зададим матрицей математических ожиданий Q и матрицей ковариаций C (5). Обозначим через p общее число маршрутов. С учетом ранее введенных обозначений p = n×k.
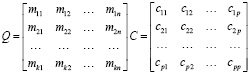. (5)
Общие затраты на перевозку в данной постановке задачи – случайная величина, характеризующаяся математическим ожиданием M и вариацией V. Математическое ожидание может быть рассчитано как сумма произведений объемов перевозимого груза и математических ожиданий стоимости перевозки единицы груза. С учетом введенных обозначений (2) и (5) значение M будет равно
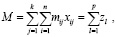(6)
где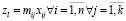 
.
Вариация V определяет численное значение риска. Источниками вариации могут быть самые различные факторы, возникающие в процессе перевозок по маршрутам следования. Такими факторами могут быть неблагоприятные погодные условия, транспортная загруженность маршрута следования, состояние дорожного полотна, особенности перевозимого груза и ряд других факторов.
Значение вариации V определяется выражением
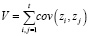. (7)
Число слагаемых tв последнем выражении определяется как число сочетаний
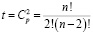. (8)
В случае отсутствия взаимной корреляции отдельных доставок значение V будет равно сумме дисперсий случайных величин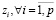 
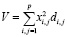(9):
. (9)
На основании приведенных выше соотношений транспортная задача может рассматриваться как двухкритериальная оптимизационная задача минимизации стоимости перевозок и минимизации рисков. В данном случае под риском понимается отклонение суммарных затрат на доставку от ранее планируемых. Численные значения вариаций определяются на основании данных временных рядов предыдущих периодов и могут постоянно уточняться на основании новых наблюдений. При этом не исключено наличие временного тренда и периодической составляющей.
Наличие многокритериальной неопределенности не позволяет выбрать решение, минимизирующее оба критерия в области допустимых решений, заданной системой линейных неравенств. Для выбора эффективного, по Парето, решения для двухкритериальной задачи можно использовать различные компромиссные подходы, ряд которых описан в работах [7, с. 67; 8].
В данной работе предлагается использование алгоритма решения, основанного на выборе основного критерия многокритериальной оптимизационной задачи. В качестве такого критерия выбраны риски перевозок, тогда как затраты на перевозку в этом случае должны быть заданы в виде дополнительного ограничения. В качестве такого ограничения может быть задано некоторое допустимое значение M0. Математическая модель задачи определяется следующими выражениями:
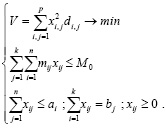(10)
С учетом нелинейной зависимости функции V(x) данная задача может быть отнесена к классу нелинейного программирования, а как частный случай – к задачам квадратичного программирования. Для задач указанного класса могут быть использованы алгоритмы численных методов поиска оптимальных значений.
В зависимости от исходных данных задачи для решения могут быть использованы надстройка Excel «Поиск решения», пакеты оптимизации pulp, scipy.optimize, cvxopt.modeling в среде Python и ряд других распространенных инструментов оптимизации.
В качестве практического примера и решения транспортной задачи с использованием предлагаемого в данной работе подхода рассмотрим задачу по доставке однородных грузов от трех поставщиков пяти потребителям. Себестоимости доставок заданы математическими ожиданиями в табл. 1, вариации по отдельным доставкам приведены в табл. 2.
Поскольку имеющиеся в пунктах отправления запасы превышают общий объем заказов, задача относится к классу открытых транспортных задач.
Решения приведенной оптимизационной задачи для всего возможного диапазона значений представлены на рис. 1.
В зависимости от выбранного значения на кривой Парето решения будут иметь разные значения. Так, матрица решений для M0 = 900 представлена в табл. 3.
Таблица 1
Себестоимость перевозки единицы груза
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
7 |
6 |
8 |
10 |
12 |
60 |
|
А2 |
9 |
5 |
7 |
4 |
6 |
60 |
|
А3 |
6 |
8 |
4 |
9 |
7 |
50 |
|
Заказы |
30 |
20 |
55 |
20 |
25 |
Таблица 2
Матрица вариаций
|
В1 |
В2 |
В3 |
В4 |
В5 |
|
|
А1 |
0,5 |
0,8 |
0,5 |
0,7 |
0,6 |
|
А2 |
0,1 |
1 |
0,8 |
1,2 |
1 |
|
А3 |
0,6 |
1,2 |
0,8 |
1,1 |
0,9 |
Таблица 3
Решения по объемам перевозимых грузов
|
В1 |
В2 |
В3 |
В4 |
В5 |
|
|
А1 |
14 |
10 |
17 |
1 |
0 |
|
А2 |
3 |
10 |
14 |
17 |
14 |
|
А3 |
13 |
0 |
24 |
2 |
11 |
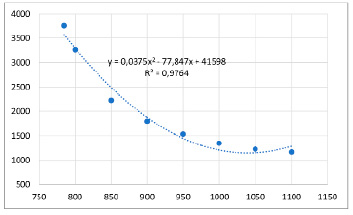
Рис. 1. Зависимость затрат на перевозку грузов и рисков
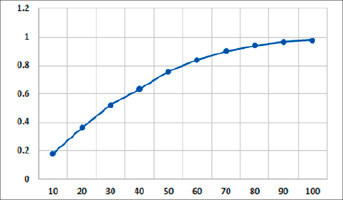
Рис. 2. Зависимость значений вероятности отклонения от его величины
Используя функцию Лапласа, найдем зависимость вероятности отклонения величины затрат на перевозку от заданного значения М0. Воспользуемся функцией Лапласа для нормального распределения случайной величины:
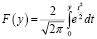. (11)
Значение вероятности при этом вычисляется в соответствии со следующим выражением для табличной функции Лапласа:
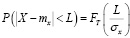. (12)
Для заданного в рассматриваемом примере значения M0 = 900 значение вариации составляет 1800, а среднеквадратическое отклонение соответственно 42,4. График зависимости вероятности от значения отклонения случайной величины приведен на рис. 2.
Данный пример демонстрирует методику определения эффективного, по Парето, решения транспортной задачи в условиях неопределенности исходных данных, задающих затраты на перевозку.
Заключение
Вопрос оптимизации перевозок всегда остается актуальным, поскольку затрагивает важнейшие стороны человеческой деятельности, такие как производство, торговля, военная отрасль и ряд других важных направлений. Задачи планирования перевозок имеют широко используемую математическую модель, подкрепленную множеством разработанных методов и программ для ее решения. В то же время представляет интерес практическая ситуация, когда исходные параметры задачи не могут быть точно определены. В данной статье предлагается модель транспортной задачи, учитывающая неопределенность исходных данных. Предлагаемый подход, основанный на статистических оценках неопределенности, позволяет оценить как затраты на перевозку грузов, так и вероятность отклонения затрат от плановых значений. Предложенная модель, а также алгоритм решения могут быть использованы в логистических расчетах планирования перевозок. Практическое применение предлагаемого подхода наиболее актуально и может быть рекомендовано в условиях крупных населенных пунктов при организации регулярных перевозок грузов.