Введение
Развитие наукоемких производств и инновационных технологий приводит к необходимости постоянного усовершенствования технологических процессов внедрения новейших разработок, позволяющих в целом повысить конкурентоспособность и востребованность продукции предприятий, в том числе в области текстильной промышленности [1]. Так, развивается создание наномодифицированных текстильных материалов различного назначения, что, в свою очередь, приводит к необходимости к постоянному поиску, разработке и внедрению все новых методов, позволяющих выявлять наночастицы с высокой точностью [2, 3].
Для обеспечения высокой разрешающей способности (до 10-16) при идентификации наночастиц металлов применяются методы рамановской спектроскопии с разработкой и внедрением различных способов усиления сигнала [4]. Одним из эффективных методов повышения разрешающей способности является использование корреляционных многомерных взаимозависимостей, а также гипотезы Байеса [5]. Однако следует учитывать, что математическая обработка большого количества исследуемых параметров крайне затрудняет определение взаимозависимых вероятностей и приводит к необходимости преобразования корреляционных параметров в некоррелированный вид. При этом получены математические решения вышеупомянутой задачи в работах [6, 7], однако их недостатком является то, что в них многомерные системы уравнений решаются отдельно для плотностей вероятностей и отдельно для эквивалентных радиусов эллипсов распределений рамановских спектров. Это приводит к необходимости проводить анализ полученных результатов и выбирать исходя из этого оптимальный вариант с учетом лучшей достоверности для оценки наличия наночастиц. Поэтому актуальной является задача разработки математического инструментария для идентификации наночастиц, который позволит одновременно учитывать и плотности вероятностей, и эквивалентные радиусы.
Цель исследования – поиск оптимального решения задачи повышения точности определения наночастиц серебра на текстильных волокнах на основе многомерного аналитического анализа.
Материалы и методы исследования
В качестве основного материала использовались наномодифицированные полиэфирные волокна, обработанные 17 %-ным раствором коллоидного серебра. В работе применялись методы многомерного математического анализа для обработки данных рамановских спектров исследуемых материалов и технология компьютерного моделирования в программе Mathcad.
Для достижения поставленной цели проводимого исследования необходимо выполнить аналитическое преобразование многомерных систем уравнений с учетом перевода данных в независимый вид. Разработана аналитическая форма уравнений вероятности пересечения эллипсов интенсивностей одного пика рамановского спектра волокон с наночастицами и без наночастиц серебра:
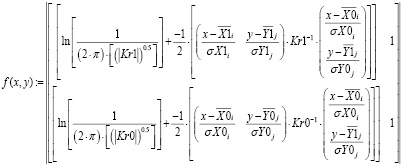 , (1)
, (1)
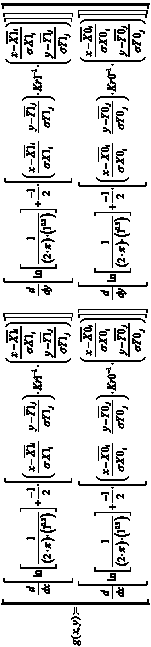 . (2)
. (2)
В рамках данного исследования предложена методика преобразования данных в некоррелированный вид с использованием матриц Krp0 и Krp1 [7]. В результате была получена система уравнений (3), (4) в векторно-матричной форме:
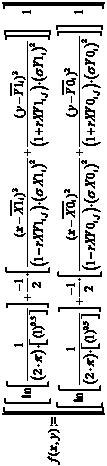 , (3)
, (3)
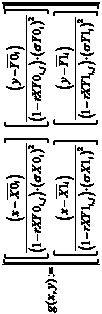 . (4)
. (4)
Преобразование уравнений (3), (4) в аналитическую форму позволяет получить систему аналитических уравнений (5), (6):
 , (5)
, (5)
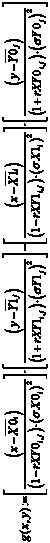 . (6)
. (6)
Результаты исследования и их обсуждение
На основании системы аналитических уравнений (5) и (6) в математической программе Mathcad в работе было получено их решение относительно p1 и p0:
i: = 3 j: = 4
Given
f(x,y) = 0 g(x,y) = 0
v2: = Find(x,y)

f(v20, v21) = 2.8421709430404007×10-14
g(v20, v21) = 3.2526065174565133×10-19
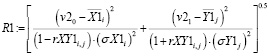 , (7)
, (7)
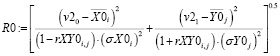 , (8)
, (8)
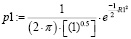 ;
; 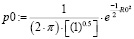 , (9)
, (9)
p1 = 5.040679571258114×10-28 p0 = 5.040679571258114×10-28 (10)
R1: = 20.5∙(-ln(p1) – ln(2∙π))0.5 (11)
R0: = 20.5∙(-ln(p0) – ln(2∙ π))0.5 (12)
При оценке R1 и R0 по аналитическому выражению (7) и (8) получаем
R0 = 11.046896815745413 и
R1 = 11.046896815745413
очень близкие значения.
По аналитическому выражению (9) получаем для
p0 = 5.040679571258114 ∙10-28,
p1 = 5.040679571258114 ∙10-28
практически одинаковые значения.
С использованием аналитических выражений (11) и (12) были определены
R0 = 11.046896815745413,
R1 = 11.046896815745413
такие же и равные по значению.
Отсюда можно сделать вывод: взаимное применение выражений р1 (9) и R1 (11), а также R0 (1), p0 (9), p1 (10) и R0 (12) дает возможность их использовать для взаимного перерасчета p0↔R0 и p1↔R1.
Соответственно, можно констатировать, что уравнения (1)–(6) составлены без ошибок, а решение их проверено и показало высокую достоверность по (10)
p0 = 5.040679571258114 ∙10-28,
p1 = 5.040679571258114 ∙10-28.
Проверка по (11) и (12) показала также высокую достоверность составления и решения системы уравнений (1)–(12).
Для проверки и подтверждения составления и решения системы уравнений (1)–(12) построено графическое изображение пересечения эллипсов рамановских спектров в точке
v20 = 573.769592 и v21 = 3296.83997,
которое представлено на рис. 1.
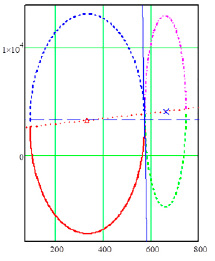
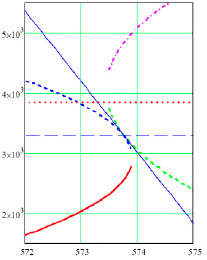
а) б)
Рис. 1. Эллипсы распределения рамановских спектров полиэфирных волокон с наночастицами серебра и без наночастиц с преобразованием двумерных параметров в независимый вид: а) общий вид пересечения; б) увеличенный фрагмент
При этом изображение выполнено при привязке распределения данных к оси MENY0j – – MENY1j для
p0 = 5.040679571258114 ∙10-28,
p1 = 5.040679571258114 ∙10-28,
R0 = 11.046896815745413,
R1 = 11.046896815745413.
Аналитическое и графическое решение системы дифференциальных уравнений показало высокую достоверность:
p0 = 5.040679571258114 ∙10-28 и
p1 = 5.040679571258114 ∙10-28.
И следует подчеркнуть, что нет необходимости составлять и решать систему уравнений для преобразованных не корреляционных уравнений отдельно для R0, R1 и отдельно для p0, p1. Решение возможно по R0, R1 для p0, p1 с перерасчетом по аналитическим выражениям (11) и (12). Это значительно упрощает сложные составления и решения систем дифференциальных нелинейных корреляционных уравнений. Это видно по уравнениям (5) и (6), где нет члена ln[1/2π∙(1)0.5], когда уравнение (3) превращается в уравнение (5).
Для проверки точности вычисленных значений R0 и R1 при составлении и решении системы некорреляционных уравнений по p0 и p1 покажем матрицу значений p0 и p1 для десятизначных обратных значений (13) и матрицу столбцов с максимальными десятизначными после запятой значениями строк R0 и p0. Это необходимо для более удобной формы оценки эффекта от преобразования системы уравнений в некорреляционный вид (1)–(12), при этом используем термин достоверность вместо плотностей вероятностей:
QL00=log(1/р0). (13)
Так как использовать приходится степенные выражения с очень большими значениями для достоверности и плотностей вероятностей, то удобнее применять их логарифмические значения с использованием выражения (13).
Эквивалентные радиусы эллипсов распределений рамановских спектров волокон с наночастицами серебра и без наночастиц, полученные в ходе проведения исследования, приведены на рис. 2 для удобства в раздельных матрицах столбцов R01–R09 из-за очень большого объема 17-разрядных десятичных значений в каждом члене матрицы столбца.

Рис. 2. Значения эквивалентных радиусов для девяти пиков рамановского спектра
Так как здесь приведены радиусы эллипсов распределения только для данных пиков рамановского спектра для диэлектрика волокон без наночастиц R0 при решении систем уравнений, а для волокон с наночастицами значения радиусов R1 практически равны R1~ R0, то в этом исследовании нет пока необходимости приводить значения матриц R1.
В дальнейших исследованиях точностей решения системы уравнений (1)–(12) будет необходимость использовать совместно и R0 и R1.
Вычисление значений p01–p09, представленных на рис. 3, проводилось по выражениям (9)–(10).
По рис. 3 видно, что приведены только значения p0 для девяти пиков рамановского спектра волокон без наночастиц p0. Поскольку для волокон с наночастицами значения плотности вероятностей p1 практически равны p1~ p0, то в этом исследовании нет пока необходимости приводить значения матриц p1.
В дальнейших исследованиях точностей решения системы уравнений (1)–(12) будет необходимость использовать совместно и p0 и p1.
Матрица, представленная выражением (16), приведена здесь с уменьшенным количеством десятичных разрядов в каждом 81 члене из-за удобства представления достоверности. Вычисления были осуществлены с использованием компьютерных технологий в программе Mathcad по 16 разрядов после запятой с максимальным разрешением.
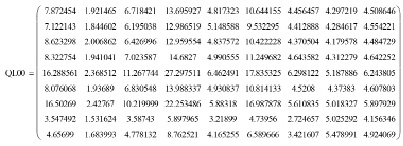 (16)
(16)

Рис. 3. Значения плотностей вероятности для девяти пиков рамановского спектра
При умножении независимых вероятностей P0 = ∏Pi с использованием их логарифмических выражений (13) были получены суммы логарифмов достоверностей SQL00 (17) из (16)
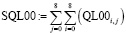 , SQL00 = 564.1545106983666. (17)
, SQL00 = 564.1545106983666. (17)
А для одного пика в среднем получены следующие результаты:
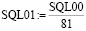 , SQL01 = 6.964870502448971. (18)
, SQL01 = 6.964870502448971. (18)
При этом плотности вероятностей будут иметь следующие значения:
для общей системы p00 = 10-564.1545106983666, (19)
для одного пика рамановского спектра средняя плотность вероятностей составляет
p001 = 10-6.964870502448971. (20)
Если рассмотреть составление и решение системы уравнений при привязке данных к оси MENY0j = 0 – – MENY1j = 0 по сравнению с системой уравнений с привязкой данных к оси MENY0j – – MENY1j (19) и (20), то получим матрицу достоверностей QL00φ (21):
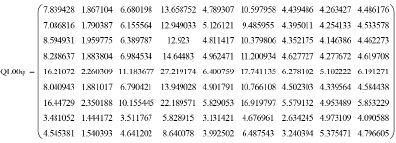 (21)
(21)
На следующем этапе выполнения исследования при умножении независимых вероятностей P0 = ∏Pi при использовании их логарифмических выражений (13) получены суммы логарифмов достоверностей SQL00φ (22) из (21):
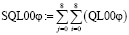 , SQL00φ = 559.5602718672014. (22)
, SQL00φ = 559.5602718672014. (22)
А для одного пика в среднем получены результаты:
SQL01φ = SQL00φ/81, SQL01φ = 6.908151504533351. (23)
При этом плотности вероятностей будут иметь следующие значения:
для общей системы – p0φ = 10-559.5602718672014, (24)
для одного пика рамановского спектра средняя плотность вероятностей составляет
p01φ = 10-6.90815150453335. (25)
Таким образом, при составлении и решении системы уравнений при привязке данных к оси MENY0j – – MENY1j достоверность SQL00 дает более высокое значение, чем SQL00φ, полученная при привязке данных к оси MENY0j = 0 – – MENY1j.
Заключение
В работе предложен метод аналитического представления преобразованной системы корреляционных уравнений плотностей вероятностей в некорреляционные уравнения эквивалентных радиусов эллипсов разброса рамановских спектров полиэфирных материалов как с наночастицами серебра, так и без них.
При решении по аналитическому выражению системы уравнений эквивалентных радиусов получены очень близкие значения максимального пика
R0 = 11.046896815745413 и
R1 = 11.046896815745413.
По аналитическому выражению для системы уравнений плотностей вероятностей получены
p0 = 5.040679571258114 ∙10-28,
p1 = 5.040679571258114 ∙10-28
практически также одинаковые значения.
С использованием аналитических выражений
R0 = f(p0) и R1 = f(p1)
вычислены такие же и равные значения
R0 = 11.046896815745413,
R1 = 11.046896815745413.
Таким образом, обеспечивается сходимость баз уравнений p0 и p1, R0 и R1 в 15-м десятичном знаке.
Отсюда следует, что взаимное применение выражений р1 и R1, а также R0, p0 дает возможность их использовать для взаимного перерасчета p0↔R0 и p1↔R1. Это позволяет для оценки наличия наночастиц использовать только систему для эквивалентных радиусов.
Соответственно, можно сделать вывод, что уравнения системы составлены без ошибок, а решение их проверено и показало высокую достоверность по
p0 = 5.040679571258114 ∙10-28,
p1 = 5.040679571258114 ∙10-28.
Для проверки и подтверждения достоверности составления и решения системы уравнений построено графическое изображение пересечения эллипсов рамановских спектров в точке
v20 = 573.769592 и v21 = 3296.83997
решения системы уравнений.
Получена при умножении независимых вероятностей P0 = ∏Pi с использованием их логарифмических выражений сумма логарифмов достоверностей
SQL00 = 564.1545106983666,
а для одного пика в среднем получено значение
SQL01 = 6.964870502448971.
При таких значениях логарифмических выражений плотности вероятностей будут иметь следующие значения:
для общей системы p00 = 10-564.1545106983666,
а для одного пика рамановского спектра средняя плотность вероятностей следующая:
p001 = 10-6.964870502448971.
Дополнительно рассмотрено составление и решение системы уравнений при различных привязках данных к осям. В результате было установлено, что при привязке данных к оси MENY0j – – MENY1j достоверность SQL00 по сравнению с системой уравнений с привязкой данных к оси MENY0j = 0 – – MENY1j = 0 с достоверностью SQL00φ дает более высокое значение достоверности SQL00, чем значение SQL00φ.
На основании полученных результатов для идентификации наночастиц различных концентраций коллоидного серебра возникает необходимость в дополнительном проведении исследований для повышения достоверности и эффективности распознавания наночастиц золота на диэлектрических и полупроводниковых волокнах.



