Введение
Для оценки оптимальных условий прохождения сигналов в информационных каналах различного назначении важен прогноз степени воздействия возмущающих факторов канала на характеристики сигнала [1–3]. В то же время измерения вариаций характеристик сигнала, вызванных возмущениями канала, можно использовать для контроля и идентификации возмущающих факторов. Среди множества измеряемых характеристик принятого сигнала его групповая задержка содержит важную интегральную информацию о состоянии канала. Поэтому представляет значительный практический интерес разработка оперативных методов и алгоритмов расчета групповой задержки сигнала в каналах, наиболее приближенных к реальным. Для оценки групповой задержки сигнала в ряде случаев используется упрощенная модель канала с бесконечной кривизной, однако такая модель не всегда соответствует геометрии задачи. В работе [4] была предложена численная схема расчета направления распространения и рефракционного ослабления потока энергии сигнала в возмущенном информационном канале с конечной кривизной. В настоящей работе эта схема развита и использована для расчета групповых задержек сигналов в каналах просвечивания космической среды.
Цель исследования заключается в создании оперативной численной схемы расчета групповой задержки сигнала в возмущенном диэлектрическом канале с конечной кривизной.
Основные математические соотношения
Для расчета групповой задержки сигнала при распространении в канале с регулярными возмущениями диэлектрической проницаемости в качестве опорного математического аппарата использовались нелинейные дифференциальные уравнения геометрической оптики в форме Эйлера, полученные из принципа Ферма [5, с. 21]. С учетом конечной кривизны канала в полярной системе координат имеем:
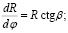
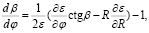 (1)
(1)
где R(φ), φ – радиальная и угловая координаты луча; β(φ) – угол рефракции луча, ε – диэлектрическая проницаемость канала. В приближении геометрической оптики групповая задержка сигнала определяется как интеграл по траектории:
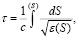 (2)
(2)
где c – скорость света; dS – элемент дуги.
Непосредственный численный расчет интеграла (2) с использованием широко известных квадратурных формул Ньютона–Котеса, Гаусса и иных [6, с. 86] требует значительных временных затрат, поскольку для пошагового вычисления подынтегральной функции ε(S) в (2) необходимо многократное численное интегрирование системы уравнений (1). Однако сведение интеграла (2) к дифференциальному уравнению первого порядка позволяет сделать численную схему расчета групповой задержки более оперативной. Дифференцируя (2) по переменному верхнему пределу, имеем:
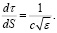 (3)
(3)
Представляя элемент дуги dS в полярной системе координат, уравнение для групповой задержки сигнала запишем в виде:
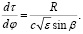 (4)
(4)
Объединяя формулы (1) и (4), имеем систему дифференциальных уравнений для одновременного расчета траекторных характеристик и групповой задержки сигнала в канале с конечной кривизной:
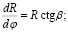
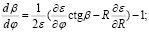
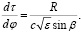 (5)
(5)
Следует заметить, что временные затраты, необходимые для вычисления групповой задержки сигнала с помощью системы (5), значительно меньше, чем в случае непосредственного вычисления (2), когда требуется предварительный расчет системы уравнений (1) на каждом шаге интегрирования. Выигрыш во времени расчета τ с использованием численной схемы на основе (5) составляет ≈mΔt, где Δt – время расчета системы (1) для определения подынтегральной функции на одном шаге при непосредственном численном расчете интеграла (2); m – количество шагов.
Моделирование групповой задержки сигнала в канале с регулярными возмущениями диэлектрической проницаемости проводилось на основе системы (5) для краевых задач Коши и Дирихле. Численные расчеты (5) выполнялись с использованием функции odeint (библиотека scipy) на языке программирования Python. В основу функции положен классический численный метод интегрирования систем обыкновенных дифференциальных уравнений Рунге–Кутта 4-го порядка.
Тестирование алгоритма расчета
Для правильной физической интерпретации результатов моделирования групповой задержки сигналов в каналах различного назначения требуется тестирование предложенной вычислительной схемы. С этой целью было получено аналитическое решение системы (5) для простой слоистой модели диэлектрической проницаемости канала. Переходя в (5) от независимой переменной φ к переменной R, для расчета групповой задержки имеем:
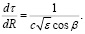 (6)
(6)
При замене в (6) переменной
R = REarth + z,
где REarth – радиус кривизны канала, и выполняя предельный переход REarth → ∞, уравнение (6) преобразуется к виду:
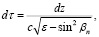 (7)
(7)
где βn – начальный угол излучения, и учтен закон Снеллиуса [5, с. 126]:
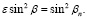 (8)
(8)
В качестве модели диэлектрической проницаемости канала используем зависимость:
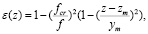 (9)
(9)
где fcr – критическая частота; zm – высота минимума диэлектрической проницаемости; ym = zm – zn – полутолщина канала; zn – координата входа сигнала в канал. Интегрируя уравнение (7) с учетом (9), для групповой задержки сигнала получаем:
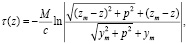 (10)
(10)
где
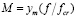 ;
;
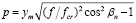 .
.
Решение (10) было использовано для проверки предложенной численной схемы расчета на основе системы (5).
Задавались следующие начальные условия: R(φ = 0) = Rn = REarth; β(φ = 0) = βn, значения прицельного углового параметра βn находились в секторе [0.15;1.05]rad, высота минимума диэлектрической проницаемости Rm = (REarth + 350) км, критическая частота fcr = 9 МГц. Результаты моделирования групповой задержки сигнала при двух значениях прицельного параметра βn представлены на рисунке 1.
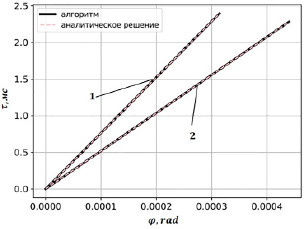
Рис. 1. Сравнение численных и аналитических расчетов групповой задержки сигнала τ(φ) при различных значениях прицельного параметра βn: 0.314rad (1) и 0.473rad (2)
Нетрудно заметить высокую точность совпадения численных и аналитических расчетов. Порядок расхождения кривых составил в среднем 2 мкс. Такие малые отличия позволяют заключить, что предложенная численная схема расчета достаточно надежна и может быть использована для оценки групповой задержки сигналов в каналах с конечной кривизной.
Численные эксперименты
Для демонстрации численной схемы расчета групповой задержки сигнала в возмущенном канале были поставлены численные эксперименты. Рассматривались каналы просвечивания земной и солнечной атмосферы.
Модель диэлектрической проницаемости верхней атмосферы (ионосферы) в присутствии волнового возмущения задана в виде:
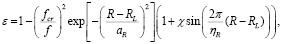 (11)
(11)
где RL – радиальная координата максимума ионосферной ионизации; aR – полутолщина ионосферного слоя; χ, ηR – интенсивность и длина волны возмущения соответственно. Расчеты на основе системы (5) с краевыми условиями Дирихле позволяют оперативно оценить степень воздействия волнового возмущения на состояние трансионосферного канала в режиме многочастотной передачи с космического аппарата.
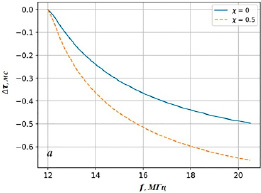
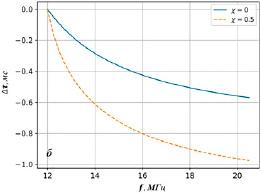
Рис. 2. Относительные групповые задержки сигналов на различных частотах: a – φk = 0.031 rad; б – φk = 0.053 rad f [12;20] МГц; fcr = 9 МГц; RL = 6721 км; aR = 290 км; ηR = 50 км
В качестве примера на рисунке 2 приведены рассчитанные зависимости разностей групповых задержек сигналов на различных рабочих частотах и групповой задержки сигнала на опорной частоте для двух разнесенных приемников, расположенных на Земле.
Далее рассматривался канал просвечивания околосолнечной плазмы радиоизлучением залимбового коронального источника в присутствии коронального выброса массы (КВМ) [4, 7]. Задавалась модель диэлектрической проницаемости возмущенного околосолнечного канала в виде:
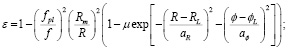 (12)
(12)
где fpl – плазменная частота на некотором расстоянии Rm = 5Rs от центра Солнца; Rs – радиус Солнца; μ – безразмерный параметр полости КВМ; RL, φL – радиальная и угловая координаты центра КВМ; aR, aφ – радиальный и угловой масштабы коронального возмущения соответственно. На рисунке 3 представлены рассчитанные на основе (5) относительные групповые задержки сигналов на различных рабочих частотах для двух разнесенных приемников, расположенных на орбите Земли.
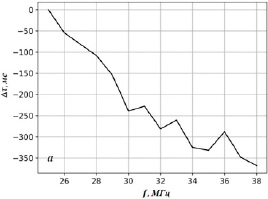
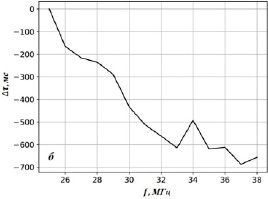
Рис. 3. Частотно-временные характеристики радиовсплесков при различных положениях приемной антенны: a – φk = 2.74 rad; б – φk = 2.84 rad f [25;39] МГц; fpl = 19 МГц; μ = 1.7; RL = 5 Rs; φL = 0.4 rad; aR = 0.15 Rs; aφ = 0.63 rad
В частности, из рисунка 3б следует, что при расположении источника коронального радиовсплеска в более глубокой залимбовой области разность групповых задержек между соседними частотами значительно возрастает. Этот рост вызван увеличением времени распространения сигнала через полость КВМ вследствие волноводного механизма распространения [4]. Следует заметить, что для диагностики параметров КВМ по измеренным групповым задержкам принятых радиовсплесков частотный диапазон излучения [25;33] МГц является важным, поскольку на частотах, больших 33 МГц, относительные групповые задержки стремятся к постоянному значению и становятся неинформативными.
Универсальность предложенной численной схемы расчета групповой задержки сигнала позволяет решать и более сложные задачи. В частности, был поставлен численный эксперимент для оценки задержки сигнала в гравитационном поле массивного объекта с учетом окружающей его плазмы. Одним из следствий общей теории относительности (ОТО) является замедление времени распространения электромагнитного сигнала под воздействием поля тяготения астрофизического объекта (эффект Шапиро) [8, с. 172]. Окружающая плазма также влияет на процесс распространения, в особенности на сигналы радиодиапазона. Более высокочастотные диапазоны электромагнитной шкалы в меньшей степени подвержены влиянию плазмы, что приводит к более явному проявлению эффектов гравитационного линзирования. В качестве примера рассматривалась задача распространения электромагнитного излучения вблизи Солнца. Для оценки групповой задержки сигнала в околосолнечной среде использовалась модель диэлектрической проницаемости в виде:
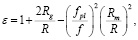 (13)
(13)
где Rg – гравитационный радиус Солнца (Rg ≈ 3 км). Источник излучения и приемная антенна находились на земной орбите с радиусом 1 а.е. (≈1.5∙108 км). Параметры невозмущенной околосолнечной плазмы были взяты те же самые, что и в предыдущем численном эксперименте. На рисунке 4 представлены рассчитанные на основе (5) дистанционно-временные характеристики сигналов просвечивания Солнца на различных рабочих частотах. По оси абсцисс отложены конечные значения угловых координат лучей, пришедших на земную орбиту, а по оси ординат – разности групповых задержек сигналов в среде (13) и в вакууме (ε = 1). Расчеты выполнены с учетом краевых условий Дирихле.
Из рисунка 4 следует, что кривая 3, рассчитанная для высокочастотного сигнала, отображает главным образом эффект гравитационного воздействия Солнца в широком диапазоне координат приемника на орбите Земли. Однако влияние плазмы в этом случае слабо выражено вследствие ее прозрачности.
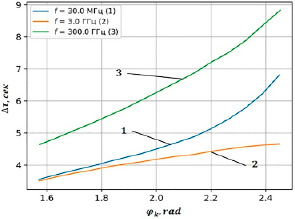
Рис. 4. Дистанционно-временные характеристики сигналов просвечивания Солнца на различных рабочих частотах: Rg = 3 км; βn [–0.76;–0.32]rad; fpl = 15 МГц; Rm = 5 Rs
Кривая 1 соответствует процессу распространения низкочастотного сигнала, когда эффекты плазмы становятся определяющими по сравнению с воздействием поля тяготения Солнца. В поведении кривой 2 прослеживается эффект частичной компенсации воздействия плазмы и гравитационного поля на распространение электромагнитного сигнала промежуточных рабочих частот. Таким образом, численное моделирование на основе (5) позволяет оценить частотный диапазон электромагнитных волн, когда при интерпретации результатов измерений групповой задержки сигнала, связанной с воздействием поля тяготения астрофизического объекта, можно пренебречь эффектами влияния окружающей плазмы.
Заключение
Предложена оперативная численная схема расчета групповой задержки сигнала в диэлектрическом канале конечной кривизны. Интеграл по траектории для групповой задержки сигнала вычисляется совместно с опорной системой дифференциальных уравнений в форме Эйлера, полученных из принципа Ферма. Численное интегрирование расширенной системы уравнений с краевыми условиями Коши и Дирихле выполняется с применением функции odeint (библиотека scipy) на языке программирования Python. Проведено тестирование численной схемы расчета групповой задержки сигнала. Приведены примеры моделирования групповых задержек сигналов в возмущенных каналах просвечивания земной и солнечной атмосферы.



