Введение
На большинстве промышленных предприятий наблюдается значительный рост доли частотно-регулируемого электропривода, внедрение которого позволяет существенно улучшить качество производственных операций и увеличить производительность. При этом большая часть управляемого электропривода на данный момент строится на базе асинхронных электроприводов, которые обладают высокой степенью надежности, относительно невысокой ценой, и при этом их техническое обслуживание достаточно простое [1].
В зависимости от объекта управления и требуемых задач используют различные системы управления электроприводом, которые можно выделить в две группы: скалярное управление и векторное управление.
Скалярное управление основано на математическом аппарате, позволяющем управлять выходным напряжением и его частотой, поддерживая их в заданном отношении. Скалярное управление чаще всего применяют для электроприводов, работающих в условиях, где переменная нагрузка минимальна, отсутствуют жесткие требования к диапазону регулирования и не требуется высокая динамика (насосы, вентиляторы, компрессоры, при этом допускается возможность их группового подключения). Скалярные системы управления могут быть реализованы как разомкнутыми, без каких-либо дополнительных датчиков, так и замкнутыми, по скорости или по какой-либо другой выходной величине, например по величине выходного давления в магистрали, в системах стабилизации напора [2].
Векторное управление, в отличие от скалярного, позволяет контролировать не только величину и частоту выходного напряжения частотного преобразователя, но и его фазу, то есть контролируются величина и угол пространственного вектора напряжения. Векторное управление позволяет производить регулирование скорости с высокой точностью даже в условиях постоянно изменяющейся нагрузки и высокими значениями пускового момента (грузоподъемные механизмы, станки для металлообработки, лифты, экструдеры, дробилки, конвейеры). В связи с тем, что в основе алгоритма векторного управления лежит принцип преобразования координат, а именно переход от трехфазной неподвижной системы координат к двухфазной подвижной, для осуществления этого преобразования необходима информация о положении ротора. Получить эту информацию можно напрямую от двигателя, при помощи установки датчика положения, либо организацией бездатчиковой системы управления, путем введения в систему управления специализированного блока, наблюдателя [3].
Цель исследования – разработка имитационной модели наблюдателя состояний для систем векторного управления асинхронными электроприводами, которая по измеренным току и напряжению позволяет узнать потокосцепление ротора, скорость вращения ротора и электромагнитный момент, позволяет изучать и разрабатывать замкнутые бездатчиковые системы скалярного и векторного управления
Описание блока наблюдателя
Блок наблюдателя позволяет в режиме реального времени получить информацию о положении ротора, скорости вращения двигателя и потокосцеплении, используя для расчета параметры двигателя и данные о фазных напряжениях и токах двигателя. В некоторых случаях блок наблюдателя применяют и для построения бездатчиковых замкнутых систем скалярного регулирования, ведь исключения физического датчика скорости из системы управления позволяют уменьшить итоговую стоимость электропривода, а также повысить его эксплуатационные показатели и упростить процесс наладки [4].
В общем случае наблюдатель состояния представляет собой модель, подключаемую параллельно к объекту управления и получающую информацию об изменениях регулируемой величины посредством отслеживания регулирующих величин. Можно выделить три группы наблюдателей [5]:
1) измеряющие (непрямые измерители положения и измерители ошибки ориентирования);
2) на основе математических моделей (неадаптивные и адаптивные);
3) наблюдатели на основе фильтра Калмана.
На практике чаще всего встречается именно вторая категория наблюдателей, построенная на базе упрощенных математических моделей двигателя. Главным преимуществом данной категории наблюдателей является относительная простота используемого математического аппарата, при достаточно высокой точности.
В первую очередь ко входным величинам тока и напряжения применяется преобразование Кларк, позволяющее перейти от трехфазной неподвижной системы координат к двухфазной неподвижной системе координат.
1. Преобразование Кларк для фазных токов имеет вид
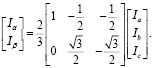 (1)
(1)
2. Преобразование Кларк для фазных напряжений имеет вид
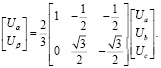 (2)
(2)
3. Преобразование Кларк для линейных напряжений можно вывести из преобразования Кларк для фазных напряжений:
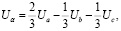 (3)
(3)
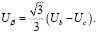 (4)
(4)
Так как линейные напряжения описываются выражениями
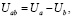 (5)
(5)
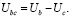 (6)
(6)
Преобразование Кларк для линейных напряжений имеет вид
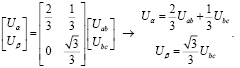 (7)
(7)
Из уравнений электрического равновесия для обмотки статора двигателя в неподвижных координатах (α и β) можно выразить потокосцепление статора [6]:
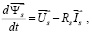 (8)
(8)
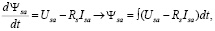 (9)
(9)
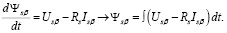 (10)
(10)
Связь потокосцеплений статора и ротора с токами асинхронного двигателя, независимо от выбранной системы координат, можно представить в виде следующих выражений [7, с. 21]:
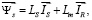 (11)
(11)
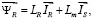 (12)
(12)
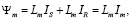 (13)
(13)
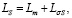 (14)
(14)
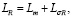 (15)
(15)
где LσS – индуктивность рассеяния статора;
LσR – индуктивность рассеяния ротора;
Lm – индуктивность основного потока (взаимная индуктивность).
Из вышеперечисленных уравнений выражаем уравнение потокосцепления ротора в удобной форме:
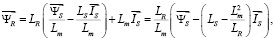 (16)
(16)
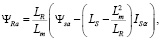 (17)
(17)
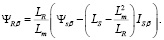 (18)
(18)
Электромагнитный момент, выраженный через потокосцепление статора, описывается следующим выражением [8, с. 53]:
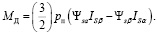 (19)
(19)
Зная электромагнитный момент, можно рассчитать частоту роторной ЭДС по следующей формуле:
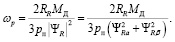 (20)
(20)
Частоту напряжения питания можно вычислить как производную от угла между вращающейся системой координат и неподвижной. Если принять, что ось x вращающейся системы координат сонаправлена вектору потокосцепления ротора, то указанный угол θc можно вычислить как арктангенс отношения проекции вектора потокосцепления ротора на неподвижную ось β к проекции вектора потокосцепления ротора на неподвижную ось α:
ω0эл =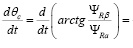
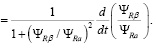 (21)
(21)
Произведя необходимые упрощения, данное выражение примет вид
ω0эл =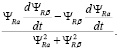 (22)
(22)
Скорость двигателя определяется следующим выражением:
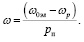 (23)
(23)
Обобщенная система уравнений, описывающих асинхронный электродвигатель, позволяющая вычислить все необходимые параметры для создания бездатчиковых замкнутых систем, как скалярного, так и векторного регулирования, представлена ниже (24).
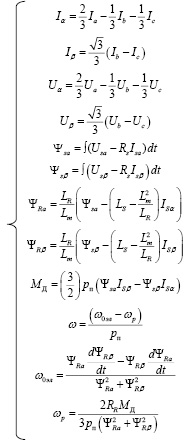 (24)
(24)
Построение имитационной модели наблюдателя
На основании данной системы уравнений была построена модель наблюдателя в программном комплексе Matlab-Simulink, показанная на рис. 1.
На вход полученной модели поступают данные о значении потребляемого электродвигателем тока (Iabc) и линейного напряжения питания (Uabbc) асинхронного электродвигателя. Ко входным величинам применяется преобразование координат, после чего происходит вычисление промежуточных величин, таких как потокосцепление статора, потокосцепление ротора и электромагнитный момент электродвигателя.
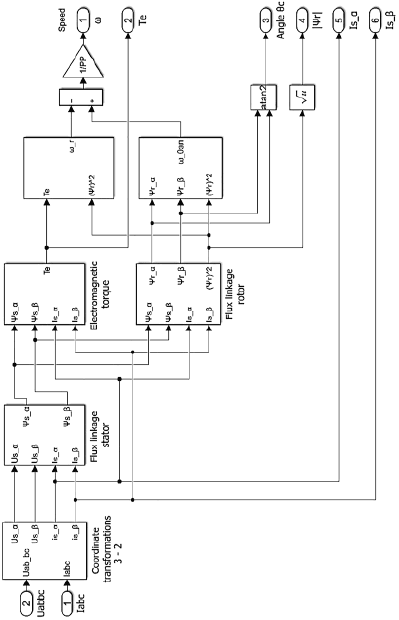
Рис. 1. Модель наблюдателя состояния для систем управления асинхронным электроприводом
Структуры соответствующих вычислительных блоков показаны на рис. 2–4.
На основании вычисленных промежуточных значений происходит вычисление выходных данных, к которым относятся: скорость вращения электродвигателя, электромагнитный момент электродвигателя, угол поворота подвижной системы координат, значение потокосцепления ротора, а также ток статора в неподвижной системе координат.
Показанные блоки и вся модель в целом собраны из простых базовых элементов, аналоги которых есть во многих системах структурного и имитационного моделирования, что не создает проблем при сборке структуры данной модели в других программных комплексах.
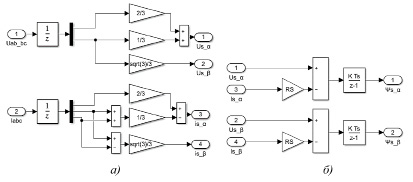
Рис. 2. Структура блока преобразования координат (а) и блока вычисления потокосцепления статора (б)
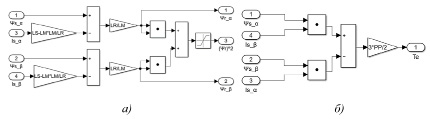
Рис. 3. Структура блока вычисления потокосцепления ротора (а) и блока вычисления электромагнитного момента (б)
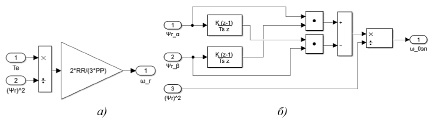
Рис. 4. Структура блока вычисления частоты роторной ЭДС (а) и блока вычисления частоты напряжения питания (б)
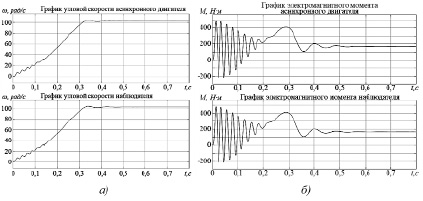
Рис. 5. Графики угловых скоростей модели асинхронного двигателя и наблюдателя (а) и электромагнитных моментов модели асинхронного двигателя и наблюдателя (б)
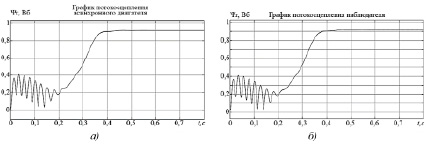
Рис. 6. Графики потокосцеплений роторов модели асинхронного двигателя (а) и наблюдателя (б)
Собранная модель позволяет применять полученный наблюдатель как для построения бездатчиковых систем скалярного регулирования, так и для построения бездатчиковых систем векторного управления.
В связи с тем, что для облегчения дальнейшей работы с моделью наблюдателя она была реализована в виде отдельной подсистемы (Simulink Subsystem), некоторые переменные полученного наблюдателя задаются через параметры (Mask parameters):
RS, RR – активное сопротивление статора и ротора соответственно;
LS – полная индуктивность цепи статора, рассчитанная по формуле (14);
LR – полная индуктивность цепи ротора, рассчитанная по формуле (15);
LM, PP – индуктивность основного потока и число пар полюсов соответственно.
Для демонстрации работы построенной модели наблюдателя состояния асинхронного электродвигателя был выбран крановый электродвигатель МТКН 411-6 на 22 кВт.
На рис. 5–6 показаны результаты имитационного моделирования построенной модели наблюдателя состояния в сравнении с результатами, полученными из блока имитационной модели асинхронного электродвигателя (Asynchronous Machine) из библиотеки Simulink. Из показанных графиков следует, что данные, выдаваемые наблюдателем состояния асинхронного электродвигателя, согласуются с данными, получаемыми из блока имитационной модели асинхронного электродвигателя.
Заключение
Несмотря на то, что предложенная модель наблюдателя строится на упрощенных уравнениях асинхронного электродвигателя, не учитывающих ряд факторов, влияющих на поведение асинхронного электродвигателя при работе в реальных условиях (зависимость коэффициентов от температуры, степень насыщения магнитной цепи, равномерность воздушного зазора), что снижает его точность в реальных системах управления по сравнению с другими вариантами наблюдателей, данный наблюдатель хорошо подходит для разработки, моделирования и анализа бездатчиковых систем управления частотными электроприводами, а также для изучения принципов построения систем векторного управления частотными электроприводами. Это связано с достаточно простой и интуитивно понятной структурой данного наблюдателя, позволяющей интегрировать в структурную или имитационную модель векторного управления отдельный блок наблюдателя, а не использовать данные напрямую от применяемой модели электродвигателя, что, в свою очередь, не только улучшит понимание структуры и работы векторных систем управления, но и оставит возможность модернизировать данный наблюдатель в соответствии с поставленными задачами.



