Работа современного инженера-конструктора тесно связана с компьютером, разработкой цифровых моделей в системах автоматизированного проектирования (САПР). Поэтому начиная с первого курса, уже при изучении таких дисциплин, как «Инженерная графика», «Инженерная геометрия и компьютерная графика», все больше внимания уделяется вопросам 3D-моделирования. В то же время в публикациях многих авторов [1, 2] подчеркивается, что полноценное формирование инженерных компетенций невозможно без изучения теории базового курса начертательной геометрии, проекционного моделирования и конструирования линий, поверхностей и других геометрических объектов. Решение задач дисциплины, требующее сопоставления мысленных образов этих объектов с плоской моделью, развивает пространственное воображение, логическое, критическое мышление. При этом закладываются основы формирования инженерного мышления, полученные знания и навыки помогают в дальнейшем, при работе в САПР, выбирать оптимальный алгоритм формирования 3D-модели, анализировать результат, находить и исправлять ошибки.
Учебный материал легко усваивается студентами при сбалансированном соотношении теории и практики в программе дисциплины, заинтересованности студентов в предмете. Успешность обучения во многом зависит от объема и содержания заданий. Концепция повышения качества образования, а также наблюдаемые в последнее время тенденции к индивидуализации и уровневой дифференциации находят отражение в содержании учебно-методического обеспечения дисциплины. Актуальной становится необходимость насыщения программы более сложными, практико-направленными заданиями. Разработать систему признаков, на основе которой подобрать, классифицировать и ранжировать задачи с элементами, требующими нестандартного подхода к решению, и при этом посильные для студентов разного уровня подготовки, сформировать методический комплекс, позволяющий преподавателю оптимизировать выбор задач при организации учебной деятельности студентов – цель исследования, описанного в данной статье.
Материалы и методы исследования
Для достижения цели:
− проведен обзор публикаций в журналах, материалах конференций, интернет-ресурсов, где рассматриваются методики проведения занятий;
− проанализирован и систематизирован опыт и методический фонд, собранный преподавателями графических дисциплин СПбПУ;
− проанализированы архивы олимпиадных задач по начертательной геометрии и пособия для подготовки к олимпиадам;
− проанализированы новые учебные издания, учебники и задачники прошлых лет.
Информация собрана и обобщена. Определены основные тенденции развития дисциплины, проблемные вопросы, которые следует учитывать в работе:
1. Дисциплина «Начертательная геометрия» в настоящее время, как правило, составляет первый раздел таких дисциплин, как «Инженерная графика», «Инженерная геометрия и компьютерная графика», «Инженерная и компьютерная графика» и т.п.
2. В публикациях обращается внимание на феномен присутствия начертательной геометрии в разных общетехнических и специальных учебных дисциплинах и возможности решения ее методами задач из разных областей техники [3, 4]. Междисциплинарность задач, видимая практическая значимость привлекательна для студентов.
3. Многие авторы предлагают применять САПР и создаваемые с их помощью 3D-модели как наглядные учебные пособия, как инструмент для решения задач, как самостоятельный объект изучения, а также комплексно, ставя сразу несколько из перечисленных целей [5, 6].
4. Выделяются работы, где в качестве инструмента для решения задач используются инструменты конструктивного геометрического моделирования, в частности программа Симплекс. Тематика задач в этом случае может быть значительно расширена, однако для этого требуются серьезные изменения в содержании курса.
5. Олимпиадные задачи в значительной степени различаются по уровню сложности, есть возможность подбора задач, соответствующих сформулированным выше условиям. Условия задач доступны на сайтах сети Интернет, имеются пособия для подготовки. Фонд задач собран преподавателями СПбПУ благодаря участию команды студентов в региональной олимпиаде по начертательной геометрии и опыту подготовки к ней.
6. Выбраны задачники и учебники прошлых лет, отмечены некоторые новые учебные издания, материалы которых могут быть полезны для выполняемой работы.
7. Проанализирован методический фонд, собранный преподавателями СПбПУ. Выбраны задания, имеющие ярко выраженное практическое применение в продолжении курса – при изучении инженерной графики.
8. Во многих работах отмечается, что содержание дисциплины требует пересмотра [7–9]. Предлагается включить в программу дисциплины изучение многомерной начертательной геометрии и элементов высшей математики, больше внимания уделить вопросам моделирования кривых линий и поверхностей, в том числе поверхностей, задаваемых каркасом кривых или точек, что получило широкое практическое применение в промышленных разработках.
9. В целях повышения интереса и мотивации студентов к учебе при решении задач следует обратить внимание на педагогические приемы, учитывающие психологические факторы, такие как рейтинговая система оценивания, интерактивные занятия, технологии геймификации и др. [10].
10. В исследованиях по педагогике [11] рекомендуется при подготовке методического обеспечения дисциплины разрабатывать не отдельные задачи, а комплексы задач по темам.
Результаты исследования и их обсуждение
Общие требования к формированию комплексов в применении к дисциплине «Начертательная геометрия» сформулируем следующим образом:
1. Задачи должны охватывать все изучаемые в теории термины, теоремы и алгоритмы, по возможности – отображать взаимосвязи с другими дисциплинами и возможности практического применения.
2. Задачи должны различаться по виду деятельности и сложности, обеспечивая последовательность изучения от простого к сложному и различные варианты использования в учебном процессе.
3. Количество задач должно быть достаточным для обеспечения возможностей уровневой дифференциации и индивидуализации обучения.
На основе выполненного поиска и анализа информации разработана классификация задач (таблица) и концептуальная модель выбора задач по разным признакам (рис. 1).
Выбираются преимущественно задачи с «нестандартными» элементами в условии, требующими нестандартного подхода к решению, повышенной относительно используемых обычно на занятиях сложности. Тип и количество элементов, которые делают задачу отличной от решаемых в стандартной ситуации и поэтому названных «нестандартными», учитывается в классификации (таблица, п. 2). Наличие нестандартного элемента, как правило, выявляется уже при анализе исходных данных задачи. Если формулировка и рисунок полностью определяют проекции описанных объектов, то считаем исходные данные полными. Есть задачи, в которых дано только описание проблемы и (или) рисунок, который не является геометрической моделью. Это означает, что данное описание сначала нужно «перевести» на язык геометрии и составить проекционную модель и только потом можно приступить непосредственно к решению. Этот аспект учитывается признаком полноты информации об исходных данных.
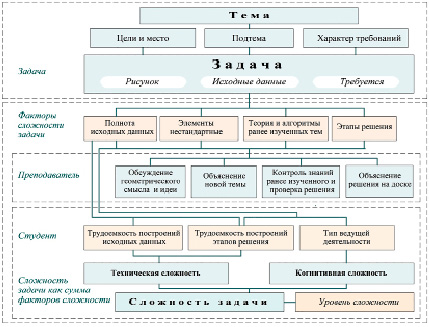
Рис. 1. Концептуальная модель процесса выбора и оценки сложности задачи
Выбор задач. Признаки классификации
|
Классификация задач |
||
|
1 |
По теме занятия |
Темы согласно рабочей программе дисциплины |
|
2 |
По типу нестандартного элемента |
1) нестандартное расположение геометрических фигур 2) нестандартные геометрические фигуры и термины 3) нестандартное требование 4) нестандартное количество решений и возможность разных способов решения 5) нестандартное преобразование 6) практическая направленность задачи |
|
3 |
По количеству нестандартных элементов |
1) не более двух элементов включительно 2) три и более элемента |
|
4 |
По количеству используемых при решении ранее изученных тем и алгоритмов |
1) не более двух тем (или алгоритмов) 2) три и более темы (или алгоритма) |
|
5 |
По количеству этапов решения |
1) от 1 до 5 этапов включительно 2) более 5 этапов |
|
6 |
По полноте информации об исходных данных |
1) присутствует геометрическая модель и (или) однозначно сформулированное словесное описание модели 2) присутствует словесное описание, геометрическая модель отсутствует, рисунка нет, либо он не является геометрической моделью, модель нужно составить |
|
7 |
По характеру требований |
1) на построения и определение взаимного положения фигур (позиционная) 2) на измерения (метрическая) 3) на построения, измерения, преобразования (комплексная) 4) на конструирование: построения по заданным параметрам (конструктивная) |
|
8 |
По ведущей деятельности |
1) репродуктивная 2) алгоритмичная 3) творческая 4) проблемная |
|
9 |
По трудоемкости построений |
Исходные данные: 1) до 5 мин включительно 2) более 5 мин Этапы решения: 1) до 15 мин включительно 2) более 15 мин |
|
10 |
По целям и месту в системе обучения |
1) для иллюстрации при изучении новой темы или алгоритма 2) для актуализации знаний, повторения 3) для совершенствования навыков решения 4) при организации контроля и коррекции знаний учащихся 5) в качестве домашнего задания 6) для обобщения и систематизации изученного материала 7) при подготовке к олимпиадам |
|
11 |
По уровню сложности |
1) легкая 2) средней сложности 3) сложная |
Основные признаки, необходимые для выбора задачи для практического использования – тема и подтема согласно рабочей программе дисциплины (РПД). Заметим, что есть ряд задач, к которым можно обращаться несколько раз, поскольку решение может быть получено разными способами. Кроме того, во многих случаях задача охватывает теорию ранее изученных тем, требует знания нескольких алгоритмов. Как правило, решение такой задачи разбивается на несколько этапов. Все это отражается на трудоемкости решения, то есть времени, необходимом для выполнения построений всех этапов решения. Необходимо учитывать, что скорость решения зависит от многих факторов: уровня подготовленности группы, стиля работы преподавателя, времени суток и т.п. Предугадать все условия практически затруднительно. Поэтому для ранжирования приняты значения, определяющие возможность рассмотрения нескольких задач за время занятия. Немного проще и достаточно точно, по насыщенности рисунка при условии полноты исходных данных, можно оценить трудоемкость построения исходных данных, то есть время, необходимое для вычерчивания проекций данных геометрических фигур.
От того, что именно требуется сделать в задаче, зависит тип задачи согласно традиционному делению задач начертательной геометрии по характеру требований (таблица, п. 7). Вид ведущей деятельности в научных публикациях определяется по-разному [11]. Нами принята следующая классификация. Задачи позиционные или метрические со стандартной формулировкой, полными исходными данными и при наличии у студентов на момент предъявления средств и способов для их решения, под чем понимаем знакомство с необходимой теорией и владение нужными алгоритмами, называем репродуктивными. Как правило, это простые задачи на распознавание и умение воспроизвести известные действия. Если средства для решения у студентов отсутствуют, то есть тема задачи новая, алгоритм решения неизвестен студентам и (или) имеются нестандартные элементы, а решение состоит из нескольких этапов, то задачу считаем творческой. Как правило, к творческим относятся комплексные задачи. Алгоритмической называем задачу, которая решается по алгоритму, повторяющемуся много раз, к этой группе можно отнести, например, задачи на построение проекций линий пересечения поверхностей. И, наконец, проблемной задачей считаем задачу олимпиадного уровня, которая требует всестороннего анализа не только при поиске решения, но и на этапе построения геометрической модели данных объектов. Заметим, что творческая задача, в отличие от проблемной, на более позднем этапе обучения может перейти в разряд репродуктивных или алгоритмических.
Эффективность применения задач тесно связана с целью решения и местом в учебном процессе. Подобрать задачу для использования на том или ином этапе и с определенной целью поможет соответствующий классификационный признак (таблица, п. 10).
Выполнение одного из основных дидактических принципов организации обучения в направлении от простого к сложному требует оценки сложности задачи – показателя, который трактуется педагогами и психологами как «свойство задачи препятствовать успешному ее решению» [11].
Различные подходы к определению сложности учебных заданий показаны в работах Я.А. Микка, М.А. Лепика, Г.А. Балла, В.В. Романова, С.В. Русакова, О.И. Перескоковой, О.Э. Наймушиной, Б.Е. Стариченко и др. [11, 12]. Будем рассматривать сложность как многофакторный показатель, который отражает «число и характер мыслительных операций, необходимых для ее решения нормативным способом» [12]. Исследования авторов статьи [12] О.Э. Наймушиной и Б.Е. Стариченко взяты в качестве основы для разработки системы оценки сложности и уровня сложности задач по начертательной геометрии. Уровень сложности определяется по шкале с тремя градациями. Задача считается легкой, если соответствует уровню узнаваемости, а для решения достаточно знаний основных понятий. Задачи средней сложности требуют размышления, охватывают одну-две темы, выявляют умения применять знания в стандартных ситуациях. Задачи, требующие знания более двух тем и творческого использования этих знаний в нестандартной ситуации, назовем сложными [12].
Уровень сложности определяется с помощью так называемых факторов сложности – компонентов сложности, каждый из которых выражает определенный аспект процесса решения [12]. Факторами могут быть количество и характер мыслительных операций, необходимых для выполнения задания и определяющих время, необходимое для решения, то есть его трудоемкость, количество специальных терминов в условии задачи и т.д. Выбор факторов и алгоритма оценки сложности зависит от специфики дисциплины. На рис. 2 показана зависимость сложности задач по начертательной геометрии от выявленных в процессе исследования факторов.
Графический метод решения существенно влияет на трудоемкость, поэтому рационально использование системы, в которой выделяют две группы факторов сложности. Когнитивная сложность определяется факторами, связанными с мыслительной деятельностью студентов, техническая сложность – сложностью и длительностью техники выполнения задания и факторами, влияющими на трудоемкость [12]. Два вида сложности, как правило, оцениваются в баллах, их сумма определяет сложность задачи. Корректность системы проверяется с помощью статистической обработки результатов решения. На этапе разработки комплекса задач количественная характеристика сложности представляет проблему из-за отсутствия статистики. Поэтому принято решение не определять когнитивную сложность, но оценивать техническую сложность, под которой понимаем затраты времени на вычерчивание исходных данных и выполнение построений всех этапов решения.
С целью помочь преподавателю выбрать задачу для конкретного занятия предлагается также учитывать время, необходимое для разного вида педагогической деятельности (рис. 1). Выбранные факторы отражают элементы практикуемого подхода к проведению занятий и организации процесса решения задачи: выделено время для обсуждения геометрического смысла задачи и идеи решения, время для контроля знаний ранее изученного материала, который может быть проведен в форме опроса или небольшого тестирования при необходимости, и для проверки решения – в случае, если студентам предоставляется возможность решить задачу самостоятельно.
Все данные о задачах собираются в таблице, организованной в соответствии с разработанной классификацией. Преподаватель, готовясь к занятию, может выбрать задачу или несколько задач по любому из критериев с учетом уровня подготовленности группы и методической цели.
Рассмотрим пример задачи, рекомендуемой для рассмотрения на втором или третьем занятии, тема которого – «Моделирование линий. Взаимное положение линий». Условие формулируется следующим образом: Даны три прямые: m, n, k. Требуется построить горизонталь h, пересекающую все три прямые (рис. 2, а). Использованы обозначения: цифры и буквы с индексами «1» – фронтальные проекции точек и линий, с индексами «2» – горизонтальные проекции, x12 – ось проекций.
Задача удовлетворяет требованиям к отбираемым задачам:
1. Совпадающие разноименные проекции прямых – необычны на начальном этапе.
2. Предлагается построить горизонталь, тогда как при таким образом расположенной проецирующей прямой более ожидаемо было бы требование построить фронталь.
3. Прямые m и n пересекаются, точка пересечения имеет совпадающие проекции, значит, принадлежит тождественной плоскости, что определяет новый объект и термин.
4. Задача имеет два решения, решения могут быть получены разными способами.
Этапы построений решения способом, доступным для студентов на рассматриваемом этапе изучения курса, изображены на рис. 2, б–г, и 3, а–д. Как правило, студенты начинают решение с построения фронтальной проекции горизонтали, располагая ее так же, как в решении № 2 (рис. 3, а). Но этот первый шаг часто приводит к неверному решению (рис. 4, а): студенты не обращают внимания на индексы в обозначениях совпадающих проекций прямых. А если обращают, то останавливаются на втором шаге (рис. 3, б), не находя способа провести прямую линию через три точки. Считают, что в условии допущена ошибка или задача не имеет решения. Самостоятельно справляются менее половины от общего количества обучающихся, выбирая в основном другой путь – вариант решения № 1 (рис. 2, б–г). Два решения находят и могут их обосновать еще меньше студентов. На рис. 4 показаны типичные неверные решения.
Таким образом, задача предоставляет широкое поле для обсуждения свойств проекционных моделей. В процессе решения полезно предложить студентам подумать о количестве возможных решений, доказать, что можно построить только две горизонтали, удовлетворяющие условию, и других решений нет. В продолжение темы можно обсудить свойства прямой линии, имеющей совпадающие проекции, поговорить о теореме Дезарга. С методической точки зрения задача интересна еще и потому, что к ней можно вернуться позже: разобрать другой подход к решению при изучении темы «Пересечение прямой и плоскости», убедиться в правильности построений, преобразовав плоскость, образованную прямыми m и n, в проецирующую.
а) б) в) г)
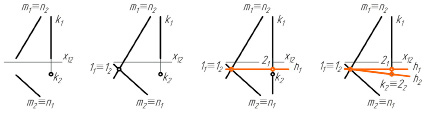
Рис. 2. а – исходные данные; б, в, г – Решение № 1, Этап 1. Шаг 1, Шаг 2, Шаг 3
а) б) в)
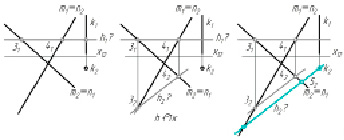
г) д)
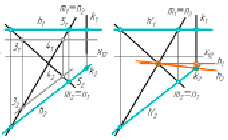
Рис. 3. а, б – Решение № 2, Этап 2. Шаг 1, Шаг 2; в, г – Решение № 2, Этап 3. Шаг 1, Шаг 2; д – 2 решения задачи
а) б) в)
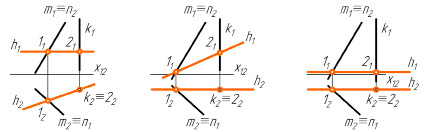
Рис. 4. Типичные неправильные решения студентов
Важна и организация занятий. Необходимо давать студентам возможность самостоятельно находить решение предложенных задач. Преподаватель должен руководить, задавая вопросы, проводя аналогии, так, чтобы обучающиеся активно включались в обсуждение, учились выражать свои мысли, делать оценку своего и чужого решения, выявлять ошибки и осознавать успехи – то есть учиться осознанно, развивая рефлексивные умения, что является залогом успеха в обучении и профессиональном становлении.
Заключение
В работе рассмотрены проблемы организации учебной деятельности студентов, изучающих начертательную геометрию, а также инженерную графику и инженерную геометрию, где начертательная геометрия составляет первый и основополагающий раздел. Представлена работа по формированию методического комплекса задач различной сложности с элементами, требующими нестандартного подхода. Сформулированы классификационные признаки, в соответствии с которыми осуществляется наполнение комплекса. Принципы формирования комплекса, возможности использования и проблемы оценки сложности учебной задачи на этапе разработки методического комплекса задач отражает рассмотренный пример.
Подбирая и классифицируя задачи соответственно поставленным целям, авторы статьи убедились в том, что учебная задача – это не просто и не только средство формирования требуемых компетенций. Выбирая задачу, преподаватель организует учебный процесс, реализует различные методы обучения, дифференцированный и индивидуальный подходы.
Работа призвана упростить и оптимизировать труд преподавателя, наполнить практику преподавания задачами, решение которых будет способствовать активизации интереса к предмету, повышению мотивации к учебе, развитию рефлексивных способностей и инженерного мышления обучающихся.



