Ветропарки работают в нижней части атмосферного пограничного слоя, для которой характерна существенная турбулентность. Турбулентность (Re ≈ 105) может привести к повышенным усталостным нагрузкам ветротурбин и преждевременному выходу их из строя. Для анализа скоростных и турбулентных характеристик воздушного потока необходимо принять во внимание особенности рельефа территории и шероховатость подстилающей поверхности.
Теория аэродинамики одиночной ветротурбины выстроена и хорошо изучена [1; 2] в значительной степени благодаря накопленному опыту аэродинамики воздушных винтов. Ряд исследований посвящен структуре аэродинамических следов отдельных ветротурбин [3-5]. В исследованиях ветропарков и их влияния на атмосферный пограничный слой остается еще ряд не до конца изученных вопросов, например влияние шероховатости поверхности на состояние пограничного слоя атмосферы и аэродинамику ветротурбин. Современные работы в области аэродинамики ветропарков направлены, главным образом, на изучение структуры турбулентных следов ветротурбин и их взаимодействия для поиска оптимальных конфигураций ветропарков [6-8]. Известно [9], что при увеличении шероховатости поверхности происходит изменение структуры пограничного слоя по высоте, что вызвано перемешиванием слоев воздуха, движением потоков импульса и тепла. В связи с этим для поддержания эффективных аэродинамических режимов работы ветропарков необходимо комплексное исследование турбулентных течений в зоне ветропарка с учетом шероховатости подстилающей поверхности.
Натурные исследования атмосферных течений в области ветропарков ограничиваются затратами на дорогостоящие средства измерений и диагностики, невозможностью изменения условий эксперимента. В этой связи большую популярность получают методы вычислительной гидродинамики (от англ. Computational Fluid Dynamic, CFD) на базе математического моделирования и численных подходов, обеспечивающих выполнение экспериментов в контролируемых условиях. К числу таких методов относятся моделирование течений на основе осредненных по Рейнольдсу уравнений Навье-Стокса (RANS), а также метод вихреразрешающего моделирования (LES). Результаты расчетов CFD-моделей многократно демонстрировали хорошее соответствие с измерениями в аэродинамических трубах [1; 2; 4]. В настоящей работе для моделирования турбулентности авторы применяют метод RANS на основе осредненных по Рейнольдсу уравнений Навье-Стокса по причине меньших требований к вычислительным ресурсам (по сравнению с LES-подходом, как, например, в [8]) и удовлетворительной согласованности полученных результатов с экспериментальными данными. RANS-подход демонстрирует приемлемую точность расчетов при корректной настройке параметров модели [10]. Для этого авторы применяют модифицированную модель турбулентности k – ε с уточненными значениями кинетической энергии турбулентности и скорости ее диссипации, что позволит достоверно учесть влияние сети ветротурбин на атмосферный пограничный слой, а также оценить эффективность управления ветротурбинами в текущих условиях.
Цель работы – комплексное исследование аэродинамики атмосферного пограничного слоя в области ветропарка на основе применения методов математического моделирования и численного анализа, оценка влияния шероховатости подстилающей поверхности на динамику ветропарка и скорость восстановления аэродинамических следов ветротурбин.
Материал и методы исследования
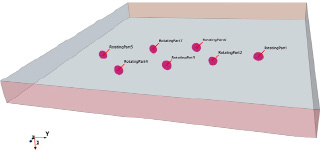
Объектом исследования в данной работе выступает часть Ульяновского ветропарка в виде семи ветротурбин марки V126-3.45 номинальной мощностью 3,5 МВт. На рисунке 1 показаны цифровая 3D-модель ветротурбины V126-3.45 и расчётная область исследуемой части ветропарка для численных экспериментов, включающая семь ветротурбин.
Вращающиеся поверхности ветротурбин (Rotating Part) выделены цветом. Высота ветротурбин составляет 100 м, длина лопасти – 62 м. Размеры ветрового туннеля составили 4*4 км2.
В работе рассматривается течение воздушного потока в зоне ветропарка для условий нейтрального атмосферного пограничного слоя. Математическая формулировка включает уравнения движения для составляющих скорости движения воздушного потока, уравнение состояния и граничные условия. Для анализа турбулентных потоков в области ветропарка решено применять RANS-подход. Для связи характеристик осредненного течения с добавочными напряжениями трения используется предложенная авторами расширенная модель турбулентности k – ε с уточненными значениями кинетической энергии турбулентности и скорости ее диссипации. Для описания пристеночных областей (поверхность лопасти ветроколеса, подстилающая поверхность на нижней стенке) применялся метод пристеночных функций.
|
|
|
|
а) |
б) |
Рис. 1. Цифровая 3D-модель ветротурбины V126-3.45 (а), расчётная область исследуемой части ветропарка (б)
В рамках k – ε модели турбулентности коэффициент турбулентной вязкости определяется по следующему выражению:
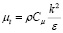, (1)
где μt – коэффициент турбулентной вязкости, Па∙с; Cμ – безразмерная константа турбулентности, принимается равной 0,09; k – кинетическая энергия турбулентности, м2/с2; ε – вязкая диссипация кинетической энергии турбулентности, м2/с3.
Транспортные уравнения для кинетической энергии турбулентности k и скорости диссипации кинетической энергии ε приведены в следующем виде:
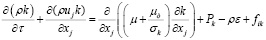, (2)
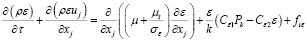, (3)
где ρ – плотность среды, кг/м3; xj – координаты x, y, z, м; uj – компоненты осредненной скорости ветра u, v, w, м/с; τ – время, с; μ ‒ динамическая вязкость среды, Па∙с; μt – турбулентная вязкость, Па∙с; Pk – генерация энергии турбулентности, м/с3; fik – источниковый член, описывающий влияние ветротурбин на генерацию кинетической энергии, кг/(м∙с3); fiε – источниковый член, описывающий влияние ветротурбин на диссипацию турбулентной кинетической энергии в потоке, кг/(м∙с4).
Принимается, что константы, используемые в k – ε модели турбулентности, имеют значения: Cε1 = 1,44; Cε2 = 1,92; σk = 1; σε = 1,3. Выражения для определения источниковых членов fik и fiε были получены на основе анализа дифференциальных уравнений Рейнольдса [15] и идентификации влияющих факторов.
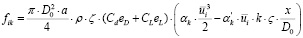, (4)
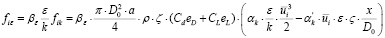, (5)
где D0 – диаметр ветроколеса, м; a – плотность ветротурбин на территории ветропарка, м2/м3;ζ – коэффициент заполнения ветропарка, определяется расположением и количеством ветротурбин; ϛ – коэффициент сглаживания для перераспределения действия силы в пространстве; СL – коэффициент подъемной силы лопасти, СD – коэффициент сопротивления лопасти; eD eL – единичные векторы вдоль соответствующих сил; αk – доля средней кинетической энергии потока, которая преобразовалась в турбулентную кинетическую энергию из-за действия ветротурбин;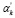 
доля диссипации турбулентной кинетической энергии из-за каскадного переноса энергии в аэродинамическом следе ветротурбин.
Значение констант модели αk,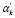 
, βε проводилось с использованием алгоритмов оптимизации и серии тестовых вычислительных экспериментов для наилучшего приближения к результатам измерений [1; 2; 8].
Для проведения вычислительных экспериментов использовалось коммерческое программное обеспечение Star-CCM+ Academic Pack. Эксперименты выполнялись на компьютерной модели в масштабе 1:100. Для распространения результатов модели на реальный ветропарк использовались подходы из теории подобия. Численное исследование выполнено на сгенерированной расчетной сетке с многогранными ячейками. Общее количество расчетных ячеек многогранной сетки составило 14,9 млн штук.
Граничные условия настраивались по стандартной схеме расчета [5] с уточнениями значения постоянной Кармана æ, которую принимали равной 0,39 на лопастях ветроустановки и 0,42 на подстилающей поверхности. Скорость ветра профильная, описываемая степенным законом для летнего периода. На уровне ступицы ветротурбины величина скорости составила 8 м/с. Атмосферная турбулентность задана 5%. Все ветротурбины ориентированы перпендикулярно направлению потока, количество оборотов составило 10 об./мин. согласно режимному графику.
Результаты исследования и их обсуждение
Выполнена серия расчетов при различных значениях шероховатости подстилающей поверхности z. Шероховатость характеризует тип поверхности: z = 0,003 м для плоских равнинных поверхностей; z = 0,03 м для открытых аграрных территорий, редколесья; z = 0,3 м для лесных массивов.
Моделирование ветропарка производилось на достаточном времени для обеспечения квазистационарных условий течения и статистической сходимости результатов. Адекватность полученного численного решения подтверждается сходимостью расчетов, невязки без колебаний, ограничением по величине. Верификация результатов производилась по известным литературным и экспериментальным данным [1; 2; 8]. Погрешность расчетов не превысила 8%. Общее время счета задачи составило 90 секунд, шаг по времени задавался dτ = 0,01c.
В ходе расчета были получены поля осредненных и мгновенных величин: скорости и интенсивности турбулентности.
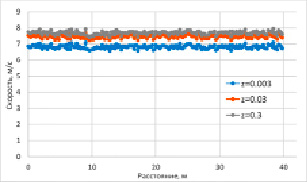
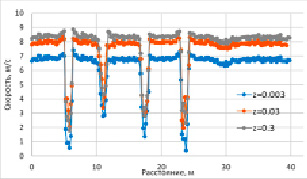
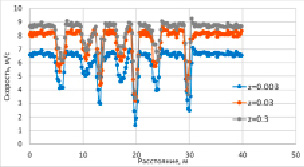
По мере обтекания очередной ветротурбины наблюдается местное падение скорости. На рисунке 2 показаны рассчитанные контуры усредненной по времени скорости потока на уровне ступицы ветротурбин при различной шероховатости подстилающей поверхности.
Попадая в область вращения ветроколеса, характер движения воздушного потока изменяется. При обтекании ветротурбин происходит турбулизация потока, аэродинамические следы имеют форму винтовой спирали. Отмечена извилистость следов ветряных турбин. Отбирая энергию набегающего потока, ротор ветротурбины тормозит его, и в аэродинамическом следе образуется характерный провал скорости, кроме этого, в данной зоне наблюдались наибольшие значения уровня турбулентности потока (рис. 2, 3).
Результаты расчетов демонстрируют неосесимметричное распределение профиля средней скорости и, следовательно, среднего сдвига в следе турбины. Это объясняется неоднородным (логарифмическим) профилем скорости набегающего потока.
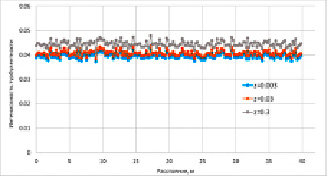
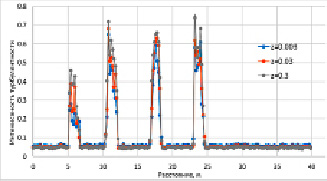
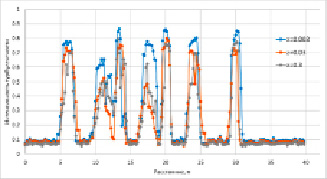
Характер движения воздушных потоков на территории ветропарка нестационарный и турбулентный. Результаты в части расчета интенсивности турбулентности воздушного потока в окрестности ветротурбин при различной шероховатости подстилающей поверхности приведены на рисунке 3.
В случаях с более высокой шероховатостью подстилающей поверхности следы восстанавливались несколько быстрее с расстоянием вниз по течению. Так, при шероховатости подстилающей поверхности z = 0,3 профиль скорость восстанавливается на 18% быстрее, чем при наименьшем рассматриваемом значении шероховатости z = 0,003. Увеличение шероховатости подстилающей поверхности способствовало увеличению интенсивности турбулентности и вертикальному перемешиванию воздушных потоков, что приводило к более быстрому восстановлению аэродинамических следов ветротурбин. Помимо более высокой интенсивности турбулентности, извилистые следы в нестабильных случаях также могут объяснить более плавные профили следа.
а)
б)
в)
Рис. 2. Усредненная по времени скорость воздушного потока на уровне ступиц ветротурбин при различной шероховатости подстилающей поверхности: до ветротурбин (а), после первых четырех по потоку ветротурбин (б), после всех ветротурбин на расстоянии 2D (D – диаметр ветроколеса) (в)
а)
б)
в)
Рис. 3. Интенсивность турбулентности воздушного потока на уровне ступиц ветротурбин при различной шероховатости подстилающей поверхности: до ветротурбин (а), после первых четырех по потоку ветротурбин (б), после всех ветротурбин на расстоянии 2D (D – диаметр ветроколеса) (в)
Однако при сложной конфигурации ветропарка повышенный уровень турбулентности может приводить к чрезмерным механическим нагрузкам на элементы нижестоящих ветротурбин, а дефицит скорости потока не позволит работать ветротурбинам в режиме максимальной выработки. Поэтому восстановление аэродинамического следа до состояния невозмущенного потока имеет ключевое значение для эксплуатации крупных ветропарков. В рассматриваемом случае расположение ветротурбин оптимальное, так как попадания ветротурбин в области высокой турбулентности воздушных масс не наблюдалось. Дефицит скорости является наибольшим вблизи ветротурбины и становится меньше по мере того, как след расширяется и увлекает окружающий воздух. Тем не менее эффект следа все еще заметен даже на расстояниях, достигающих 11D (D-ветроколеса).
Заключение
В работе выполнено моделирование и численное исследование атмосферного пограничного слоя в окрестности части Ульяновского ветропарка, состоящего из семи ветротурбин. В работе использовались усредненные по Рейнольдсу уравнения Навье-Стокса RANS (Reynolds-averaged Navier–Stokes) для расчета, замыкание системы уравнений реализовано с использованием модифицированной k – ε модели турбулентности.
RANS-подход позволил весьма точно смоделировать аэродинамические процессы в области ветропарка. Выявлено, что увеличение шероховатости подстилающей поверхности способствует увеличению интенсивности турбулентности и приводит к более быстрому восстановлению аэродинамических следов ветротурбин. Результаты, полученные при моделировании, находятся в приемлемом согласии с известными литературными и экспериментальными данными. Погрешность расчетов не превысила 8%.
В будущих исследованиях авторы намерены рассмотреть влияние осадков и многофазных воздушных потоков на эффективность работы ветропарков. Понимание аэродинамики воздушных потоков в области ветропарков позволит корректно прогнозировать производство электроэнергии, а также разрабатывать эффективные стратегии управления для снижения механических нагрузок на элементы ветротурбин.