В современных мультиагентных системах управления химическими производствами играет важную роль эффективное распределение задач между роботами-лаборантами [1-3].
Цель исследования: разработка теории решения гарантированных задач управления мультиагентной системой коллектива роботов-лаборантов.
В данной работе рассматривается проблема оптимизации времени, выделяемого на выполнение конкретных задач, и его влияние на общий экономический эффект. Учитывая, что частота выполнения процессов, таких как взятие проб для лабораторного анализа, напрямую влияет на эффективность управления [4], встает задача поиска оптимального времени загрузки роботов-лаборантов. Также рассматриваем зависимости между частотой выполнения задач и увеличением экономического эффекта, особенно при больших областях вариации времени загрузки. При этом случайные возмущения и недетерминированные характеристики технологических процессов требуют новых подходов к управлению коллективом роботов-лаборантов [5; 6].
Материалы и методы исследования
В работе использовались методы теории оптимизации, математической статистики. Методический подход к формализации задачи оптимизации временных характеристик системы управления роботами-лаборантами. Ограниченность ресурсов времени загрузки роботов-лаборантов позволяет ставить задачу оптимизации времени их работы, которая при ограниченном диапазоне вариации времени загрузки роботов-лаборантов может формулироваться как задача линейного программирования [7].
Результаты исследования и их обсуждение
В продолжение исследований в [8] рассмотрим постановку и решение задачи гарантированного линейного программирования со случайными добавками к коэффициентам.
Рассмотрим задачу оптимизации, целевую функцию которой запишем в виде:
Q(U) = (CO + vC1)U, (1)
где v – случайная величина с известной плотностью вероятности
ω(v), CO = (CO1 ,...,COn),
C1 = (C11,..., C1n), U = (u1,...,un),
а технологические требования представлены следующим образом:
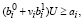
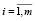 , (2)
, (2)
где 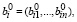
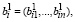 – случайные величины с известными плотностями распределения ωi(vi), ai – постоянная величина.
– случайные величины с известными плотностями распределения ωi(vi), ai – постоянная величина.
Дальнейшее исследование сосредоточено на постановке и решении задачи гарантированного линейного программирования с учетом случайных добавок к коэффициентам. Целью исследования является нахождение вектора u*∈U, минимизирующего математическое ожидание функции (1):
M[Q(u*)] = min M[(C0 + vC1)U], (3)
вероятность Р выполнения условий (2) не ниже заданных значений σi:
P[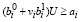 ] ≥ σi
] ≥ σi
и ui ≥ 0, i = 1,2,...,n.
Задачу (3) с учетом линейности целевой функции (1) сформулируем следующим образом: найти вектор u*∈U, при котором функция (1) стремится к минимуму:
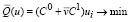 , (4)
, (4)
где v – математическое ожидание случайной величины v, и выполнение ограничений:
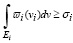 , (5)
, (5)
Ei = [vi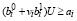 ],
], 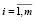 , (6)
, (6)
ui ≥ 0. (7)
Предложенная формулировка задачи позволяет свести ее к эквивалентной задаче линейного программирования: найти вектор управления u, обеспечивающий минимальное значение целевой функции и удовлетворение технологических ограничений:
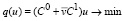 , (8)
, (8)
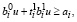 (9)
(9)
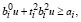 (10)
(10)
где 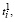
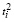 определяются из соотношений:
определяются из соотношений:
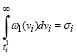 , (11)
, (11)
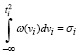 , (12)
, (12)
Ui ≥ 0, 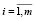 .
.
Рассмотрим следующую вспомогательную лемму.
Лемма 1. Пусть множества 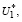
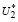 определяются следующими неравенствами:
определяются следующими неравенствами:
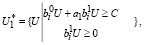 (13)
(13)
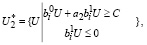 (14)
(14)
где а1, а2, С – постоянные величины.
Объединение множеств 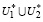 тождественно множеству U*,
тождественно множеству U*,
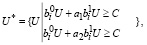 (15)
(15)
Доказательство.
Для того, чтобы доказать тождественность U*=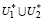 , необходимо доказать следующее утверждения: для любого U* справедливо:
, необходимо доказать следующее утверждения: для любого U* справедливо:
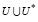 ⇒U∈
⇒U∈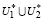 , (16)
, (16)
U∈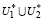 ⇒ U∈U*. (17)
⇒ U∈U*. (17)
При этом, т.к. выполнение (16) очевидно, остается доказать (17).
Не уменьшая общность, будем далее полагать, что
а1 ≤ а2. (18)
1. Рассмотрим вначале случай, когда
С – 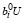 < 0. (19)
< 0. (19)
А. Пусть при этом U ∈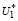 . Докажем, что это U∈U*, т.е. удовлетворяет условиям (15). Т.к. первое неравенство (15) совпадает с первым неравенством (13), необходимо доказать выполнение второго неравенства (15).
. Докажем, что это U∈U*, т.е. удовлетворяет условиям (15). Т.к. первое неравенство (15) совпадает с первым неравенством (13), необходимо доказать выполнение второго неравенства (15).
Пусть а1 не отрицателен, т.к. с учетом (18) имеет место
0 ≤ а1 ≤ а2 (20)
и с учетом (19)
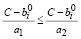 < 0. (21)
< 0. (21)
Из второго неравенства (13) и (21) имеем:
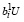 ≥ 0 >
≥ 0 >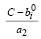 ,
,
что равносильно выполнению второго неравенства (19).
Пусть теперь а1, а2 удовлетворяют соотношениям а1 < 0 ≤ а2, т.е. с учетом (19):
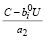 < 0 <
< 0 <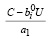 . (22)
. (22)
Из второго неравенства (13) и (22) при этом имеем:
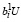 ≥ 0 ≥
≥ 0 ≥ 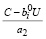 ,
,
что равносильно выполнению второго неравенства (15).
Пусть, наконец, а1, а2 удовлетворяют соотношениям а1 ≤ а2 < 0, т.е. с учетом (19):
0 <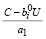 ·
·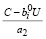 . (23)
. (23)
Из первого неравенства (13) с учетом (23) имеем:
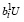 ≤
≤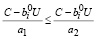
или 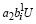 ≥ C –
≥ C – 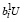 , что равносильно выполнению второго неравенства (15).
, что равносильно выполнению второго неравенства (15).
Таким образом, во всех случаях при выполнении (19) справедливо
U∈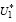 ⇒ U∈U*. (24)
⇒ U∈U*. (24)
Б. Пусть теперь условие (19) выполнено, но U∈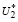 . Докажем, что и в этом случае U∈U*, т.е. удовлетворяется неравенство (15). Т.к. в этом случае второе неравенство (15) совпадает с первым неравенством (18), необходимо доказать выполнение первого неравенства (19).
. Докажем, что и в этом случае U∈U*, т.е. удовлетворяется неравенство (15). Т.к. в этом случае второе неравенство (15) совпадает с первым неравенством (18), необходимо доказать выполнение первого неравенства (19).
Пусть значение а1 не отрицательно, т.е. с учетом (21) имеют место соотношения (20) и (21). При этом из первого неравенства (14) с учетом (13) имеем:
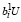
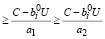
или 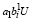 ≥ C –
≥ C – 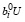 , что равносильно выполнению неравенства (15).
, что равносильно выполнению неравенства (15).
Пусть для а1, а2 удовлетворяют соотношениям а1 < 0 ≤ а2 и (22).
При этом из второго неравенства (14) с учетом (22) имеем:
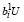 ≤ 0 <
≤ 0 < 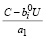
или 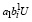 > C –
> C – 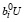 , что соответствует выполнению первого неравенства (15).
, что соответствует выполнению первого неравенства (15).
Пусть, наконец, имеет место неравенство а1 ≤ а2 < 0 (23). При этом из второго неравенства (14) и (23) имеем:
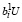 ≤ 0 ≤
≤ 0 ≤ 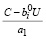
или 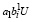 ≥ C –
≥ C – 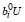 ,
,
т.е. неравенство (15) выполнено.
Таким образом, при выполнении (19) имеем:
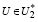 ⇒U∈U*. (25)
⇒U∈U*. (25)
Из выполнения (24), (25) имеем:
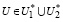 ⇒U∈U*. (26)
⇒U∈U*. (26)
2. Рассмотрим случай, когда:
С – 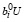 > 0. (27)
> 0. (27)
А. Пусть справедливо соотношение:
0 ≤ а1 ≤ а2. (28)
В этом случае система неравенств (14) противоречива, т.е. множество 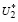 пусто и для доказательства тождественности необходимо доказать, что
пусто и для доказательства тождественности необходимо доказать, что
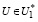 ⇒U∈U*. (29)
⇒U∈U*. (29)
Из условий (27), (28) имеем:
0 < 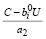
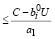 . (30)
. (30)
Пусть 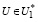 , в этом случае из первого неравенства (13) имеем с учетом (30)
, в этом случае из первого неравенства (13) имеем с учетом (30)
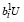
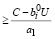 ·
· 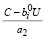 ,
,
т.е. второе условие (15) выполнено.
Так как первое условие (15) совпадает с первым неравенством (13), утверждение (29) выполнено.
Б. Пусть справедливо соотношение:
а1 < 0 ≤ а2. (31)
В этом случае из (13) с учетом (27), (31) имеем:
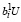
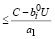 < 0,
< 0, 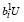 ≥ 0,
≥ 0,
т.е. система (13) противоречива и множество 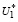 – пусто.
– пусто.
Из (14) с учетом (27), (31) следует
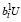
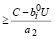 > 0,
> 0, 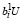 ≤ 0,
≤ 0,
т.е. система (14) также противоречива и множество 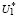 , так же как и
, так же как и 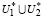 , пусто.
, пусто.
Из (14) следует, что множество U* также в этом случае пусто, т.к. неравенства (15) противоречивы:
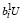
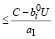 < 0,
< 0, 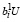
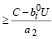 > 0.
> 0.
В. Наконец рассмотрим случай
а1 ≤ а2 < 0. (32)
В этом случае система неравенств (13) противоречива, т.е. множество U* пусто и для доказательства тождественности 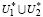 и U необходимо доказать, что
и U необходимо доказать, что
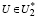 ⇒U ∈ U*. (33)
⇒U ∈ U*. (33)
Исходя из условий (32) и (27), имеем:
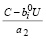
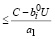 . (34)
. (34)
Пусть 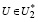 , и в этом случае из первого неравенства (14) и (34) имеем:
, и в этом случае из первого неравенства (14) и (34) имеем:
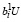
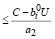
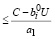 ,
,
или 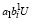 ≤ C –
≤ C – 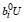 ,
,
т.е. первое условие (15) выполнено.
Так как второе условие (15) совпадает с первым условием (14), которое выполнимо по предположению U∈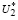 , утверждение (33) выполнимо.
, утверждение (33) выполнимо.
Из (29) и (33) следует, что при выполнении (27) имеет место:
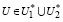 ⇒U ∈ U*. (35)
⇒U ∈ U*. (35)
Из (26), (35) следует, что при всех значениях (C – 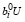 ) условия (16), (17) выполняются.
) условия (16), (17) выполняются.
Лемма 1 доказана.
Теорема 1.
Задача гарантированного линейного программирования со случайными добавками к коэффициентам (4) – (7) тождественна эквивалентной задаче (8), (12).
Доказательство.
Так как целевые функции задач (4)-(7) и (8)-(12) совпадают, для доказательства тождественности этих задач достаточно доказать тождественность условий (5), где t определяется условиями (9), (10).
Пусть параметры 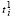 ,
, 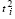 определяются (11), (12). Технологическое неравенство (2) может быть, очевидно, записано в виде системы неравенств:
определяются (11), (12). Технологическое неравенство (2) может быть, очевидно, записано в виде системы неравенств:
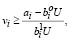 если
если 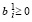 , i = 1,2,...,m,
, i = 1,2,...,m,
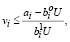 если
если 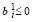 , i = 1,2,...,m.
, i = 1,2,...,m.
При этом (6) может быть сформулировано в следующем виде:
Ei = (vi | vi ≥ 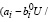
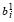 U)), если
U)), если 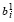 U ≥ 0
U ≥ 0
и vi ≤ 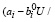
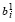 U), если
U), если 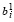 U < 0. (36)
U < 0. (36)
В том случае, если для 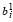 U ≥ 0 выполняется неравенство
U ≥ 0 выполняется неравенство
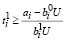 , (37)
, (37)
где 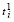 определяет (5), имеет место:
определяет (5), имеет место:
σi =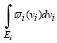 = Pi (U), (38)
= Pi (U), (38)
т.е. условие (5) выполняется при 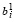 U ≥ 0.
U ≥ 0.
Аналогично, если для 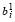 U ≤ 0 выполняется неравенство
U ≤ 0 выполняется неравенство
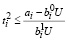 , (39)
, (39)
где 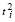 определяется (12) имеет место:
определяется (12) имеет место:
σi =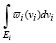 = Pi (U), (40)
= Pi (U), (40)
т.е. условие (5) выполняется и в этом случае.
Таким образом, из (38), (40) и (37), (39) следует, что условия (6), (9) выполняются, если в эквивалентной задаче выполняется система неравенств:
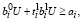
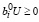 .
.
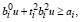
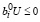 .
.
Согласно лемме 1 объединение множеств 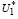 , определяемого (13), и
, определяемого (13), и 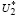 , определяемого (14), тождественно множеству U, определяемому (9), (10).
, определяемого (14), тождественно множеству U, определяемому (9), (10).
Теорема 1 доказана.
Таким образом, задача гарантированного линейного программирования со случайными добавками к коэффициентам сводится к детерминированной задаче линейного программирования вида (8)-(12). Как следует из (9), (10), эквивалентная задача характеризуется наличием вдвое большего числа ограничений, чем исходная задача. При этом в ограничении (9), (10) величины 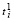 ,
, 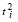 являются константами, определяемыми однократно из условий (11), (12).
являются константами, определяемыми однократно из условий (11), (12).
Рассмотрим сопутствующую задачу гарантированного линейного программирования.
Будем называть сопутствующей задаче (4)-(7) следующую задачу линейного программирования: найти 2m-мерный вектор y = (y1,...,y2m), при котором принимает максимальное значение целевая функция:
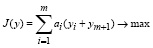 (41)
(41)
и выполняются условия: (42)
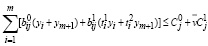
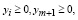 i =1,...,m, (43)
i =1,...,m, (43)
где 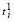 ,
, 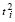 определяются соотношениями (11), (12).
определяются соотношениями (11), (12).
Теорема 2.
Пусть U* – решение задачи гарантированного линейного программирования (4)-(7), а 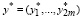 – решение сопутствующей задачи (41)-(43). В этом случае имеет место:
– решение сопутствующей задачи (41)-(43). В этом случае имеет место:
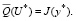 (44)
(44)
Доказательство.
Для задачи гарантированного линейного программирования (4)-(7) эквивалентная задача (8)-(12) может быть переформулирована в следующем виде: найти n-мерный вектор U = (U1,...,Un), при котором принимает минимальное значение целевая функция:
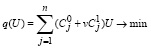 (45)
(45)
и удовлетворяются ограничения:
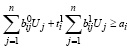 , i =1,...,m, (46)
, i =1,...,m, (46)
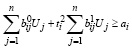 , i =1,...,m, (47)
, i =1,...,m, (47)
Uj ≥ 0, j =1,...n, (48)
где 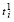 ,
, 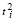 определяются соотношениями (11), (12).
определяются соотношениями (11), (12).
Так как, согласно теореме 1, эквивалентная задача (8)-(12) (или, это то же самое, (45)-(48)) тождественна задаче гарантированного линейного программирования (4)-(7), имеет место:
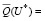
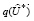 , (49)
, (49)
где U* – решение задачи гарантированного линейного программирования (4)-(7); 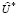 – решение эквивалентной задачи (45)-(48).
– решение эквивалентной задачи (45)-(48).
Запишем эквивалентную задачу (45)-(48) в следующем виде: найти n-мерный вектор U = (U1,...,Un), при котором принимает максимальное значение целевая функция:
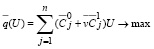 (50)
(50)
и удовлетворяются ограничения:
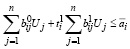 , i =1,...,m, (51)
, i =1,...,m, (51)
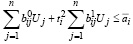 , i =1,...,m, (52)
, i =1,...,m, (52)
Uj ≥ 0, j =1,...n
и выполняются (11), (12),
где 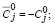
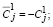
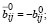 (53)
(53)
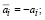
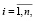
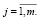
При этом очевидно, что решения 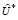 задачи (45)-(48) и задачи (50)-(53) совпадают и вследствие известного соотношения:
задачи (45)-(48) и задачи (50)-(53) совпадают и вследствие известного соотношения:
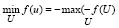 (54)
(54)
имеем q(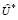 ) = – q(
) = – q(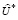 ).
).
Двойственная к (50)-(52) задача может быть сформулирована в виде: найти 2m-мерный вектор y =(y1,...,y2m ) , при котором принимает минимальное значение целевая функция:
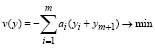 , (55)
, (55)
удовлетворяются ограничения:
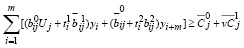 , yi ≥ 0, i=1,2,...,2m (56)
, yi ≥ 0, i=1,2,...,2m (56)
и выполняются соотношения (11), (12), имеет место:
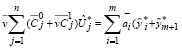 , (57)
, (57)
где 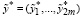 – решение задачи (55)-(57).
– решение задачи (55)-(57).
Используя (51), сформулируем задачу (55)-(57) в следующем виде: найти 2m-мерный вектор y =(y1,...y2m), при котором принимает минимальное значение:
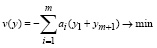 (58)
(58)
и удовлетворяются ограничения
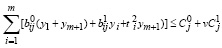 , yi ≥ 0, i=1,2,...,2m. (59)
, yi ≥ 0, i=1,2,...,2m. (59)
и соотношения (11), (12).
Из сравнения задачи (41)-(43) и задачи (58)-(59) следует, что эти задачи отличаются лишь целевой функцией, при этом
J(y) = – v(y).
В этом случае решение y* задачи (41)-(43) и решение задачи (55)-(57) (или, то же самое, задачи (58)-(59)) совпадают, и в соответствии с (54) имеем:
J(y*) = – v(y*). (60)
Из (57), (54) и (60) имеем
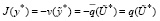 . (61)
. (61)
Из (61) и (49) следует
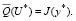
Теорема 2 доказана.
Таким образом, сопутствующая задача гарантированного линейного программирования со случайными добавками к коэффициентам сводится к детерминированной задаче линейного программирования вида (8)-(12).
Заключение
Разработанная теория решения гарантированных задач позволяет обеспечить управление работой мультиагентной системы роботов-лаборантов на химических производствах с заданной вероятностью выполнения технологических и технических требований. Результаты, полученные в данном исследовании, подтверждают результаты исследований технологического процесса производства обесфторенных фосфатов.



