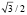Интерполяционные формулы Лагранжа, Ньютона, Стирлинга и иных при использовании большого числа узлов интерполяции на всем отрезке [a; b] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей используется кусочно-полиномиальная интерполяция. В этом случае весь отрезок [a; b] разбивается на частичные отрезки, и на каждом из них функцию f(x) заменяют приближенно полиномом невысокой степени.
Один из способов интерполирования на всем отрезке [a; b] является интерполирование сплайнами [1]. Сплайн представляет собой кусочно-полиномиальную функцию, определенную на отрезке [a; b] и имеющую на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – сходимость и устойчивость вычислительного процесса.
В качестве примера рассмотрим один из наиболее распространенных случаев – интерполирование функции кубическим сплайном [2].
Пусть на отрезке [a; b] задана непрерывная функция f(x).
Введем разбиение отрезка:
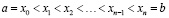(1)
и обозначим yi = f(xi), i = 0,1,2,…,n.
Интерполяционный кубический сплайн [3], соответствующий данной функции f(x) и узлам интерполяции (1), будет определяться функцией S(x), удовлетворяющей следующим условиям:
1) на каждом отрезке [xi–1; xi ], i = 0,1,2,…,n. функция S(x) является кубическим многочленом; 2) функция S(x), а также ее первая и вторая производные непрерывны на отрезке [a; b]; 3) S(xi) = f(xi), i = 0,1,2,…,n. соответствует условию интерполирования [4].
Целью статьи является сравнительный анализ результатов приближенного вычисления с точными данными при использовании операции интерполирования методом кубического сплайна. Сравнительный анализ погрешностей и расхождений производится на основе визуализации расчетных зависимостей в виде графиков найденных интерполяционных полиномов.
Материал и методы исследования
Для примера нахождения и построения кубического сплайна [5] рассмотрим функцию f(x) = sinx. Используем два метода получения приближенных значений для указанной функции. В первом случае реализуем построение кубического сплайна вручную, а полученную систему уравнений решим методом обратной матрицы в числовом редакторе Excel. Во втором случае используем реализацию построения кубического сплайна с помощью языка программирования Python.
Первый метод
Определим для указанной функции три узла интерполирования. На каждом узле составим кубический сплайн, используя таблицу значений функции f(x) = sinx, x ∈ [0; π / 2].
Значения функции f(x) = sinx, x ∈ [0; π / 2]
|
x |
0 |
π / 6 |
π / 3 |
π / 2 |
|
sin x |
0 |
1/2 |
|
1 |
Уравнения сплайнов для трех узлов интерполирования с учетом исходных данных имеют вид:
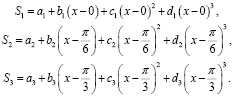(2)
Коэффициенты ai, bi, ci, di с учетом трех условий прохождения через узловые точки и с учетом преобразований имеют вид:
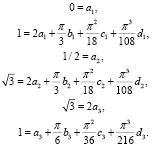(3)
Также необходимо выполнение следующих условий.
1. В стыках между сплайнами должна обеспечиваться гладкость. В узлах не должно быть изломов. Отсюда следует, что в узлах интерполирования должны быть одинаковыми первые производные соседних сплайнов, соответствующих системе уравнений:
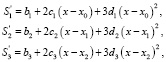(4)
Сплайны S1 и S2 стыкуются в точке x1 = π / 6. После подстановки в систему уравнений (4) значения точки х1, а также данных таблицы равенство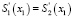 
принимает вид:
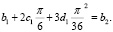(5)
Аналогично со сплайнами S2 и S3, которые стыкуются в точке x2 = π / 3.
Рис. 1. Коэффициенты a1, b1, c1, d1, a2, b2, c2, d2 и a3, b3, c3, d3 в числовом редакторе Excel
Равенство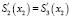 
принимает вид:
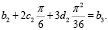(6)
2. В узлах, где стыкуются сплайны, должна быть одинаковой кривизна соседних сплайнов. Это означает равенство вторых производных, соответствующих системе уравнений:
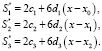(7)
Сплайны S1 и S2 стыкуются в точке x1 = π/6, а сплайны S2 и S3 – в точке x2 = π / 3. После подстановки в систему уравнений (7) значения точки x1, а также данных таблицы получаем:
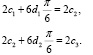(8)
3. Необходимо задать поведение сплайнов на левой и правой границах, то есть в точках x0 и x3. Для этого необходимо задать нулевую кривизну (нулевые значения вторых производных). В точке x0 = 0: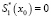 
, а в точке x2 = π / 2: 
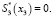После подстановки в систему уравнений (3) с учетом преобразований получаем:
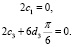(9)
В результате получили систему уравнений (3), (5), (6), (8), (9) с 12 неизвестными.
Такую систему удобно решить в числовом редакторе Excel методом обратной матрицы [6]. Найденные искомые коэффициенты представлены на рисунке 1.
Второй метод.
Используем для построения кубического сплайна высокоуровневый язык программирования Python [7]. Программный код должен быть написан таким образом, чтобы можно было выбрать любую функцию для построения кубического сплайна. Для нашего случая будем рассматривать также функцию f(x) = sinx на тех же узлах интерполирования. Программный код представлен на рисунках 2, 3. В структуру кода добавлены комментарии, поясняющие алгоритм построения кубического сплайна.
Результаты исследования и их обсуждение
После запуска программы в интегрированной среде IDLE пользователь должен ответить на вопрос, что именно он хочет сделать. При этом пользователю доступны варианты с вводом любого набора точек функции и вводом любой функции. В примере на рисунке 4 выбрана функция f(x) = sinx. Далее вводятся значения аргументов по порядку, которые будут соответствовать каждому из трех узлов интерполирования. Следующим шагом программа строит три интерполяционных многочлена третьей степени и подставит в них посчитанные коэффициенты.
Сравнительный анализ коэффициентов, полученных в результате реализации программного кода на языке Python, и коэффициентов, полученных в результате решения системы уравнений методом обратной матрицы в числовом редакторе Excel, показывает наличие расхождений при вычислениях.
При расчетах методом обратной матрицы в числовом редакторе Excel были получены следующие значения коэффициентов:
a1 = 0,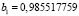 
,
c1 = 0,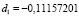 
a2 = 0,5,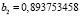 
,
, 
,
, 
,
, 
.
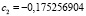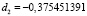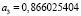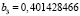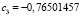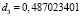Рис. 2. Листинг реализации программного кода на языке программирования Python
Рис. 3. Листинг реализации программного кода на языке программирования Python
Рис. 4. Демонстрация работы программы с построенными многочленами третьей степени
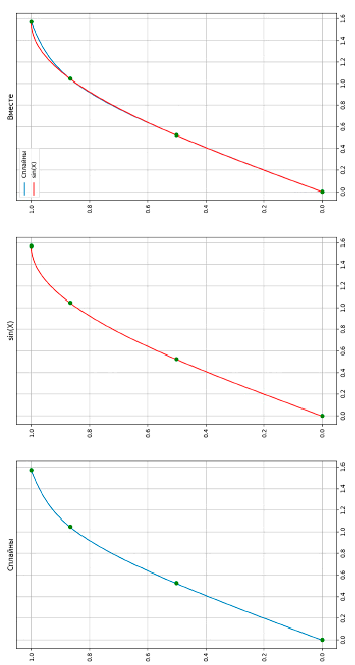
Рис. 5. Графики интерполяционных многочленов, функции f(x) = sinx и их наложения друг на друга
При вычислении коэффициентов с помощью реализации метода интерполирования на языке программирования Python получились следующие значения:
a1 = 0,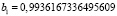 
,
c1 = 0,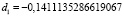 
,
,
,
,
,
,
,
,
.
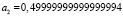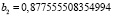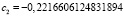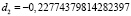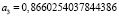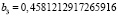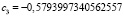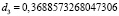По полученным данным можно построить график найденных интерполяционных полиномов в виде кубического сплайна и график функции. На рисунке 5 показаны график функции f(x) = sinx, график интерполяционных многочленов и график наложения функций друг на друга.
На рисунке 3 видно, что график точного значения функции и значения, рассчитанного приближенным методом с помощью интерполирования кубическими сплайнами, расходятся.
Вывод
В результате работы, выполненной в статье, можно сделать вывод о том, что различные методы расчета приближенных значений для функций дают разные результаты и в любом методе имеются свои погрешности и расхождения. Но так или иначе реализация метода интерполирования сплайнами с использованием элементов Индустрии 4.0 [8, 9] с помощью языка программирования Python дает более точные данные, которые подтверждаются наименьшим расхождением графиков. Также к плюсам второго метода исследования можно отнести меньшую трудозатратность за счет полностью автоматических расчетов программой.