Для молекулярной биотехнологии необходима разрешающая способность до 10-16 как технических устройств и математических моделей обработки с оценкой плотностей вероятностей пересечения разбросов априорных (начальных) и апостериорных (после опыта) экспериментальных данных [1, 2]. Для обеспечения такой разрешающей способности выявлено возможное усиление сигналов с помощью рамановской спектроскопии с применением графена и кремниевых поверхностных вертикальных нановолокон при комбинации различных наночастиц металлов Ag, Au, Cu с использованием плазмонных эффектов [3, 4]. Наиболее перспективным методом увеличения разрешающей способности является использование взаимозависимостей (корреляции) между многомерными параметрами при обработке большого количества статистических данных рамановской спектроскопии [5, 6]. Применяя гипотезу Байеса об умножении взаимозависимых (корреляционных) вероятностей Pi / Pic, можно получить общую вероятность P0 = ∏ Pi / Pic появления событий [5]. Однако для большого количества параметров получить взаимозависимые вероятности практически невозможно, а также затруднительно составить и решить многомерную систему до 81 уравнений. Поэтому для того, чтобы применить гипотезу Байеса для большого количества параметров, необходимо математически преобразовать все взаимозависимые (корреляционные) параметры в независимый (некорреляционный) вид, и тогда можно использовать гипотезу Байеса для независимых вероятностей Pi в целях вычисления общей вероятности появления независимых событий P0 = ∏ Pi.
Цель работы – разработка математического инструментария на основе компьютерных технологий для повышения чувствительности идентификации наночастиц серебра.
Материалы и методы исследования
Для проведения исследования были выбраны полиэфирные волокна, на которые был нанесен 11%-й раствор коллоидного серебра. Математическая обработка данных рамановских спектров текстильных волокон проводилась с использованием прикладной программы Matchcad.
Вероятность соприкосновения эллипсов статистического разброса интенсивностей одного пика рамановского спектра волокон с наночастицами и без наночастиц серебра при зависимых (корреляционных) данных будет выглядеть при решении системы уравнений как в векторно-матричной форме эллипсов, применяемой в работах [7, 8], так и в аналитической:
, 
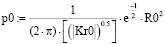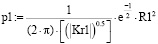, (1)
где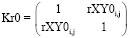 
, 
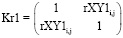– корреляционные матрицы данных эллипса разброса интенсивности пиков рамановского спектра без наночастиц и с наночастицами серебра соответственно;
,
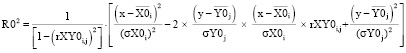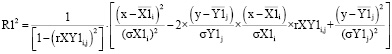– эквивалентные радиусы эллипсов разброса значений пика рамановского спектра
Решение уравнений (1) в виде графического изображения p0 и p1 плотности вероятностей пересечения эллипсов интенсивностей пиков рамановских спектров волокон без наночастиц и с наночастицами серебра с корреляцией двумерных параметров X,Y представлено на рисунке 1.
Точность решения нелинейных уравнений по R0 и R1 для волокон без наночастиц и с наночастицами серебра составляет: f(v0,v1) = 5,458183058222525∙10-15, g(v0,v1) = 9,223526074702766∙10-18. Эквивалентные радиусы эллипсов при решении имеют значения: R0=2,650146690664009, R1=2,6501466906640103.
Плотность вероятностей пересечения эллипсов разбросов данных оценивается при таком решении: p0=0,00676493265273759, p1=0,01395994530203525. Из результатов решения уравнений видно, что R0 и R1 практически не различаются в пределах точности решения системы уравнений, тогда как значения решения p0 и p1 плотности вероятностей пересечения эллипсов по R0 и R1 различаются значительно – на 2 порядка.
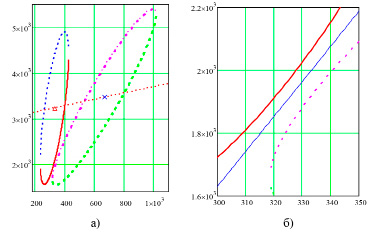
Рис. 1. Графическое изображение пересечения эллипсов распределения рамановских спектров полиэфирных волокон с наночастицами серебра и без наночастиц: а) – общий вид пересечения эллипсов распределения; б) – фрагмент зоны пересечения
Так как решение уравнений (1) не дает достаточной разрешающей способности по p0 и p1, то в рамках данного исследования предложено преобразовать математические модели с наночастицами серебра и без наночастиц в некоррелированный вид с одновременным решением системы уравнений. Преобразование в некоррелированные данные с использованием специальной матрицы будет иметь следующий вид:
, 
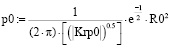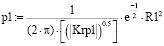, (2)
где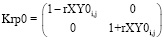 
, 
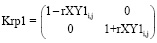– матрицы преобразования корреляционных в некорреляционные данные эллипса разброса интенсивности пиков рамановского спектра для волокон без наночастиц и с наночастицами;
,
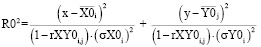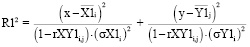– эквивалентные радиусы эллипсов
разброса значений пика рамановского спектра для волокон без наночастиц и с наночастицами серебра соответственно.
При решении уравнений (2) при привязке распределения данных к оси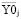 
– – 
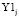для p1=1,961857350956933∙10-9 были получены результаты:
f(v0, v1) = –8,566236531471608∙10-15, g(v0, v1) = –1,3439058138006006∙10-17;
R0 = 6,21119148401521, R1 = 6,21119148401521;
p0 = 9,50708084190474∙10-10, p1 = 1,961857350956933∙10-9.
Анализ этого решения показывает, что по сравнению с непреобразованными данными точность решения повышается, радиусы эллипсов увеличиваются в 2,5 раза и плотности вероятностей пересечения эллипсов уменьшаются до 10-10. Однако p0 и p1 плотности вероятностей пересечения эллипсов для R0 и R1 различаются значительно – на 2 порядка.
Вариант решения уравнений (2) при привязке к нулевой оси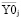 
=0 – – 
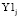=0 дает следующие результаты:
f(v0, v1) =–8,562907845112253-15,
g(v0, v1) = 0,00000000000000000∙100;
R0 = 6,2099845877792195,
R1 = 6,2099845877792195;
p0 = 9,5786092391055∙10-10,
p1 = 1,976617771551228∙10-9.
Ввиду значительного различия эквивалентных радиусов (почти на 2 порядка) следует искать неточности или ошибки в математических моделях.
В первую очередь необходимо проверить выражения (2) на наличие корреляционных взаимозависимостей. Проведенный анализ показал, что в математическом выражении p0 имеется корреляционная зависимость |Krp0|=1 – rXY02, а должна быть некорреляционная зависимость в виде |Krp0|=1, где rXY0=0, так как выражения p0 и R0 уже преобразованы в некорреляционный вид, в знаменателе p0 осталось непреобразованное |Krp0|. Таким образом, в ходе проведения данного исследования было установлено, что в математическом выражении p0 и p1 не должно быть корреляционных зависимостей |Krp0| = 1 – rXY02 и |Krp1|=1 – rXY12, а должны быть некорреляционные зависимости в виде |Krp0|=1 и |Krp1|=1, и соответственно предложена следующая структура уравнений:
, 
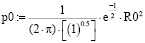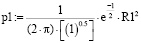(3)
Графическое изображение p0 и p1 (3) вероятности пересечения эллипсов интенсивностей пиков рамановских спектров волокон с наночастицами и без наночастиц при привязке эллипсов распределения данных к оси MENY0j – – MENY1j показано на рисунке 2.
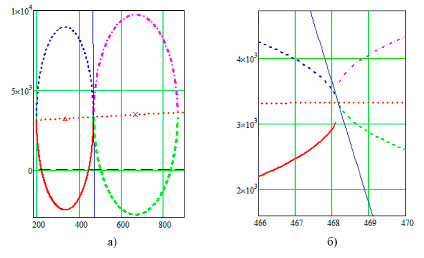
Рис. 2. Графическое изображение пересечения эллипсов распределения данных пиков рамановских спектров полиэфирных волокон с наночастицами серебра и без наночастиц с преобразованием двумерных параметров X,Y в некорреляционный вид: а) – общий вид пересечения эллипсов распределения; б) – фрагмент зоны пересечения
Решение системы уравнений (3) дает результат:
f(v0, v1) = –8,566236531471608∙10-15,
g(v0, v1) = –1,3439058138006006∙10-17;
R0 = 6,21119148401521,
R1 = 6,21119148401521;
p0 = 6,676033594918151∙10-10,
p1 = 6,676033594918175∙10-10.
По результатам этого решения видно, что по сравнению с преобразованными данными (2) точность решения такая же, радиусы эллипсов одинаковые и плотности вероятностей пересечения эллипсов практически одинаковые. Плотности вероятностей p0 и p1 пересечения эллипсов для R0 и R1 также практически не различаются.
Для варианта решения системы уравнений по (3) при привязке к нулевой оси MENY0j=0 – – MENY1j=0 дает результат:
f(v0, v1)=–8,562907845112253∙10-15,
g(v0, v1)=0,00000000000000000∙100;
R0=6,2099845877792195,
R1=6,2099845877792195;
p0=6,726262049965901∙10-10,
p1=6,726262049965924∙10-10.
Результаты исследования и их обсуждение
Результаты решения 81 уравнения исследуемой задачи по пикам от i = 0…8 до j = 0…8 математически преобразованных некоррелированных статистических данных рамановских спектров полиэфирного волокна с концентрацией наночастиц серебра 11% с использованием программы Mathcad показаны на рисунках 3, 4.
Вычисление общего значения суммы логарифмов достоверности по матрице QL (рис. 4) с концентрацией наночастиц серебра 11% при преобразовании в некоррелированный вид для 81 уравнения представлено уравнениями:
, 
, 
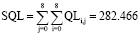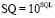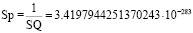. (4)
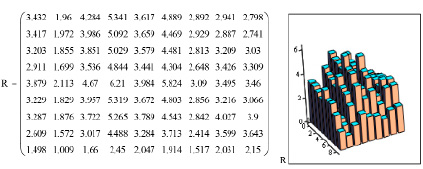
Рис. 3. Матрица эквивалентных радиусов пересечения эллипсов распределения рамановских спектров полиэфирных волокон с концентрацией наночастиц серебра 11%
Результаты вычисления по (4) были проверены по произведению плотностей вероятностей:
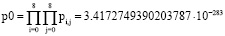. (5)
Результаты вычислений общей плотности вероятностей по сумме логарифма достоверности (4) незначительно отличаются от результата вычислений по произведению плотностей вероятностей (5) всего лишь в третьем знаке Sp = 3,419∙10-283 и p0 = 3,417∙10-283 десятичной базы степенного выражения.
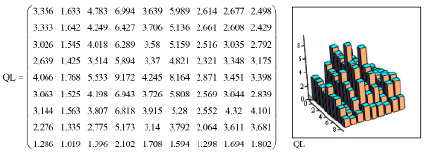
Рис. 4. Матрица достоверности пересечения эллипсов распределения рамановских спектров полиэфирных волокон с концентрацией наночастиц серебра 11% и без наночастиц
Для более точной проверки результатов вычисления (4) и (5) плотностей вероятностей непосредственно используем уравнение преобразования p по сумме квадратов эквивалентных радиусов эллипсов распределения рамановских спектров Ri,j:
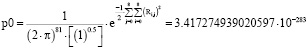. (6)
Проверка еще большей точности получения общей плотности вероятностей по произведению плотностей вероятностей и по сумме квадратов эквивалентных радиусов эллипсов проведена непосредственно при решении системы уравнений отдельно по pφ:
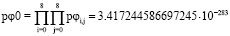. (7)
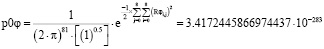. (8)
Выводы
В работе разработан математический метод преобразования корреляционных статистических данных в некоррелированный вид при одновременном решении системы уравнений по R0 и R1 с получением плотностей вероятностей p0 и p1 по R0 и R1 с обязательной заменой корреляционных составляющих: |Kr0|=1-rXY02 и |Kr1|=1-rXY12 – на некорреляционные: |Kr0|=1 и |Kr1|=1.
Этот метод позволяет увеличить чувствительность идентификации наночастиц серебра до 10283 раз и, следовательно, повысить разрешающую способность метода для концентрации наночастиц серебра 11% за счет применения гипотезы Байеса для умножения плотностей вероятностей.
Для повышения точности проверки результатов вычисления плотностей вероятностей непосредственно было использовано уравнение преобразования p0 по сумме квадратов эквивалентных радиусов эллипсов распределения рамановских спектров Ri,j. Здесь результат показывает сходимость баз уравнений в 12-м десятичном знаке.
Для повышения точности решение системы уравнений было осуществлено отдельно по плотности вероятностей pφ. Результат показывает сходимость баз уравнений pφ0 и p0φ в 12-м десятичном знаке (выражения 7 и 8), а уравнений p0 и pφ0 (выражения 5 и 7) – только в 4-м десятичном знаке. Это обусловливает необходимость дополнительного проведения исследований составления и решения системы многомерных корреляционных уравнений по плотностям вероятностей pφ.