В настоящее время методы машинного обучения [1] находят широкое применение при решении проблем в самых разных сферах человеческой деятельности: в медицине [2], в нефтегазовой сфере [3], в энергетике [4] и др. К одному из методов машинного обучения относится регрессионный анализ [5, с. 30]. Выбор линейной функции регрессии для описания функционирования исследуемого явления или процесса лишь в редких случаях приводит к адекватным результатам. Поэтому возникает необходимость в выборе и оценивании нелинейных форм связи между переменными. В работах [6, 7] автором предложены модульные линейные регрессии, в которых регрессорами выступают объясняющие переменные, преобразованные с помощью операции модуль. А например, в [8] рассмотрены неэлементарные линейные регрессии (НЛР), в которых пары объясняющих переменных преобразуются с помощью бинарных операций min и max. Для оценивания модульных регрессий и НЛР с помощью метода наименьших квадратов (МНК) [9] в [6–8] были разработаны специальные алгоритмы.
Цель исследования состоит в разработке новых структурных спецификаций регрессионных моделей на основе слияния модульных регрессий и НЛР, а также в разработке алгоритма их оценивания с помощью МНК.
Материал и методы исследования
Рассмотрим модульную линейную по факторам регрессию с двумя объясняющими переменными [6, 7] вида:
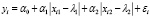, i = 1,n, (1)
где n – объем выборки; yi – i-е значение объясняемой переменной y; xi1, xi2 – i-е значения объясняющих переменных x1 и x2; α0, α1, α2, λ1, λ2 – неизвестные параметры; εi – i-я ошибка аппроксимации. Эта модель относится к нелинейным по оцениваемым параметрам.
Известно [7], что оптимальные МНК-оценки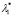 
и 
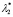параметров λ1 и λ2 модульной регрессии (1) принадлежат промежуткам 
, 
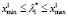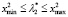, где 
, 
, 
, 
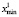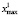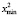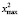– минимальные и максимальные значения переменных x1 и x2. В связи с этим алгоритм «OLS-mod» приближенного МНК-оценивания модульной регрессии (1) состоит из 3 следующих шагов.
Шаг 1. Найти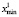 
, 
, 
, 
.
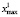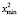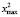Шаг 2. На сторонах прямоугольника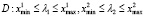 
выбрать равномерно p точек, с помощью которых внутри области D сформировать сеть из (p + 2)2 точек.
Шаг 3. Перебирая все точки сформированной сети, оценить все возможные регрессии (1) с помощью МНК и выбрать из них уравнение с минимальной величиной суммы квадратов остатков.
Чем больше величина p, тем ближе полученные с помощью алгоритма «OLS-mod» МНК-оценки к оптимальным.
Рассмотрим неэлементарную линейную по факторам регрессию (НЛР) [8] с двумя объясняющими переменными и бинарной операцией min вида:
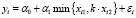, i = 1,n, (2)
где k – неизвестный параметр;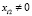 
, i = 1,n.
Известно, что оптимальная МНК-оценка k* параметра k НЛР (2) принадлежит промежутку kнижн ≤ k* ≤ kверхн, где
kнижн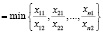 
,
kверхн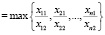 
.
Поэтому алгоритм «OLS-min» приближенного МНК-оценивания НЛР (2) формулируется следующим образом.
Шаг 1. Найти kнижн, kверхн.
Шаг 2. На промежутке kнижн ≤ k ≤ kверхн выбрать равномерно р точек.
Шаг 3. Перебирая все точки промежутка, оценить все возможные НЛР (2) с помощью МНК и выбрать из них уравнение с минимальной величиной суммы квадратов остатков.
Используя вместо объясняющих переменных в НЛР (2) модульные и неэлементарные конструкции, получим 4 новые спецификации регрессионных моделей:
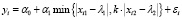, i = 1,n, (3)
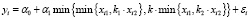, i = 1,n, (4)
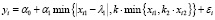, i = 1,n, (5)
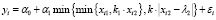, i = 1,n, (6)
где k1, k2– неизвестные параметры.
Структура каждой из моделей (3) – (6) схожа со структурой двухслойной нейронной сети: второй скрытый слой содержит бинарную операцию min, а в первом скрытом слое для каждой переменной комбинируются операция min и модуль. Поэтому назовем модели (3) – (6) двухслойными НЛР с двумя переменными. Как видно, каждая из этих моделей имеет по 5 неизвестных параметров и обобщает НЛР (2).
Стоит отметить, что двухслойная НЛР (4) по внешнему виду схожа с так называемой вложенной кусочно-линейной регрессией [10], оцениваемой с помощью метода наименьших модулей. Разница между ними в том, что в модели (4) присутствуют дополнительные неизвестные параметры k, α0, α1.
Аналогично, используя вместо объясняющих переменных в модульной регрессии (1) модульные и неэлементарные конструкции, получим еще 4 новые спецификации регрессионных моделей:
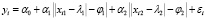, i = 1,n, (7)
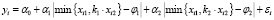, i = 1,n, (8)
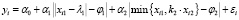, i = 1,n, (9)
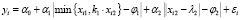, i = 1,n, (10)
где φ1, φ2 – неизвестные параметры.
Также будем называть модели (7) – (10) двухслойными НЛР с двумя переменными. Во втором их скрытом слое содержатся операции модуль, а в первом – операции min и модуль. Каждая из этих моделей имеет уже по 6 неизвестных параметров.
Введем основанный на алгоритмах «OLS-mod» и «OLS-min» универсальный алгоритм «OLS-mod&min» приближенного МНК оценивания двухслойных НЛР (3) – (10).
Шаг 1. В зависимости от выбранной модели определить области возможных значений неизвестных параметров на первом скрытом слое. При этом возможна одна из следующих четырех ситуаций:
1) если переменные x1 и x2 преобразуются операцией модуль, то область
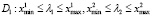; (11)
2) если переменная x1 преобразуется операцией модуль, а переменная x2 – min, то
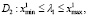kнижн ≤ k2 ≤ kверхн; (12)
3) если переменная x1 преобразуется операцией min, а переменная x2 – модуль, то
D3: kнижн ≤ k1 ≤ kверхн,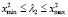 
; (13)
4) если переменные x1 и x2 преобразуются операцией min, то
D4: kнижн ≤ k1 ≤ kверхн, kнижн ≤ k2 ≤ kверхн. (14)
В одном из этих прямоугольников сформировать сеть точек размера (p + 2)×(p + 2).
Шаг 2. Используя сформированную на первом слое сеть, для каждой ее точки сформировать в зависимости от формы модели области возможных значений неизвестных параметров на втором скрытом слое. Пусть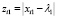 
, i = 1,n, если на первом слое выбрана операция модуль для x1; 
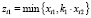, i = 1,n, если на первом слое выбрана операция min для x1; 
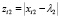, i = 1,n, если на первом слое выбрана операция модуль для x2; 
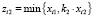, i = 1,n, если на первом слое выбрана операция min для x2. Возможна одна из следующих двух ситуаций.
1. Если выбрана одна из моделей (3) – (6), то каждой точке сформированной на предыдущем шаге сети при условиях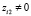 
, i = 1,n поставить в соответствие промежуток kнижн ≤ k ≤ kверхн, где
kнижн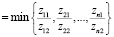 
,
kверхн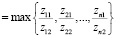 
,
на котором выбрать равномерно p точек. Перебирая все (p + 2)3 точек полученного трехмерного массива, оценить все возможные НЛР с помощью МНК и выбрать из них модель с минимальной величиной суммы квадратов остатков.
2. Если выбрана одна из моделей (7) – (10), то каждой точке сформированной на предыдущем шаге сети поставить в соответствие область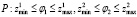 
, где 
, 
, 
, 
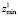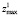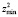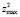– минимальные и максимальные значения переменных z1 и z2, в которой сформировать сеть точек размера (p + 2)×(p + 2). Перебирая все (p + 2)4 точек полученного четырехмерного массива, оценить все возможные НЛР с помощью МНК и выбрать из них регрессию с минимальной величиной суммы квадратов остатков.
К сожалению, идентификация областей неизвестных параметров на первом скрытом слое по формулам (11) – (14) в алгоритме «OLS-mod&min» гарантирует нахождение близких к оптимальным МНК-оценок при большом p не для всех из моделей (3) – (10). Покажем далее, что такая гарантия дается только для регрессий (7) – (10).
Рассмотрим двухслойную модульную модель с одной переменной вида:
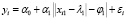, i = 1,n. (15)
Пусть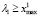 
. Возьмем с этого промежутка случайным образом два любых различных числа, например λ1 = λ#, λ1 = λ# + Δ, где Δ – разница между этими числами. Тогда модель (15) в этих точках принимает формы:
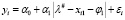, i = 1,n, (16)
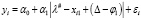, i = 1,n. (17)
Если в (17) переобозначить величину (Δ – φ1) любой переменной, то получим модель (16). Из этого следует, что выбор любой точки с промежутка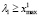 
не меняет величину суммы квадратов остатков регрессии (15) в точке оптимума.
Пусть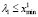 
. Также возьмем с этого промежутка два любых числа λ1 = λ# и λ1 = λ# + Δ. Тогда модель (15) в этих точках принимает формы:
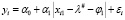, i = 1,n, (18)
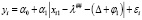, i = 1,n. (19)
Если в (19) переобозначить величину (Δ + φ1) любой переменной, то получим модель (18). Следовательно, выбор любой точки с промежутка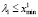 
не влияет на величину суммы квадратов остатков регрессии (15) в точке оптимума. Таким образом, имеет смысл оценивать модель (15) только при 
.
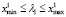Рассмотрим двухслойную неэлементарную модель с одной переменной вида:
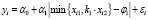, i = 1,n.(20)
Пусть k1 ≥ kверхн. Тогда модель (20) принимает форму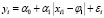 
, i = 1,n. Из этого следует, что выбор любой точки с промежутка k1 ≥ kверхн не меняет величину суммы квадратов остатков регрессии (20) в точке оптимума.
Пусть k1 ≤ kнижн. Возьмем с этого промежутка случайным образом два любых различных числа, например k1 = k#, k1 = k# ∙ Δ, Δ > 0. Тогда модель (20) в этих точках принимает формы:
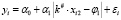, i = 1,n, (21)
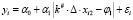, i = 1,n. (22)
Если в (22) вынести за знак модуля Δ и переобозначить величины α1∙Δ и φ1/Δ любыми переменными, то получим модель (21). Следовательно, выбор любой точки с промежутка k1 ≤ kнижн не влияет на величину суммы квадратов остатков регрессии (20) в точке оптимума. Таким образом, имеет смысл оценивать модель (20) только при kнижн ≤ k1 ≤ kверхн.
Представленные рассуждения позволяют сделать вывод, что оптимальные оценки параметров первого скрытого слоя двухслойных НЛР (7) – (10) принадлежат промежуткам (11) – (14). Поэтому, чем больше выбрано значение p, тем ближе полученные с помощью алгоритма «OLS-mod&min» МНК-оценки моделей (7) – (10) к оптимальным.
Результаты исследования и их обсуждение
Для проведения вычислительного эксперимента были использованы статистические данные из источника [11, с. 478] о сменной добыче угля на одного рабочего y (в тоннах), мощности пласта x1 (в метрах) и уровне механизации работ x2 (в процентах), характеризующие процесс добычи угля в 10 шахтах.
Сначала по этим данным с помощью МНК была построена линейная регрессия:
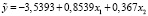, (23)
затем с использованием программы МОДУЛИР-1 модульная регрессия (1):
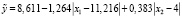,(24)
после чего с использованием программы НЕЭЛИН НЛР (2) с бинарной операцией min
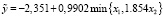. (25)
Коэффициенты детерминации R2 регрессий (23) – (25) равны соответственно 0,8116, 0,8629 и 0,8149.
Предложенный алгоритм «OLS-mod&min» был реализован в виде скрипта на языке hansl пакета Gretl. Сначала с помощью этого скрипта были оценены двухслойные НЛР (3) – (6) с бинарной операцией min на втором слое при p = 50:
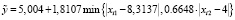, (26)
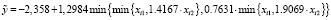, (27)
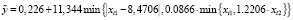, (28)
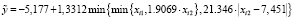. (29)
Коэффициенты детерминации НЛР (26) – (29) равны соответственно 0,935916, 0,814875, 0,936727, 0,932029.
Затем с помощью скрипта были оценены двухслойные НЛР (7) – (10) с операцией модуль на втором слое при p = 50:
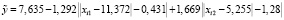, (30)
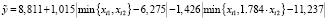, (31)
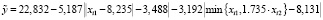, (32)
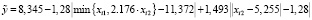. (33)
Коэффициенты детерминации НЛР (30) – (33) равны соответственно 0,974875, 0,965205, 0,909793, 0,976162.
Заключение
В работе с использованием бинарной операции min (max) и операции модуль предложено 8 новых спецификаций регрессионных моделей, названных двухслойными НЛР. Разработан алгоритм их приближенного оценивания с помощью МНК. Успешно проведен вычислительный эксперимент, в ходе которого почти все новые модели, кроме (27), по качеству аппроксимации оказались лучше известных регрессий. При этом точнее оказались двухслойные НЛР с модулем на втором слое.