Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В настоящее время при проектировании и разработке сложных систем, процесс функционирования которых может быть описан с помощью методов теории массового обслуживания, зачастую применяется ряд упрощений, связанных в первую очередь с отсутствием (или значительным усложнением) соответствующих математических моделей неклассических систем массового обслуживания (СМО).

Одними из наиболее распространенных упрощений, применяемых при решении задач прикладного и теоретического характера, являются, по всей видимости, допущения об одинаковой производительности каналов и простейшем (пуассоновском) характере потоков.

При этом вполне очевидно, что во многих реальных системах приборы могут обладать различной интенсивностью обслуживания, а потоки зачастую носят неординарный характер (то есть поступающие в систему заявки могут содержать два и более требований на обслуживание). В качестве элементарного примера СМО такого типа можно привести парикмахерскую, в которой мастера, в зависимости от компетенций, могут обладать различной производительностью, в то же время клиенты (то есть заявки) могут приходить как по одному, так и группами. Очевидно, что в данном случае с прикладной точки зрения упрощения допустимы, а моделирование сложной системы со смешанными потоками нецелесообразно. Однако, к примеру, для компьютерных или телекоммуникационных систем, связанных с обработкой больших данных, требуется более высокая расчетная точность и понимание закономерностей работы СМО такого типа.

В настоящее время в исследованиях отечественных и зарубежных авторов рассмотрены различные модификации систем с каналами различной производительности, в том числе с упорядоченным входом [1], делением и слиянием требований [2], ненадежными приборами [3], катастрофами [4] и др. Функциональным особенностям систем с неэквивалентными каналами посвящены работы [5, 6]. В них показано, что в условиях управления пуассоновскими потоками СМО с неэквивалентными приборами могут быть эффективнее, чем классические системы с одинаковыми каналами. В [7] рассмотрены системы с приборами одинаковой производительности, функционирующие в условиях неординарных потоков. Несмотря на явный прикладной интерес, исследований, посвященных системам с неэквивалентными каналами, функционирующим в условиях смешанных потоков, в научной литературе, по всей видимости, на текущий момент не представлено. В настоящей работе предпринята попытка изучения некоторых функциональных особенностей и закономерностей поведения СМО такого типа.

Объектом исследования являются модели систем массового обслуживания с каналами различной производительности, функционирующие в условиях смешанных потоков.

Целью исследования является сравнительный анализ эксплуатационных характеристик систем массового обслуживания с каналами одинаковой и различной производительности в условиях смешанных потоков.

Материалы и методы исследования

Рассмотрим двухканальную СМО без функции накопления очереди, на вход которой поступает поток заявок интенсивности λ, λ > 0. Интенсивности обслуживания первого и второго приборов равны соответственно μ1 и μ2, μ1, μ2 > 0 (если производительности устройств различны, будем полагать что 0 < μ1 < μ2).

В условиях смешанного потока в систему могут поступать как одинарные, так и групповые заявки (в случае двухканальной системы – парные, состоящие из двух требований). Введем параметр, характеризующий «смешанность» потока. Пусть Р – вероятность того, что поступившая заявка – одинарная, соответственно 1 – Р – вероятность того, что поступившая заявка – групповая. Таким образом, при Р = 0 поток является групповым (парным), при Р = 1 поток является ординарным.

При поступлении одинарной заявки в систему с каналами равной производительности она занимает любой из свободных каналов, если интенсивности приборов различны – она обслуживается наиболее «быстрым» свободным устройством (как показано в [5], данная схема управления потоком является наиболее эффективной для систем с неэквивалентными каналами). При поступлении в СМО парной заявки ее требования одновременно занимают два прибора (при этом, если производительности каналов различны, одно из требований по завершении обслуживания может покинуть систему раньше другого), если один или два канала системы заняты – парная заявка получает отказ в обслуживании и покидает систему.

В рамках работы проведена серия имитационных экспериментов на базе программного комплекса AnyLogic [8, 9]. Модель двухканальной системы, функционирующей в условиях смешанных потоков, представлена на рисунке. Она состоит из ряда стандартных блоков для создания (sourse), задержки (delay, delay1), уничтожения (sink – sink4) и управления потоками заявок, функции и нескольких переменных. Стоит отметить, что методы имитационного моделирования по определению предполагают некоторую погрешность в результатах и требуют проверки адекватности моделей, при этом позволяют с достаточной степенью точности исследовать СМО (как показано в [10], относительная погрешность имитационных моделей систем с неэквивалентными каналами может составлять около 1 %).

В качестве показателей эффективности рассматриваются р0 – вероятность того, что система свободна, и ротк – вероятность отказа в обслуживании.

Параметры исследуемых моделей представлены в табл. 1. В рамках серии имитационных экспериментов проведен сравнительный анализ показателей эффективности классической системы, обладающей каналами одинаковой производительности μ1 = μ2 = 5 (строка «СМО-0»), и систем с неэквивалентными каналами при различных соотношениях интенсивностей приборов от μ1 = 4,5, μ2 = 5,5 (строка «СМО-1») до μ1 = 1, μ2 = 9 (строка «СМО-8»). Суммарная производительность каналов во всех рассматриваемых системах равна μ1 + μ2 = 10.

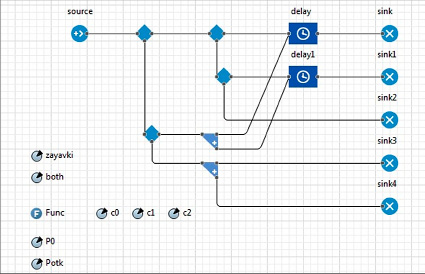
Имитационная модель СМО

Таблица 1

Параметры исследуемых моделей

Результаты исследования и их обсуждение

Рассмотрим результаты сравнительного анализа функциональных характеристик системы массового обслуживания при Р = 0 (поток парных заявок).

В табл. 2 представлена разница в показателях эффективности р02 – р01, где р02 – вероятность того, что система с неэквивалентными каналами свободна, р01 – вероятность того, что система с каналами одинаковой производительности свободна. Таким образом, отрицательные значения ячеек в данной таблице указывают на то, что система с неэквивалентными каналами в данных условиях менее эффективна, чем классическая СМО. Очевидно, что при групповом потоке разница в показателях ротк будет та же.

По результатам анализа таблицы представляется возможным сформулировать вывод о том, что в условиях группового потока СМО с неэквивалентными каналами являются менее эффективными, чем классические системы с приборами одинаковой производительности.

Таблица 2

Разница в показателях р0 при групповом потоке (Р = 0)

Таблица 3

Разница в показателях р0 при смешанном потоке (P = 0,5)

Увеличение диспропорции в интенсивностях обслуживающих устройств приводит к значительному ухудшению показателей эффективности. К примеру, рассмотрим результаты при λ = 5. При незначительной диспропорции в интенсивностях каналов разница в показателях равна р02 – р01 = –0,003 (см. столбец «СМО-1»), что сравнимо с погрешностью методов имитационного моделирования. В то же время при увеличении диспропорции в интенсивностях обслуживающих устройств до μ1 = 1, μ2 = 9 разница в показателях составляет уже р02 – р01 = –0,23 (см. столбец «СМО-8»). Такое поведение системы наблюдается на всем диапазоне нагрузки от λ = 1 до λ = 15. Значительное ухудшение показателей эффективности при увеличении диспропорции каналов связано с тем, что время обслуживания групповой заявки становится равным времени обслуживания требования наиболее «медленным» прибором. Таким образом, при групповых потоках использование систем с неэквивалентными каналами представляется нецелесообразным.

Рассмотрим СМО, функционирующие в условиях смешанных потоков. По результатам экспериментов с моделями двухканальных систем, представленных в табл. 1, установлено, что положительные значения р02 – р01 (значения, при которых система с неэквивалентными каналами может быть эффективнее классической системы) наиболее характерно появляются при Р ≥ 0,5, то есть когда вероятность поступления в систему одинарной заявки больше, чем вероятность поступления парной заявки. С учетом этого в рамках настоящей статьи ограничимся рассмотрением материалов при Р ≥ 0,5.

В табл. 3 представлены результаты экспериментов при смешанном потоке, характеризующемся равной вероятностью поступления одинарных и парных заявок P = 0,5.

Материалы таблицы демонстрируют, что при P = 0,5 система с каналами различной производительности в целом проявляет себя хуже классической СМО, однако при небольшой диспропорции в интенсивностях обслуживающих устройств (см. столбцы «СМО-1» и «СМО-2») имеются некоторые положительные области, в которых система с неэквивалентными каналами может быть эффективнее системы с одинаковыми приборами.

В табл. 4 представлены результаты имитационных экспериментов при P = 0,7.

По результатам анализа материалов табл. 4 видно, что при P = 0,7 области эффективности системы с неэквивалентными каналами выражены более характерно. К примеру, при λ = 3, μ1 = 4, μ2 = 6 (см. столбец «СМО-2») система с каналами различной производительности по показателю р0 на 0,016 превышает аналогичный показатель классической СМО. Несмотря на кажущуюся незначительность такой разницы, для систем, к примеру, обрабатывающих большие данные, она может дать ощутимое преимущество.

В табл. 5 представлены области эффективности при P = 0,9.

Значительную часть входного потока в данном случае составляют одинарные заявки. Видно, что при P = 0,9 области эффективности систем с неэквивалентными каналами являются значительно более характерными, чем в ранее рассмотренных примерах. Так, при λ = 1 разница в показателях р02 – р01 достигает 0,02.

Рассмотрим результаты имитационных экспериментов при P = 1, представленные в табл. 6. В данном случае поток является ординарным. По материалам таблицы видно, что при ординарном потоке области эффективности СМО с каналами различной производительности значительно расширились. Также заметим, что представленные области в целом совпадают с результатами, ранее полученными в [6] на примере трех- и четырехканальных СМО, функционирующих при пуассоновских потоках.

Стоит отметить, что в условиях смешанного потока системы с неэквивалентными каналами могут быть эффективнее классических СМО также по показателю ротк. Для параметров систем, представленных в табл. 1, разница в значениях ротк1 – ротк2 была не столь существенна, как в ранее рассмотренных примерах по показателю р0, и в некоторых моделях достигала 0,012. С учетом этого в рамках настоящей работы данные результаты мы приводить не будем, ограничившись рассмотренными областями эффективности по р0.

Таблица 4

Разница в показателях р0 при смешанном потоке (P = 0,7)

Таблица 5

Разница в показателях р0 при смешанном потоке (P = 0,9)

Таблица 6

Разница в показателях р0 при ординарном потоке (P = 1)

Таким образом, анализируя результаты имитационных экспериментов, представленные в табл. 2–6, видится возможным сформулировать вывод о существовании областей параметров, при которых системы с неэквивалентными каналами могут быть эффективнее систем с приборами одинаковой интенсивности в условиях смешанного потока. Данные области эффективности в значительной степени зависят от характера «смешанности» потока и преимущественно проявляются в условиях более высокой вероятности поступления одинарных заявок, чем групповых. С учетом продемонстрированных результатов также стоит отметить, что изучение систем такого типа представляется достаточно перспективным направлением исследований по теории массового обслуживания.

Выводы

1. В условиях группового потока системы массового обслуживания с каналами различной производительности являются менее эффективными, чем классические системы с приборами одинаковой интенсивности обслуживания.

2. В условиях группового потока увеличение диспропорции в интенсивностях каналов приводит к значительному ухудшению показателей эффективности системы. Это связано с тем, что время обслуживания групповой заявки становится равным времени обслуживания одного из требований наиболее «медленным» прибором.

3. Существуют области параметров (соотношение интенсивностей каналов, нагрузка на систему), при которых системы с неэквивалентными каналами могут быть эффективнее систем с приборами одинаковой производительности в условиях смешанных потоков.

4. Области эффективности систем с каналами различной производительности преимущественно проявляются при смешанном потоке, характеризующемся более высокой вероятностью поступления одинарных заявок, чем групповых. То есть чем более смешанный поток приближается к ординарному, тем данные области проявляются наиболее выраженно.

5. По аналогии с системами, функционирующими в условиях пуассоновских потоков, области эффективности систем с каналами различной производительности при смешанных потоках связаны с незначительной нагрузкой на систему и небольшой диспропорцией в интенсивностях каналов.