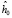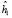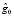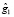Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Для повышения эффективности передачи информации в низкоорбитальном спутниковом интернете (НСИ) было предложено использовать системы OFDM [1]. С целью увеличения скорости передачи информации в системах, поддерживающих технологию OFDM, в работах [2, 3] было предложено использовать вместо быстрых преобразований Фурье целочисленные дискретные вейвлет-преобразования. Компактность данных преобразований позволяет увеличить скорость ортогональных преобразований сигналов. Для дальнейшего повышения скорости обработки сигналов было предложено реализовать в ЦДВП в модулярных кодах классов вычетов (МККВ) [4, 5]. Данная цель достигалась за счет параллельных вычислений, которые производились по основаниям кода. Однако МККВ можно использовать и для повышения отказоустойчивости вычислительных устройств. Для этого, во-первых, расширяется набор оснований кода за счет введения дополнительных контрольных модулей. Во-вторых, необходимо разработать алгоритм проверки процесса вычислений ЦДВП в МККВ с целью выявления ошибок, возникающих из-за сбоев или отказов. Очевидно, что интеграция методов вычисления ЦДВП и принципов построения корректирующих модулярных кодов класса вычетов требует разработки математической модели отказоустойчивой системы OFDM, способной осуществлять обработку сигналов в условиях сбоев и отказов, возникающих в процессе функционирования. Поэтому разработка такой математической модели отказоустойчивой системы OFDM является актуальной задачей.

Материалы и методы исследования

1.1. Теория построения избыточных кодов МККВ

Интеграция параллельных арифметических кодов и методов вычислений ЦДВП позволила повысить скорость ортогональных преобразований сигналов за счет ускорения выполнения арифметических операций, которые используются в дискретных вейвлет-преобразованиях. Чтобы распараллелить вычисления, необходимо найти взаимно-простые числа 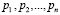, для которых выполняется неравенство 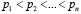. Если их перемножить, то получаем диапазон разрешенных кодовых комбинаций (КК) [6, с. 4]:

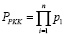. (1)

В этом случае разрешенную КК целого числа А можно представить как

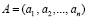, (2)

где А < РРКК; ai ≡ Amod pi , i = 1,2,…,n.

В МККВ параллельно выполняется сложение, вычитание и умножение [7, с. 12]

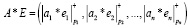,(3)

где * – модульные операции МККВ; E < РРКК; ei ≡ Emod pi , i = 1,2,…,n.

Анализ (3) показывает, что данные модульные операции выполняются с соответствующими остатками по всем основаниям кода одновременно. При этом между основаниями МККВ нет связи, то есть остатки друг на друга не влияют. Именно это используется при построении корректирующих МККВ. При этом данные коды имеют еще одно преимущество [8, с. 254]. Если расширить количество оснований для введения избыточности в КК, то принципы выполнения модульных операций для контрольных остатков не изменятся. Таким образом, контрольные остатки являются равноправными с информационными остатками, так определяются только модульными операциями. В этом заключено коренное отличие МККВ от других корректирующих кодов, используемых для повышения помехоустойчивости систем передачи.

1.2. Разработка метода поиска ошибочных остатков в МККВ

Для МККВ однократная ошибка представляет собой искажение одного остатка КК. Чтобы избыточный МККВ смог исправить такую ошибку, необходимо ввести контрольные основания 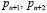. Они выбираются из условия

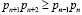. (4)

Из-за введения оснований, во-первых, увеличение размера кодовой комбинации:

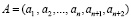. (5)

Во-вторых, диапазон РРКК расширяется до полного, содержащего все возможные КК:

Pполн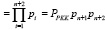. (6)

В избыточном МККВ разрешенными будут только те комбинации, для которых

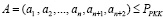. (7)

Однако проверить условие (7), не выполнив перевод КК в позиционную систему счисления (ПСС), нельзя. Решить данную проблему можно, если использовать равнозначность информационных и контрольных остатков в МККВ. В этом случае возникает возможность вычисления значений контрольных остатков 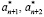, используя информационные остатки. Если в процессе вычислений ошибок из-за сбоев или отказов не было, то справедливо равенство 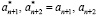. В этом случае имеет место равенство

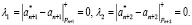(8)

Если ошибки имели место, то справедливость равенства (9) нарушается.

Очевидно, что эффективность данного подхода к коррекции ошибки во многом определяется алгоритмом, позволяющим вычислять контрольные остатки. В работе [8, с. 68–70] представлен алгоритм расширения системы оснований, то есть вычисления остатка ak+1 по заданному входному вектору A = (a1, a2, ..., an ). Данный алгоритм построен на основе Китайской теоремы об остатках (КТО), в которой, используя n – 1 информационный остаток, выполняется перевод в ПСС:

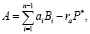(9)

где 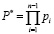; Bi – ортогональные базисы; 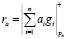– ранг числа A; ;

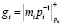mi – вес ортогонального базиса; i = 1,2,…,n–1, .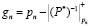

Подставив выражение для вычисления ранга в равенство (9), получаем, что

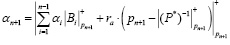. (10)

Недостатком этого алгоритма является сокращение числа разрешенных комбинаций в pn раз, так, при вычислениях используется n – 1 информационный остаток. Устранить этот недостаток позволяет разработанный метод вычисления контрольного остатка. Пусть задан код МККВ, состоящий из n информационных и одного контрольного основания pn+1. Если КК избыточного МККВ разрешенная, то номер диапазона, в который КК подает, равен

H = [ A / PPKK ] = 0. (11)

Воспользуемся КТО для n +1 оснований МККВ и подставим (9) в выражение (11). При этом учитываем, что номера диапазонов Н изменяются от 0. Значит, операцию нахождения целой частного Н в (11) можно заменить операцией по модулю pn+1. Тогда

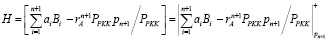. (12)

Исходя из условия взаимной простоты оснований pi, i = 1,2,…,n + 1, имеем

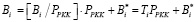, (13)

где Bi* – ортогональный базис для МККВ, содержащего кортеж оснований .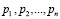

Подставим выражение (13) в равенство (12). Получаем

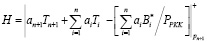. (14)

Если комбинация МККВ не содержит ошибку, то Н = 0. Тогда справедливо

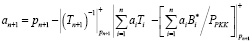. (15)

1.3. Математическая модель отказоустойчивой системы OFDM, использующей избыточный МККВ

Математическая модель отказоустойчивой системы OFDM, использующей избыточный МККВ, включает в себя следующие этапы обработки данных.

1. На первом этапе производится перевод данных из последовательного вида в параллельный. Сначала потоковые данные разбиваются на блоки 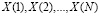, состоящие из D разрядов, где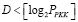. Затем каждый такой блок поступает на вход прямого преобразователя ПСС-МККВ, поддерживающего 2M-арный алгоритм вычислений, где он делится на блоки по С = 2M бит каждый. Блоки имеют следующий вид:

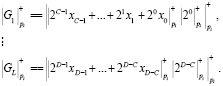(16)

Чтобы получить остатки, преобразователь вычисляет, где i = 1,2,…,n + 2

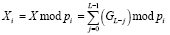. (17)

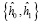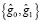2. На втором этапе в отказоустойчивой системе OFDM производится вычисление обратного модифицированного вейвлет-преобразования Хаара в МККВ [5]. Набор отсчетов X(j) – это кортеж, включающий {ai} – аппроксимирующие и {dj} детализирующие коэффициенты ЦДВП Хаара, которые представлены в МККВ. Для выполнения обратного преобразования используются и – коэффициенты НЧ и ВЧ фильтров Хаара. Математически данное обратное преобразование записывается выражением для

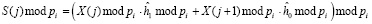, (18)

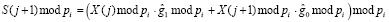, (19)

где 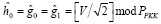; ; 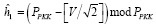V = 2W – коэффициент масштабирования; ; ; .

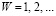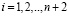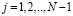3. Представленные в избыточном МККВ вычисленные временные отсчеты 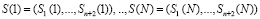необходимо перевести в ПСС. Для этого используется обратный кодопреобразователь, реализующий КТО [7, с. 81]. Для этого надо сначала получить ортогональные базисы МККВ согласно

Вi = Pimi = mi Pполн / pi, (20)

где 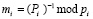– вес ортогонального базиса; .

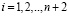Тогда согласно КТО обратный перевод МККВ-ПСС реализуется

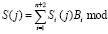Pполн. (21)

Одновременно с этим преобразованием выполняется разработанный метод поиска и исправления ошибки. Для этого сначала вычисляются контрольные вычеты:

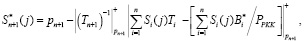(22)

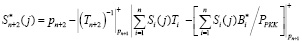. (23)

Затем выполняется вычисление невязки:

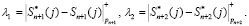(24)

Если λ1 = λ2 = 0, то в процессе ортогональной обработки сигналов сбоев и отказов не было. Пусть в процессе выполнения обратного ЦДВП Хаара в i-м остатке произошла ошибка. Тогда КК имеет вид

,

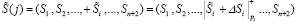где ΔSi = {1,2,…,Si – 1} – глубина ошибки. В этом случае имеем .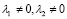

Затем происходит коррекция ошибки

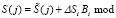Pполн. (25)

Исправленные отсчеты 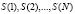поступают на вход АЦП, где преобразуются в аналоговый сигнал, который подается на модулятор, а затем в канал связи.

На приемной стороне аналоговый сигнал с помощью ЦАП преобразуется в кортеж отсчеты 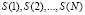, которые подаются на преобразователь ПСС-МККВ, с выхода которого снимаются КК МККВ .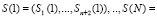

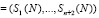Далее выполняется прямое ЦДВП Хаара в МККВ, что позволяет получить значение коэффициентов {ai} и {dj} в следующем виде: КК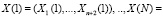 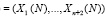. Полученные комбинации поступают на обратный кодопреобразователь МККВ-ПСС, который на основе КТО получает блоки данных длиной D разрядов, используя выражение (21). Одновременно с этим выполняется метод поиска и исправления ошибки согласно (14) и (15). Если λ1 = λ2 = 0, то в процессе ортогональной обработки сигналов сбоев и отказов не было. Если 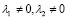, то производится коррекция ошибки искаженного отсчета 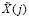согласно (25).

Результаты исследования и их обсуждение

Пусть имеем основания р1 = 63, р2 = 64, р3 = 65. Тогда РРКК = 262080, что позволяет использовать 9-разрядные входные данные и коэффициенты Хаара. В качестве контрольных выбрали р4 = 67, р5 = 71. Тогда Рполн = 1246714560. Пусть, коэффициент масштабирования V = 28. Пусть на вход передатчика поступили два отсчета Х1 = 221 и Х2 = 198, которые поступили на вход преобразователя ПСС-МККВ. Кодовые комбинации МККВ входных отсчетов Х1 и Х2, коэффициентов Хаара, отсчетов сигналов S1 и S2 показаны в таблице.

При вычислении S1 и S2 были использованы выражения (18) и (19). Проведем проверку КК 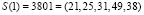. Вычислим ортогональные базисы для оснований р1 = 63, р2 = 64, р3 = 65, р4 = 67. Представим их, как показано выражением (13). Тогда

,

;

;

.

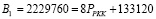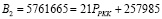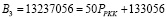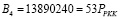Находим 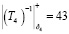. Подставляем в выражение (22). Получаем

.

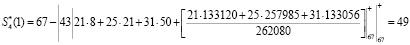Аналогичным образом получили второй контрольный остаток 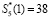. Подставляем в выражение (24) и получаем λ1 = λ2 = 0. Значит, ошибки в кодовой комбинации нет. Пусть ошибка произошла в первом остатке, тогда КК имеет вид 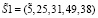. Глубина ошибки равна ΔS1 = 47. Используя выражения (22) и (23), получаем 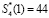и 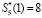. Так как λ1 = 62, λ2 = 30, то согласно (25) происходит исправление ошибки:

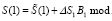Pполн .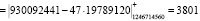

Вычисление первых двух отсчетов сигналов ЦДВП Хаара в МККВ

Заключение

В статье представлена математическая модель отказоустойчивой системы OFDM, использующей ЦДВП Хаара в МККВ. Разработан метод коррекции ошибок на основе расширений системы оснований. Разработанный метод позволяет провести вычисление контрольных остатков, на основе кортежа информационных, имея больший диапазон разрешенных кодовых комбинаций по сравнению с [8, с. 68–70]. Рассмотрен процесс вычисления отсчетов сигнала с помощью обратного ЦДВП Хаара, а также процесс поиска и коррекции ошибок с использованием трех информационных р1 = 63, р2 = 64, р3 = 65 и контрольных оснований р4 = 67, р5 = 71. Применение разработанного метода позволило увеличить РРКК в 65 раз по сравнению с алгоритмом [8, с. 68–70].