Системы искусственного интеллекта активно внедряются в повседневную человеческую деятельность. Немаловажное влияние они оказывают и на контроль качества. Объединяя искусственные нейронные сети или экспертные системы с программами автоматизированных систем управления технологическими процессами, возможно получить более точные результаты оценки и, как следствие, более продуктивные и результативные управляющие воздействия на исполняющие устройства. Однако пока мало проработан контроль качества самой автоматизированной системы. Для этих целей также может быть применена экспертная система. Она может предназначаться для превентивного расчета вероятности отказа на основе индикации его предвестников. Разработка и реализация экспертных систем обнаружения предвестников отказов является актуальной задачей, основная трудность которой состоит в формировании математической модели и структуры преобразования ее данных.
Цель исследования заключается в разработке математической модели экспертной системы обнаружения предвестников отказов на основе показателей безотказности и ремонтопригодности.
Материалы и методы исследования
Для достижения цели исследования возможно применение основных теорий и принципов построения экспертных систем, моделей нечеткого вывода и набора показателей (в данном случае показателей надежности систем).
Экспертные системы, наряду с искусственными нейронными сетями, являются одним из видов систем искусственного интеллекта и предполагают наличие моделей и знаний об объекте управления или предметной области.
Основной моделью в таких системах является модель нечеткого вывода, которая необходима для преобразования значений входных параметров в значения выходных, на основе функций принадлежности и набора нечетких правил. Можно выделить несколько моделей нечеткого вывода:
− модель нечеткого вывода Мамдани [1]. В основе данной модели заложено применение операции минимизации для получения усеченной функции принадлежности;
− модель нечеткого вывода Ларсена [2]. Схожа с моделью Мамдани. При расчете усеченной функции применяется алгебраическое произведение;
− модель нечеткого вывода Тсукамото [3]. Применяется для параметров, функция принадлежности которых монотонна;
− модель нечеткого вывода Сугэно [4]. Предполагает линейные функции принадлежности.
Каждая из моделей содержит набор схожих этапов преобразования данных:
1. Этап фаззификации входных данных. Разделение множества возможных значений входных и выходных параметров экспертной системы на диапазоны отнесения в соответствии с функциями принадлежности и заложенными нечеткими правилами.
2. Этап логического вывода. Расчет промежуточных значений, необходимых для формирования вывода.
3. Этап дефаззификации. Преобразование нечеткого значения вида усеченной функции принадлежности в итоговое значение выходного параметра.
Знания в экспертных системах структурируются в базы знаний и содержат формализованную информацию:
− о типах функций принадлежности (треугольных, трапециевидных, Гауссовых, сигмоидальных, Z-образных, S-образных, П-образных и т.д.). Влияют на степень отнесения значения параметра к определенному терму функции, который в последующем учитывается в нечетком правиле;
− о параметрах функций принадлежности, определяющих положение и форму выбранных функций принадлежности. Для разных типов функций принадлежности необходим разный набор параметров, описывающих начальные и конечные точки диапазонов отнесения;
− о наборах нечетких правил, отображающих взаимосвязи выходных и входных параметров экспертной системы. Нечеткие правила могут быть заданы в явном виде (строкой) либо в виде созависимых термов параметров. Выбор зависит от программных возможностей и функций экспертной системы и базы знаний;
− о рекомендациях по заданным условиям, которые по итогу работы системы выводятся оператору с целью упрощения формирования решений по полученным результатам. Рекомендации связаны с определенными комбинациями значений параметров (или их отнесения к термам) либо с итоговым значением системы;
− об объяснениях получаемых результатов, выводимых оператору по мере работы экспертной системы и содержащих дополнительную информацию по процессу преобразования данных. Объяснения предполагаются экспертными системами и полностью зависят от применяемых моделей.
Как модели, так и знания в экспертных системах основаны на применяемых в ней параметрах. Для построения экспертных систем обнаружения предвестников отказов возможно применение различных показателей в качестве параметров. Одним из вариантов является использование показателей надежности, которые могут быть подразделены на две группы [5]:показатели безотказности (t – случайная величина длительности времени до первого отказа или между средними отказами, p(t) – плотность распределения вероятности отказа, N0 – число образцов изделий в начале наблюдения, N1 – число отказавших изделий за время t, N(t) – число элементов, оставшихся исправными в конце рассматриваемого интервала времени t, γ – число изделий, не достигающих с заданной вероятностью предельного состояния, Тсл – срок службы, f(t) – плотность распределения случайной величины t, Тсp – средняя наработка до первого отказа или среднее время безотказной работы, λ1(t) – параметр потока отказов для восстанавливаемых изделий, λ(t) – интенсивность отказов, Тс.сp – статистически рассчитанная средняя наработка до первого отказа или среднее время безотказной работы, Рс(t) – статистически рассчитанная вероятность безотказной работы за время t (функция надежности), ω(t) – средняя частота отказов, Р(tγ) – гамма-процентный ресурс); показатели ремонтопригодности (ti – суммарная наработка i-го изделия в заданном интервале эксплуатации, tвi – суммарное время восстановления i-го изделия за этот же период эксплуатации, n – общее число отказов, Р(t0,t1) – вероятность безотказной работы изделия в интервале времени t0,t1, Wonj – оперативная трудоемкость выполнения технического обслуживания i-го вида, рассчитываемая в человеко-часах, nj – количество внеплановых текущих ремонтов (отказов) j-го вида за расчетный период, tonj – оперативное время, характеризующее затраты времени исполнителей на выполнение основных и вспомогательных операций при ликвидации отказа, kг – коэффициент готовности, Тс.в – статистически рассчитанное среднее время восстановления, Сэ – стоимость эксплуатации до капитального ремонта, Со – стоимость оборудования, kог – коэффициент оперативной готовности, μ(t) – интенсивность восстановления, Wвнj – средняя оперативная трудоемкость внепланового текущего ремонта, Твнj – средняя оперативная продолжительность внепланового текущего ремонта, kсэ – коэффициент стоимости эксплуатации).
Экспертная система предполагает преобразование данных в несколько этапов, а экспертная система обнаружения предвестников отказов помимо этого учитывает данные за несколько периодов, в целях повышения точности выходного параметра, которым является вероятность возникновения отказа и набор рекомендаций по улучшению объекта управления. Основными этапами преобразования являются:
1. Получение и проверка входных данных. Значения входных параметров системы могут быть получены от оператора системы либо от соответствующих устройств автоматизированной системы управления, в которой применяется экспертная система обнаружения предвестников отказов. В связи с этим возникает необходимость в формализации получаемой информации.
2. Преобразование входных параметров в используемые данные. Применение входных данных в качестве параметров последующих моделей экспертной системы не всегда является результативным решением. Следует предполагать возможность преобразования входов экспертной системы в комбинированные параметры, точнее описывающие характеристики исследуемого объекта и его неопределенности.
3. Обработка данных в соответствии с выбранной моделью нечеткого вывода. Такая модель определяет последовательность и логику преобразования значений входных параметров в значения выходных параметров. Могут быть применены различные модели. При их выборе необходимо ориентироваться на тип экспертной системы, к примеру MISO-системы (multiple-input/single-output), предполагающие получения единичного значения по нескольким исходным.
4. Формирование и преобразование набора объяснений и рекомендаций. Набор объяснений зависит от экспертных знаний, заложенных в базу знаний, а также применяемых логических преобразований. При желании разработчика добавить дополнительные функции уместным является расширение спектра предоставляемых оператору объяснений и рекомендаций. Помимо рекомендаций, ориентированных на объект исследования и управления им, возможно приведение аналогий и примеров заполнения полей экспертной системы.
5. Формирование и преобразование выходного значения системы (вероятность возникновения отказа). Данные функции экспертной системы ориентированы на ее основной выход и должны быть реализованы и проверены в первую очередь. Возможно применение формализации вывода с целью последующего предоставления информации в нужном виде.
6. Вывод информации оператору системы.
На основе основных формул преобразования показателей надежности, а также основных этапов преобразования данных в экспертной системе обнаружения предвестников отказов, возможно построение схемы показа и преобразования данных, представленной на рисунке. На схеме цифрами обозначены этапы преобразования. Первый и второй этапы выполняются несколько раз в зависимости от количества выбранных периодов сбора данных и отслеживания характеристик управляемого объекта.
Такая схема преобразования может быть использована для анализа любого технического объекта, к которому возможно применение показателей надежности. Учет разных свойств и особенностей таких объектов и связанных с ними технологических процессов достигается путем выбора соответствующих параметров функций принадлежности в модели нечеткого вывода, а также границами термов этих функций. Параметры могут быть получены экспертным путем в ходе опроса и сбора знаний предметной области, либо же на основе статистических данных. Однако во втором случае, при наличии таких данных, возможно применение нейронных сетей, что, возможно, даст более точный по сравнению с экспертными методами результат.
На вход потока данных, представленного схемой, подаются значения параметров t, p(t), N0, N1, N(t), γ, Тсл, ti, tвi, n, Р(t0,t1), Wonj, nj, tonj, Сэ, Сo, описание которых было представлено ранее. Структура связей обусловлена математическими формулами получения соответствующих параметров из входных и промежуточных значений (ГОСТ Р 27.010-2019).
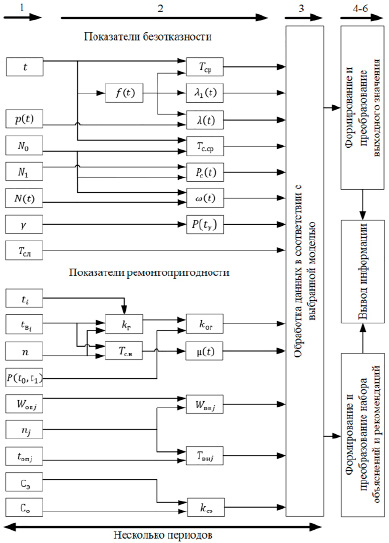
Схема потока и преобразования данных экспертной системы обнаружения предвестников отказов на основе показателей надежности
На основе представленной выше информации возможна разработка математической модели экспертной системы обнаружения предвестников отказов на основе показателей надежности, описание которых было представлено ранее. Она предполагает получение значения вероятности возможного отказа исследуемого объекты и набора рекомендаций по его улучшению. При применении для этих целей показателей безотказности и ремонтопригодности, математическая модель приобретает следующий вид:
f (t, p(t), N0, N1, N(t), γ, Тсл, ti, tвi, n, Р(t0,t1), Wonj, nj, tonj, Сэ, Сo) = < p, R >,
где f – функция, основанная на нечеткой логике; p – вероятность возникновения отказа; R – множество рекомендаций по отказам.
Однако для получения более точной оценки вероятности отказа и более релевантных текущей ситуации рекомендаций следует учитывать тренд развития показателей и характеристик исследуемого объекта. Учитывая значения нескольких прошлых периодов, математическая модель может быть преобразована в следующий вид:
f (< t, p(t), N0, N1, N(t), γ, Тсл, ti, tвi, n, Р(t0,t1), Wonj, nj, tonj, Сэ, Сo >T),…,
< t, p(t), N0, N1, N(t), γ, Тсл, ti, tвi, n, Р(t0,t1), Wonj, nj, tonj, Сэ, Сo >–kT) = < p, R >,
где T – период сбора значений параметров; k – индекс периода.
Входные параметры не являются конечными показателями безотказности и ремонтопригодности, и, как следствие, необходимо рассматривать комплексные показатели. Их применение изменяет и математическую модель соответствующей экспертной системы обнаружения предвестников отказов:
f (< Тср, λ1(t), λ(t), Тс.ср, Рс(t), ω(t), Р(tγ), Тсл, kог, μ(t), Wнвj, Тнвj, kсэ >T),…,
< Тср, λ1(t), λ(t), Тс.ср, Рс(t), ω(t), Р(tγ), Тсл, kог, μ(t), Wнвj, Тнвj, kсэ >–kT) = < p, R >.
Учитывая, что в основе экспертной системы заложена определенная модель нечеткого вывода, возможно уточнение общей математической модели экспертной системы обнаружения предвестников отказов:
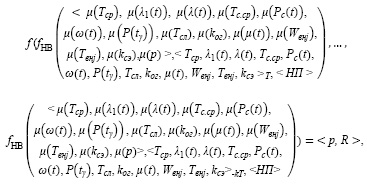
где fHB – функция, основанная на модели нечеткого вывода; μ – функция принадлежности; <НП> – набор нечетких правил.
Таким образом, полученная математическая модель в полной мере отражает преобразование данных в экспертной системе обнаружения предвестников отказов на основе показателей надежности, а также содержит информацию о входных и выходных параметрах системы и может быть использована при построении соответствующих экспертных систем.
Результаты исследования и их обсуждение
В ходе исследования были решены следующие задачи:
1. Проанализированы основные модели нечеткого вывода на предмет этапов преобразования данных. Такие модели являются общепринятыми, а модели Мамдани и Ларсена – применимыми для обнаружения предвестников отказов.
2. Классифицированы знания в экспертных системах обнаружения предвестников отказов. Каждый из классов может быть реализован по-разному в зависимости от принятого программистом решения, в согласовании с инженером по знаниям.
3. Выбраны и проанализированы показатели надежности, которые могут быть использованы в качестве параметров экспертной системы обнаружения предвестников отказов. Для задач соответствующей экспертной системы возможно применение и других показателей (индикаторных показателей процесса, показателей теории очередей и т.д.). Показатели надежности в большей степени ориентированы на технические характеристики элементов исследуемого объекта, что может усложнить процесс идентификации рисков, связанных с обрабатываемой продукцией.
4. Сформирована схема потока и преобразования данных экспертной системы обнаружения предвестников отказов на основе показателей надежности. Такая схема может быть использована при разработке алгоритмов программной реализации экспертной системы. Анализируя данную схему, можно заметить большое число входных данных, что может привести к усложнению процедуры применения экспертной системы со стороны оператора, вызванному необходимостью получения значений этих данных (из различных источников).
5. Разработана математическая модель экспертной системы обнаружения предвестников отказов на основе показателей надежности. На ее основе возможно построение модели взаимосвязи модулей, архитектуры соответствующей экспертной системы и последующая ее программная реализация.
Заключение
Набирающие популярность системы искусственного интеллекта могут быть в полной мере применены и для задач контроля качества и выявления предвестников отказов исследуемых систем и/или рискованных событий технологического процесса. Рассмотренные в данной статье положения позволяют ускорить программную реализацию экспертных систем обнаружения предвестников отказов, основанных на показателях надежности, путем применения разработанных схемы потока и преобразования данных, а также математической модели.
Положения данной статьи могут быть перенесены с незначительными изменениями и на другие экспертные системы схожего направления. К возможным изменениям можно отнести применение других показателей (замена показателей надежности на другие) либо применение других моделей нечеткого вывода, ориентированных на специфические нечеткие правила и параметры модели.



