Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Динамика и особенности развития отечественной экономики, в том числе активность предпринимательского сектора экономики, являются актуальной проблемой и предметом исследования многих ученых. В более ранних научных публикациях авторов исследованы особенности развития и механизмы мотивации малого и среднего бизнеса [1, 2]. Дальнейшим развитием данного направления является настоящая публикация авторов в контексте исследования и оценки активности предпринимательского сектора отечественной экономики.

Целями исследования являются выявление показателей, которые могут быть приняты в качестве индикаторов активности предпринимательского сектора экономики, а также разработка ряда моделей для оценки их величины и динамики.

Материалы и методы исследования

Материалами исследования послужили официальные статистические данные, характеризующие развитие отечественной экономики за 2005–2022 годы. В качестве методов исследования использованы научные методы экономической теории, комплексного системного анализа, специальные методы вероятностно-статистического моделирования, методы анализа статистических данных в среде Рython и Excel.

Результаты исследования и их обсуждение

Одними из основных индикаторов реализации национальной цели обеспечения достойного труда населения и успешного развития предпринимательского сектора отечественной экономики, обозначенными в указе Президента Российской Федерации от 21.07.2020 № 474 «О национальных целях развития Российской Федерации на период до 2030 года», являются: темп роста валового внутреннего продукта, рост среднего уровня доходов населения, рост инвестиций в основной капитал, рост численности населения, занятого в предпринимательской сфере экономики [3].

Многофакторная модель оценки активности предпринимательского сектора экономики может быть записана в виде:

Y(А)t = f (KIt , NKIt) + εt , (1)

где Y(А)t – индикатор активности предпринимательского сектора экономики;

KIt – факторы, значение которых может подлежать количественному измерению;

NKIt – качественные факторы, значение которых в ряде случаев не подлежит количественному измерению;

εt – стохастическая составляющая, характеризующая ряд не учтенных в модели факторов и отражающая вероятностный характер процесса моделирования.

С учетом обозначенных ориентиров национальных целей развития экономики Российской Федерации оценки активности предпринимательского сектора в качестве результативного признака и факторов-регрессоров могут быть использованы показатели, которые наглядно представлены в таблице 1.

Необходимо отметить, что данные показатели выбраны по усмотрению исследователей и что одни и те же показатели в зависимости от целевой установки могут быть использованы в качестве результативного признака (например, темп роста инвестиций в основной капитал), а также в качестве фактора-регрессора (величина объема инвестиций в основной капитал при моделировании величины валового внутреннего продукта).

Осуществим рассмотрение одного из интегральных показателей, отражающего активность предпринимательского сектора российской экономики, – величины валового внутреннего продукта, созданного коллективным трудом занятого населения страны.

Построение математических моделей оценки активности предпринимательского сектора экономики осуществлено в среде Рython.

Таблица 1

Построение системы показателей многофакторной модели

Примечание: составлено авторами.

Для построения моделей были использованы: библиотеки работы с данными Pandas, DataFrame; библиотека работы со статистическими вычислениями (характеристиками) временных рядов NumPy; библиотеки matplotlib и seaborn, содержащие инструменты визуализации данных; библиотека Statsmodels, включающая инструменты построения моделей временных рядов; библиотека инструментов машинного обучения Scikit-learn.

Загрузка необходимых библиотек для анализа статистических данных осуществлена следующим образом:

!pip install pandas numpy matplotlib seaborn statsmodels scikit-learn

Для контроля ввода информации, соответствующей временным рядам анализируемых показателей, была осуществлена проверка корректности формата загруженных данных после изменения формата «Годы»:

# Column Non-Null Count Dtype

--- ------ -------------- -----

0 Годы 17 non-null datetime64[ns]

1 ВВП, млрд руб. 17 non-null float64

2 Доходы населения РФ, руб. 17 non-null float64

3 Инвестиции в осн кап., млн руб. 17 non-null float64

4 Численность занятых МСП*, млн чел. 17 non-null float64

5 Числ.занят.РФ, тыс. 17 non-null float64

6 Оброт МСП*, млрд руб. 17 non-null float64

7 V бюдж ас, млрд 17 non-null float64

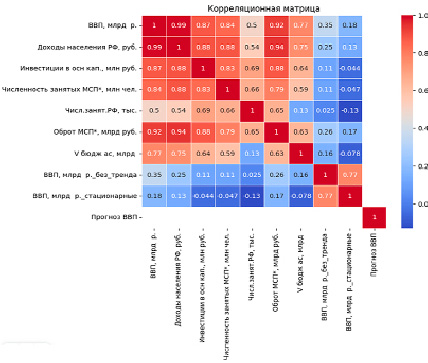
Рис. 1. Тепловая карта корреляционной зависимости показателей в Python Источник: получено авторами по [4, 5]

С целью выявления корреляционной зависимости показателей, характеризующих активность предпринимательского сектора экономики, осуществлен расчет характеристик корреляции в среде Python.

# Вычисление корреляций между показателями

correlation_matrix = df.corr()

# Визуализация корреляционной матрицы

import seaborn as sns

plt.figure(figsize=(8, 6))

sns.heatmap(correlation_matrix, annot=True, cmap=’coolwarm’, linewidths=0.5)

plt.title(‘Корреляционная матрица’)

plt.show()

Тепловая карта корреляционной зависимости исследуемых показателей в Python представлена на рисунке 1.

На основании полученных данных сделаны следующие выводы: ряд факторов-регрессоров, таких как численность занятого населения, объем инвестиций в основной капитал, объем бюджетных ассигнований (государственной поддержки) на развитие предпринимательского сектора экономики, оборот предприятий, имеют тесную положительную корреляционную связь с результативным признаком.

С целью повышения достоверности результатов математического моделирования была осуществлена проверка временных рядов показателей на стационарность, которая характеризует постоянство во времени таких статистических параметров признаков, как среднее значение и дисперсия. Фрагмент программирования проверки стационарности результативного признака:

result = adfuller(df[‘ВВП, млрд р.’])

print(‘Статистика ADF:’)

print(‘p-значимость:’)

print(‘Критические области:’)

for key, value in result[4].items():

print(‘\t%s: %.3f’ % (key, value))

Статистика ADF: 0.863422

p-значимость: 0.992594

Критические области:

1%: -3.924

5%: -3.068

10%: -2.674

Для построения модели множественной регрессии в среде Python было осуществлено задание результативного и факторных признаков:

#определим результативный признак

y = df[‘ВВП’]

#факторные признаки

x = df[[‘Доходы населения РФ’,’Инвестиции в основной капитал’,’Численность занятых МСП’,’Численность занятых РФ’,’Оброт МСП’, ‘V бюдж ас’]]

#добавим константу к переменным-предикторам

x = sm.add_constant(x)

После выявления корреляционной зависимости и оценки качества статистических данных построена многофакторная модель зависимости валового внутреннего продукта от ряда факторов регрессоров:

VVP (t) = 0,497 + 0,003 VND (t) + 0,512 VI (t) + + 0,393 ANE (t) + 0,501 VNZ(t) + + 0,993 VOB(t) + 0,918 VGP (t). (2)

Построенная регрессия обладает высоким качеством, характеризуемым коэффициентом детерминации R2=0,984, т.е. 98,4% вариации результативного признака обусловлено вариацией факторов-регрессоров, введенных в данную модель. Для дополнительной оценки качества построенной регрессии был осуществлен анализ графика остатков с использованием функции plot_regress_exog() из библиотеки statsmodels. Визуальный анализ графика свидетельствует о случайном разбросе значений остаточной компоненты относительно нулевого значения, что позволяет утверждать о выполнении свойства случайности. Далее с использованием критерия Дарбина–Ватсона проведена проверка свойства независимости, т.е. отсутствия автокорреляции в остатках регрессии:

from statsmodels.stats.stattools import durbin_watson

#perform Durbin-Watson test

durbin_watson(model.resid)

1.5261772785602952

Статистика теста, равная 1,5262, находится в диапазоне (1,5; 2,5), что позволяет утверждать об отсутствии автокорреляции в ряде остатков регрессии.

В дополнение к данной многофакторной регрессии, по усмотрению исследователей, построена выборочная регрессия от ряда факторов, введенных в рассмотрение:

VVP (t) = – 6953,1425 + 6,6806 VI (t) + + 93,6398 VGP (t) – 0,0611 VOB (t). (3)

При исследовании качества данной многофакторной модели было установлено, что модель имеет высокий показатель качества, характеризуемый коэффициентом детерминации, равным 0,98, и критерий Фишера, равный 411. Однако при проверке критерия Стьюдента выявлено, что ряд факторов не являются статистически значимыми, и для повышения достоверности прогнозирования по решению исследователей они из рассмотрения удалены. В рассмотрении оставлен фактор VI «объем инвестиций в основной капитал», имеющий наивысший коэффициент корреляции с результативным признаком и являющийся статистически значимым по критерию Стьюдента. В этом случае имеем однофакторную регрессионную модель:

VVP (t) = –6804,9321 + 6,1465 VI (t). (4)

Данная модель имеет следующие показатели качества: коэффициент детерминации, равный 0,9882; критерий Фишера, характеризующий статистическую значимость уравнения регрессии, равный 1257,3537; критерий Стьюдента, определяющий статистическую значимость факторного признака, – 35,4591. Анализ данных характеристик позволяет утверждать, что построенная модель может быть использована для разработки прогнозов [6, 7].

На рисунке 2 представлены графики динамики величины валового внутреннего продукта (в номинальных ценах).

Осуществляя визуальный анализ графика, можно утверждать, что динамика величины валового внутреннего продукта имеет устойчивую положительную тенденцию в интервале анализа 2005–2022 гг. (в номинальных ценах). По данному показателю с целью углубленного анализа построены линейный и полиномиальный тренды 2-го порядка.

Результаты трендового анализа представлены в таблице 2.

Анализируя результаты трендового анализа, характеризуемые уравнениями:

VVP (t) = 6997,9 t + 15775, (5)

VVP (t) = 159,85 t2 + 4120,6 t + 24887, (6)

можно утверждать, что линейный и полиномиальный тренды с высокой степенью достоверности аппроксимируют динамику величины валового внутреннего продукта, исчисленного в номинальных ценах, подтверждая устойчивый положительный тренд на протяжении длительного временного интервала 2005–2022 гг. Устойчивая положительная тенденция динамики валового внутреннего продукта может быть принята в качестве индикатора поступательного развития российской экономики и активности предпринимательского сектора экономики на протяжении длительного интервала времени.

В рамках реализации национального проекта по развитию предпринимательской деятельности одной из ключевых национальных целей российской экономики обозначено обеспечение темпа роста валового внутреннего продукта не ниже среднего мирового уровня. Для определения динамики темпа роста величины валового внутреннего продукта рассмотрим графики, представленные на рисунке 3.

Результаты трендового анализа динамики темпа роста ВВП представлены в таблице 3.

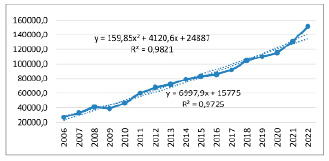
Рис. 2. Результаты трендового анализа ВВП (в номинальных ценах), млрд руб. Источник: составлено авторами

Таблица 2

Результаты трендового анализа величины валового внутреннего продукта РФ

Примечание: составлено авторами.

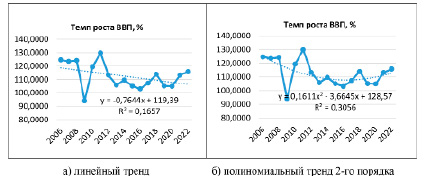
Рис. 3. Динамика темпов роста величины валового внутреннего продукта Источник: получено авторами

Таблица 3

Результаты трендового анализа динамики темпа роста ВВП Российской Федерации

Примечание: составлено авторами.

При анализе данные расчетов трендовые уравнения динамики темпов роста валового внутреннего продукта получают вид:

TVP (t) = – 0,7644 t + 119,39, (7)

TVP (t) = 0,1611 t2 – 3,6645 t + 128,57, (8)

что позволяет утверждать, что темп роста ВВП в интервале анализа 2005–2022 гг. имеет колебательную тенденцию с точками динамики, в большинстве случаев превышающими величину 100%, только в 2009 г. имеет место снижение темпа роста величины валового внутреннего продукта до уровня 94% по сравнению с предшествующим 2008 годом.

Заключение

Активность предпринимательского сектора отечественной экономики может быть оценена различными показателями, рассмотренными в данном исследовании. В качестве интегральных показателей, характеризующих в целом динамику развития отечественной экономики, по усмотрению исследователей были выбраны величина валового внутреннего продукта и темпы роста ВВП. Среднее значение темпов роста величины валового внутреннего продукта российской экономики за анализируемый период составило 119,5%, среднее значение цепного темпа прироста – 15,8%. Эти данные свидетельствуют о внутренних резервах российской экономики и, в целом, о положительной тенденции динамики величины валового внутреннего продукта сферы предпринимательства отечественной экономики.