Система советского образования отличалась фундаментальностью и научностью, однако реалии современной жизни требуют постоянного обновления знаний, трансформации системы образования. В реализации государственной программы Российской Федерации «Развитие образования» на 2018-2025 гг., федеральных государственных образовательных стандартах высшего образования последнего поколения без потери фундаментальности системы образования определено изменение её содержания усилением практико-ориентированной составляющей.
Практико-ориентированное обучение, предполагающее взаимодействие преподавателя, студента и работодателя, направлено на овладение студентами профессионально значимыми умениями и компетенциями. В его основе, по утверждению Ф.Г. Ялалова, лежит сочетание фундаментального образования и профессионально-прикладной подготовки для обеспечения связи содержания образования с реальными потребностями промышленности и социальной сферы [1]. Выпускник естественно-научных направлений вуза должен обладать не только глубокими знаниями по своей специальности, но и уметь применять различные, в том числе математические методы для разрешения профессиональных проблем, что отмечено в ФГОС ВО направлений 03.03.02 «Физика», 04.03.01 «Химия» и 06.03.01 «Биология». Разделы высшей математики студентами данных направлений изучаются с первого курса как базовая дисциплина. По мнению исследователей, при изучении конкретного материала математического курса на первый план должна быть выдвинута идея его связи с будущей профессией [2].
Цель исследования – разработка алгоритма конструирования профильных учебных материалов в обучении математике как способа организации активной продуктивной деятельности студентов для формирования умений применять математические знания в решении практических задач профессиональной направленности.
Материалы и методы исследования
Содержание образования всё более трансформируется из «знаниевой» в «деятельностные формы», вследствие чего меняются инструменты, формы и способы обучения [3]. Внедрение инструментальных средств математики как проявление рационализма в вузовском образовании опирается на избирательное применение математических методов и средств в решении проблем формирования профессионально значимых умений. В современном образовании возрастает значимость формирования умений через конструирование собственных образовательных продуктов. Исследователи внедряли процедуру конструирования в процессе подготовки экономистов, менеджеров, учителей математики и информатики и др. (И.А. Байгушева, М.В. Егупова, Е.Г. Плотникова и др. [4-6]).
В рамках исследования осуществлен анализ обобщенных трудовых функций профессиональных стандартов, соответствующих профессиональной деятельности выпускников по естественно-научным направлениям подготовки. Он позволил выделить формируемые в процессе обучения профессионально значимые умения: выполнение математических расчетов по направлениям подготовки, статистическая обработка полученных данных, графическое представление результатов, построение математических зависимостей в моделях изучаемых объектов и процессов и другие [7]. Состав математического инструментария, включающий математическое моделирование и задачный метод, был определен на основе компонентного анализа общепрофессиональных компетенций в ФГОС ВО перечисленных ранее естественно-научных направлений и направления 01.03.01 «Математика» [7].
Результаты исследования и их обсуждение
Процесс конструирования профильных учебных материалов осуществляется в активной познавательной деятельности на разных уровнях: содержательном, операциональном и оценочно-рефлексивном.
На содержательном уровне содержательный компонент учебных заданий в процессе конструирования обеспечивался включением естественно-научных знаний по профилю подготовки бакалавров, установлением междисциплинарных связей методов математики и содержанием профильных знаний [8]. Применение математического инструментария направлено на формирование профессионально значимых умений студентов- естественников, таких как установление причинно-следственных связей, моделирование, перекодирование информации и преобразование данных и др. В ходе исследования были определены критерии отбора содержания для конструирования практико-ориентированных заданий:
1. Соответствие содержания образовательным целям, образовательному стандарту и профессиональному стандарту по направлению подготовки студентов, интересам работодателей и личности студента.
2. Соответствие содержания практической значимости изучаемого материала для будущей профессиональной деятельности.
3. Соответствие содержания профильной ориентации студентов, их мотивации на овладение будущей профессией.
4. Соответствие содержания конструируемых практико-ориентированных заданий возможностям математического инструментария, возможностям графического отображения результатов конструирования и формирования умений представлять результаты экспериментальной и исследовательской деятельности студентов.
5. Соответствие объема содержания времени, отводимому для изучения данного учебного материала, за счет использования возможностей современных средств, приемов образовательных технологий, методов и форм обучения.
Таким образом, отбор содержания математических и профильных дисциплин осуществлялся на основе критериев общедидактической системы Ю.К. Бабанского, адаптированных под цели исследования [9].
На операциональном уровне конструирование профильных учебных материалов средствами математического инструментария потребовало анализа дидактических функций учебных заданий, определения этапов конструирования (алгоритма) профильных учебных материалов по направлениям подготовки средствами математического инструментария в комплексе с компьютерной поддержкой. С учетом дидактических функций учебных заданий и их классификации по таксономии Б. Блума полного усвоения знаний осуществлен отбор таких видов заданий, как:
− задачи с производственным содержанием, решение прямых и обратных задач (по технологии укрупнения дидактических единиц П.М. Эрдниева [10];
− составление системы взаимосвязанных задач, составление контекстных задач (А.А. Вербицкий [11]);
− ситуативные задачи, составленные с помощью конструктора Л.С. Илюшина [12].
На оценочно-рефлексивном уровне процесс конструирования профильных учебных материалов с применением дидактических приемов образовательных технологий (укрупнения дидактических единиц П.М. Эрдниева, контекстного обучения А.А. Вербицкого, конструктора задач Л.С. Илюшина) требует анализа и самоанализа результатов конструирования путем интерактивного обсуждения корректности задачной ситуации, фабулы задач, обсуждения формулировок и правильного построения текста. На этом уровне диагностика корректности конструирования учебных материалов, оценка и самооценка полученных результатов конструирования является сложной малоисследованной проблемой и требует отдельного исследования.
Методика конструирования профильных учебных материалов в обучении математике включает умения:
− анализировать задачную ситуацию, задаваемую математическим методом;
− осуществлять отбор профильного материала из профессиональной сферы направления подготовки;
− выявлять характер математической зависимости;
− формулировать условия для рационального пути решения;
− правильно осуществлять перенос задачной ситуации из профессиональной деятельности на символьный математический язык;
− осуществлять преобразования;
− определять фабулу задачи и выполнять решения;
− корректно формулировать составленную задачу с помощью конструктора задач;
− выполнять самоанализ построенной задачи.
Деятельность субъектов педагогического процесса на этапах конструирования учебных материалов
|
Субъект процесса обучения Уровень конструирования |
Преподаватель |
Студент |
|
Содержательный |
− определение специфики и содержания будущей профессиональной деятельности студентов; − координация усилий с преподавателями профильных дисциплин по разработке и корректировке ОПОП и фонда оценочных материалов |
− выбор типа ресурсов для осуществления поиска; − поиск производственной и профессионально значимой информации |
|
Операциональный |
− создание банка учебных заданий практико-ориентированных заданий и методических рекомендаций в СДО; − отбор приемов образовательных технологий |
− составление задач по аналогии с помощью приемов предложенных образовательных технологий; − конструирование учебных материалов |
|
Оценочно-рефлексивный |
диагностика корректности конструирования учебных материалов, оценка полученных результатов конструирования |
самооценка полученных результатов конструирования |
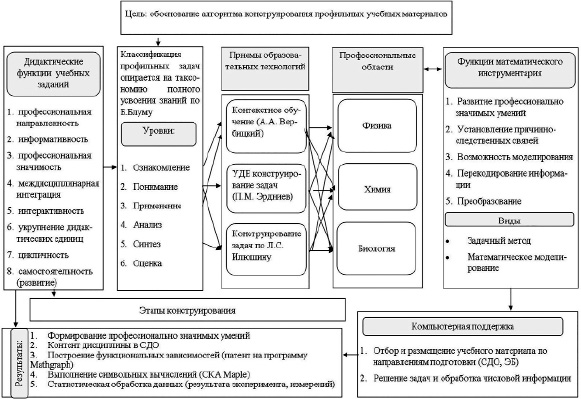
Модель методики конструирования профильных учебных материалов
В модели конструирования профильных учебных материалов определены дидактические функции учебных материалов: профессиональные направленность и значимость, информативность, интерактивность процесса их построения, УДЕ, самостоятельность (рисунок).
В таблице представлена деятельность субъектов практико-ориентированного обучения математике студентов естественно-научных направлений в процессе конструирования профильных учебных материалов.
В процессе практико-ориентированного обучения математике применялись информационные технологии для:
− графического построения функциональных зависимостей, получаемых в процессе конструирования (табличный процессор Excel, система компьютерной математики Maple, а также программа Mathgraph, в процессе разработки которой принял участие и автор статьи) [13];
− представления учебной информации и осуществления текущего контроля знаний (система дистанционного обучения на платформе Moodle, Google-формы);
− совместной работы в онлайн-режиме (интерактивная доска Miro).
Выводы
Практико-ориентированное обучение математике направлено на достижение понимания студентами сущности изучаемых математических понятий, функциональность этих знаний в профессиональной подготовке. Процесс конструирования профильных учебных материалов формирует умения применять математические знания, осуществляя перенос сформированных умений на решение практических задач экспериментального и исследовательского характера на последующих этапах обучения студентов в вузе, включая итоговые государственные испытания. Определенный на основе компонентного анализа общепрофессиональных компетенций в ФГОС ВО естественно-научных направлений и направления «Математика» состав математического инструментария включает математическое моделирование и задачный метод. Математическое моделирование направлено на установление причинно-следственных связей, прогнозирование изучаемых процессов, результаты моделирования могут быть визуализированы, в том числе и с помощью программных средств. Задачный метод развивает умения выполнять расчеты по видам и уровням профессиональной деятельности, развивает логическое мышление, умение устанавливать причинно-следственные отношения, демонстрирует возможности численных методов. Представленный состав математического инструментария определяет полноту выполнения его функции как средства формирования конкретной практической задачи.
К условиям конструирования учебных материалов средствами математического инструментария относятся:
1. Определение специфики содержания и профессиональной деятельности выпускников (область, сфера деятельности, трудовые функции выпускников).
2. Ориентация на формирование готовности к самостоятельному выбору способов и средств конструирования учебных материалов (составление и преобразование задач, моделирование, самоанализ и др.).
3. Отбор соответствующего инструментария, способного обеспечить процессы конструирования учебного материала. Отбор инструментария осуществляется на основе компонентного анализа общепрофессиональных компетенций и обобщенных трудовых функций, выбора среди них наиболее значимых для формирования фонда тестовых заданий на основе сопряжения требований образовательных и профессиональных стандартов.
4. Отбор профильного содержания для конструирования профильных учебных материалов (задач, кейсов, заданий), выбор типа ресурсов для отбора содержания и соответствие профессиональной значимости для направления подготовки.
5. Выбор дидактических приемов для конструирования учебных заданий, их анализ и самоанализ (приемы укрупнения дидактических единиц П.М. Эрдниева, контекстного обучения А.А. Вербицкого, конструктор задач Л.С. Илюшина).
6. Компьютерная поддержка реализации конструирования и оценивания полученных учебных материалов.
7. Диагностика корректности конструирования учебных материалов, оценка и самооценка полученных результатов конструирования.
8. Создание банка учебных заданий и методических рекомендаций в системе дистанционного обучения, электронной библиотеке, соответствие их учебным планам и образовательной программе соответствующего направления подготовки.
9. Взаимодействие преподавателей профильных и математических дисциплин для сопряжения учебных планов.



