На современном этапе инновационных преобразований актуальны вопросы применения современных математических методов и программных систем для решения задач в различных сферах деятельности человека. Вопросам моделирования посвящен ряд научных трудов [1, 2]. Задачи построения адекватных моделей сложных экономических объектов не потеряли своей актуальности в силу их большого разнообразия. Принятие управленческих решений предполагает наличие информации о текущем состоянии объекта управления и некоторой модели, дающей представление о поведении объекта при меняющихся условиях эксплуатации и изменяющихся внешних условиях. Созданию моделей, учитывающих все особенности объекта моделирования, посвящено в настоящее время достаточно много исследований [3–5]. Благодаря бурному развитию информационных технологий появилась возможность создавать новые виды моделей, использующие существующие возможности вычислительных систем.
Пользуясь классификацией, предложенной американским профессором Лотфи Заде [6], наиболее изученные математические модели реализуют жесткие вычисления, основанные на строгих алгоритмах проведения вычислений. Особенностью современного этапа использования таких моделей является возможность работы с большими данными, требующими специальных алгоритмов обработки и значительных вычислительных мощностей. Наиболее известные в этом классе регрессионные модели используют для построения статистические данные и основаны на выборе структуры модели, расчете параметров и оценки статистических свойств.
Чаще всего точное математическое описание сложных объектов не может быть получено ввиду большой размерности задачи, неполноты информации о нем, отсутствия априорных сведений о функциональной связи входных параметров и выходной величины. В таких случаях используются различные методы построения модели объекта на основе данных о его поведении при различных входных воздействиях. Профессором Лотфи Заде был предложен новый подход, основанный на понятии нечеткой логики [7]. Методология, основанная на нечеткой логике, получила название мягких вычислений. Каждый человек чаще всего принимает решения на основе неполной информации и приблизительных сведений, что не мешает ему достигать поставленных задач. В этой связи можно сделать вывод, что нечеткая логика в принятии решений приближается к естественному процессу, свойственному человеку, и является более гибким подходом к построению модели [8].
Основное отличие нечеткой логики от булевой состоит в том, что переменные принимают значения в интервале от 0 до 1, в то время как в булевой логике возможны только два значения. Значения нечеткой переменной при этом могут быть заданы различными способами: нечеткого числа, лингвистической переменной или совокупности правил. В настоящее время разработаны и находят практическое применение различные алгоритмы нечеткого вывода. Одной из возникающих вычислительных проблем является усложнение алгоритмов нечеткого вывода при большом числе рассматриваемых переменных. В связи с этим стоит задача выбора наиболее эффективного подхода к выбору алгоритмов нечеткого логического вывода, позволяющего сократить размерность вычислительного алгоритма.
Цель исследования – анализ и разработка алгоритмов нечеткого логического вывода в условиях большого числа входных факторов.
Материалы и методы исследования
В качестве материалов исследования в данной работе использованы статьи, монографии, электронные интернет-ресурсы, посвященные тематике разработки и использования алгоритмов нечеткого логического вывода. В качестве методов проведения исследований применялись методы дискретной математики, теории множеств, алгоритмы и методы численного моделирования. Моделирование алгоритмов нечеткой логики выполнено в среде Python с использованием библиотеки FuzzyWuzzy.
Результаты исследования и их обсуждение
Анализ публикаций по вопросам практического применения методов нечеткого логического вывода позволяет выделить среди известных подходов алгоритм Мамдани. В качестве основного элемента алгоритма Мамдани используется нечеткая переменная, которая может быть представлена кортежем (β, T, X, A, μA (x)), где
β – имя нечеткой переменной (лингвистическое);
T – возможные значения переменной β;
X – возможные значения входной переменной;
A – нечеткое множество, привязанное к лингвистической переменной;
μA (x) – функция принадлежности множеству A.
Функции принадлежности, задающие нечеткое множество, могут быть заданы различными зависимостями. Чаще всего для этих целей используются кусочно-линейные функции, что связано с простотой их вычисления. Примеры наиболее распространенных вариантов функций принадлежности приведены в таблице.
Разработка функции принадлежности для заданного множества является наименее формализованным элементом алгоритмов нечеткой логики. Существует много различных подходов, но все они в той или иной степени связаны с экспертным оцениванием. С другой стороны, точное задание функций принадлежности для рассматриваемых задач не требуется, достаточно определить наиболее характерные значения и вид функции. Для построения функций принадлежности в ряде задач используются нейросетевые методы.
Функции принадлежности в системах нечеткого вывода
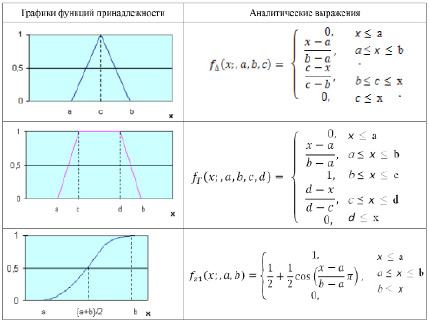
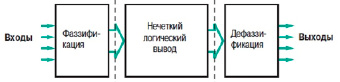
Рис. 1. Основные этапы процедуры нечеткого логического вывода
Алгоритм Мамдани основан на использовании базы правил, с помощью которой осуществляется формирование нечеткого множества.
если х есть А1 И у есть В1, то z есть C1; (1)
если х есть А2 И у есть В2, то z есть C2, (2)
где х, y – входные переменные; z – выходная переменная; А1, А2, B1, B2 – нечеткие множества для входных переменных; С1, С2, – нечеткие множества выходной переменной.
Построение модели заключается в определении оптимальных параметров правил и функций принадлежности системы нечеткого вывода. Алгоритм состоит из нескольких последовательных этапов. Укрупненно он может быть представлен в виде схемы на рис. 1.
На этапе фаззификации происходит определение степени принадлежности входных факторов нечетким множествам путем использование выбранных функций принадлежности.
Популярность подхода Мамдани обусловлена простотой использования опыта оператора, формирующего базовые правила фаззификации. Большинство предлагаемых алгоритмов нечеткого логического вывода используют базовые элементы алгоритма Мамдани, хотя и имеют свои особенности.
Одним из таких алгоритмов является подход, предложенный Такаги Сугено. Особенность этого подхода в формировании набора правил базы знаний. Сугено использует конструкцию логического вывода на основе линейной свертки. Правило в подходе Сугено выглядит следующим образом:
если x есть A1 И y есть B1, то z = a1x+b1 y, (3)
если x есть A2 И y есть B2, то z = a2x+b2 y, (4)
где А1, А2, B1, B2 – нечеткие множества для входных переменных x и y; z – выходная переменная; a1, a2, b1, b2 – коэффициенты линейной свертки.
Системы, основанные на алгоритмах Сугено, в большей степени проявляют свою эффективность при моделировании нелинейных зависимостей. Последнее обстоятельство объясняет широкое применение этих алгоритмов в управлении техническими системами. Проведенные эксперименты по моделированию линейных зависимостей для алгоритмов Мамдани и Сугено не выявили большой разницы в точности и быстродействии.
Общую структуру систем нечеткого логического вывода можно представить в виде типовой структуры (рис. 2). Фаззификатор преобразует входные факторы в нечеткие значения β, поступающие на вход машины логического вывода. В результате выполнения процедуры логического вывода на выходе значения γ также являются нечеткими значениями. Дефаззификатор преобразует значения γ в четкие значения, выполняя функцию приведения к четкости.
Различие подходов и алгоритмов нечеткого логического вывода чаще всего проявляется в выборе метода реализации дефаззификатора. Наиболее простым методом можно считать метод максимума, в котором выход системы (y) определяется как максимум функции принадлежности для треугольной и как среднее значение верхней части для трапецеидальной функции. Кроме того, используется метод центра площади и метод центра тяжести под кривой функции принадлежности.
Преимуществами рассмотренного подхода являются универсальность, простота интерпретации полученной модели вследствие использования языка, близкого к естественному, возможность использования априорной информации об объекте. Однако представление модели в качестве системы нечеткого логического вывода обладает и определенными недостатками, основным из которых является субъективность получаемого результата, поскольку набор нечетких правил формируется экспертом. Вследствие этого предлагается использовать адаптивные системы нечеткого вывода, для которых набор правил и параметры, сформулированные экспертом, подвергаются дальнейшему уточнению на основании выборки данных о поведении входных и выходных переменных объекта.
Другая сложность при реализации указанных алгоритмов связана с решением задач в многомерном пространстве входных переменных. Это связано с тем, что точность получаемой модели значительным образом определяется количеством функций принадлежности каждой переменной. Увеличение количества переменных и их функций принадлежности, в свою очередь, приводит к возрастанию числа нечетких правил и значительному увеличению количества вычислений, а следовательно, времени и вычислительных ресурсов, требуемых для определения параметров модели и ее дальнейшего использования.
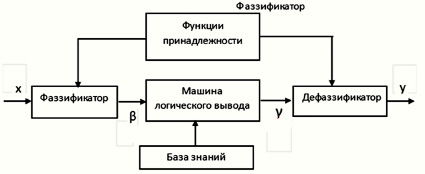
Рис. 2. Общая структура системы нечеткого логического вывода
Также следует учитывать, что при исследовании и построении моделей реальных объектов имеющаяся информация об объекте может быть и избыточной – часть входных параметров, отраженных в выборке данных, может вообще не влиять или оказывать очень слабое влияние на поведение объекта. Однако при создании нечеткой модели с использованием таких алгоритмов данный фактор никак не уменьшает размерность решаемой задачи и количество вычислений. Таким образом, алгоритмы построения нечетких моделей, построенные по классическому принципу, часто не обладают желаемой гибкостью, требуемой для эффективного решения разнообразных задач такого рода.
В качестве решения указанных задач предлагается использование адаптивных многоэтапных алгоритмов, аналогичных методу группового учета аргументов (МГУА) [8]. Данный подход позволяет широко использовать возможности структурной идентификации создаваемой модели, а также учитывать неоднородность влияния входных переменных на исследуемый отклик объекта.
В классическом МГУА в качестве частных моделей используются многочлены различного вида. Однако использование систем нечеткого вывода с двумя входными переменными позволяет существенно повысить скорость сходимости алгоритма, особенно при построении моделей сложных зависимостей, так как такие системы обладают лучшими аппроксимирующими свойствами. Определение параметров таких частных моделей может производиться различными известными методами настройки параметров систем нечеткого вывода, например, при помощи метода наращивания или гибридного алгоритма. Пример структуры модели, получаемой в результате применения такого подхода, показан на рис. 3.
С целью проверки эффективности данного алгоритма было проведено моделирование ряда сложных аналитических зависимостей. В процессе моделирования проведено сравнение результатов применения вышеописанного подхода и классических подходов Мамдани и Сугено. Подход с применением систем нечеткого вывода позволил выявить значимые входные воздействия, эти результаты совпали с результатами, полученными другими методами. Однако разработанный метод позволил также, с использованием полученной модели объекта, точнее определить характер зависимости отклика от каждого из входов, а также осуществлять прогнозирование выходной величины по набору входных параметров.
Разработанный подход позволяет использовать достоинства систем нечеткого логического вывода и, кроме того, преимущества различных методов структурной и параметрической идентификации систем. При этом он значительным образом расширяет возможности структурной оптимизации и позволяет адаптировать структуру разрабатываемой модели в зависимости от характера исследуемой зависимости. Предлагаемый алгоритм позволяет разбить процесс построения модели на несколько этапов – рядов селекции.
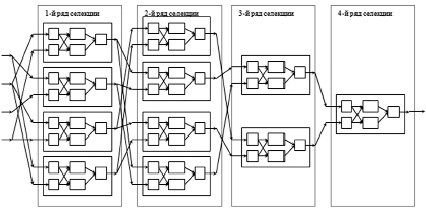
Рис. 3. Структура системы, созданной при помощи алгоритма МГУА Источник: составлено авторами
В ходе выполнения каждого этапа могут быть оценены полученные результаты, внесены соответствующие корректировки в параметры, определяющие ход процесса оптимизации. При применении описанного выше метода входными переменными для частных моделей являются выходные значения, полученные системами предыдущего ряда. Такой подход соответствует классическому подходу МГУА.
Выводы
Проведенные исследования позволили сделать следующие выводы:
1. Для задач прогнозирования в системах нечеткого логического вывода наиболее универсальной является процедура вывода на основе алгоритма Сугено.
2. Недостатком существующих подходов формирования структуры системы нечеткого логического вывода является большая размерность структуры системы при числе входных параметров более 4–5 и, как следствие, большие вычислительные затраты на обработку данных и настройку системы.
3. Точность прогноза системы НЛВ при одном и том же объеме обучающей выборки существенно зависит от расположения экспериментальных точек в области изменения вектора входных переменных. Поэтому имеет смысл говорить по крайней мере о целенаправленном выборе обучающей выборки.
4. При настройке параметров нечетких правил системы НЛВ влияние параметров функций принадлежности в алгоритме Сугено несущественно, и настройку правил можно свести к настройке коэффициентов правой части этих правил.
5. Использование принципов формирования структуры регрессионной модели алгоритма МГУА для синтеза структуры системы НЛВ позволяет существенно упростить задачу, уменьшить вычислительные затраты, использовать аналитические методы для настройки параметров системы.
6. Результаты моделирования разработанного алгоритма позволяют утверждать, что при сравнительно небольших вычислительных затратах предлагаемый алгоритм не уступает в точности прогнозирования как классическим методам, так и процедурам на основе нейронной сети Ванга-Менделя, использующей подход Мамдани.
7. Наиболее предпочтительная область использования данного алгоритма – это задачи прогнозирования при большом числе входных переменных. Именно с увеличением числа входных параметров системы наилучшим образом проявляются положительные свойства данного алгоритма.



