Гиперпараметры в классическом машинном обучении – параметры алгоритма, которые определяются не автоматически, во время обучения, а задаются исследователем непосредственно перед самим обучением модели и не меняются в его процессе. Подбор оптимальных гиперпараметров является важной частью процесса настройки алгоритма, так как они могут существенно повлиять на качество результатов во время тестирования и на скорость обучения.
Известно множество способов автоматического подбора гиперпараметров. Ниже приводятся примеры некоторых из них.
Самым естественным способом подбора гиперпараметров является перебор по сетке со скользящим контролем (GridSearch CV). В его процессе исследователем фиксируются несколько значений требуемых гиперпараметров, после чего алгоритм автоматически перебирает все их комбинации, при этом на каждой из них модель обучается и тестируется. По завершении указанного процесса, выбирается модель, показавшая лучшее качество. Главным недостатком указанного метода является асимптотическое время выполнения, так как в ходе его работы осуществляется прямой полный перебор гиперпараметров, сопровождающийся вычислительно трудоемким скользящим контролем (cross validation).
Если по какой-то причине исследователю требуется перебрать большое число гиперпараметров, то целесообразнее использовать случайный поиск (Random search) [1], в ходе которого для каждого из гиперпараметров выбирается значение из заданного наперед распределения, что помогает в первую очередь перебирать значения наиболее значимых гиперпараметров, которые сильно влияют на качество модели, таким образом с бо́льшей вероятностью находить их удачную комбинацию.
Итеративные методы подбора гиперпараметров, основанные на байесовской оптимизации и их модернизации [2], в отличие от алгоритмов, которые были перечислены выше, тем или иным образом обращаются к результатам предыдущих итераций, но так же, как и методы, основанные на переборе, имеют высокую вычислительную сложность.
Альтернативным подходом к подбору гиперпараметров модели является оптимизация их значений посредством градиентного спуска. Существуют подходы к подбору гиперпараметров конкретных моделей, к примеру определенных архитектур нейросетей [3], или их оптимизаторов, но стоит отметить, что данный подход не получил распространения в рамках классического машинного обучения, несмотря на его большой потенциал.
Целью исследования алгоритмов подбора оптимальных гиперпараметров является повышение эффективности и точности моделей машинного обучения, улучшение их обобщающей способности, сокращение времени и ресурсов, затрачиваемых на обучение, а также упрощение и автоматизация процесса выбора оптимальных параметров.
В этой статье будет рассмотрен универсальный алгоритм подбора гиперпараметров для моделей классического машинного обучения, реализованных в библиотеке scikit-learn, основанный на градиентной оптимизации.
Материалы и методы исследования
Пусть определена модель М, процесс обучения и получаемые в его результате параметры которой детерминированы относительно начального набора ее гиперпараметров h1,h2,…,hn. Пусть h1,h2,…,hn выражаются вещественными числами, а также задана некоторая метрика Q, по которой осуществляется оценивание качества работы модели М на этапе тестирования.
Необходимо разбить набор данных на обучающую и тестовую подвыборки и зафиксировать их, начать обучение модели М на обучающей подвыборке и оценить качество ее работы по метрике Q на тестовой подвыборке. Так как результаты обучения детерминированы относительно h1,h2,…,hn, то каждому набору h1i,h2i,…,hni будет соответствовать единственное значение метрики качества Qi. Значит, можно рассмотреть Q как функцию от h1,h2,…,hn, такую, что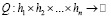 
.
Далее необходимо определить функцию L(h1,h2,…,hn) таким образом, чтобы ее минимизация была эквивалентна задаче улучшения качества по метрике Q (максимизации или минимизации функции Q(h1,h2,…,hn) в зависимости от решаемой задачи и выбранной метрики). Тогда задачу подбора оптимальных гиперпараметров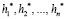 
модели M можно представить следующим образом:
.
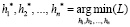Затем предлагается воспользоваться градиентными алгоритмами оптимизации. Градиент в рассматриваемой задаче определяется следующим образом: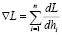
.
Так как на практике большинство численных гиперпараметров классических моделей машинного обучения задается натуральными числами, можно рассматривать следующее численное приближение компонент градиента:
.
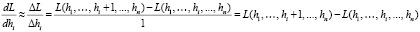Для каждой из компонент градиента предлагается использовать коэффициент масштаба s = bh – ah, где bh, ah – границы заданного пользователем промежутка, на котором осуществляется поиск гиперпараметра h. Данный множитель добавляется с целью масштабирования значений компонент градиента, так как в практических задачах размеры промежутков, в которых с большой долей вероятности будут находиться оптимальные значения различных гиперпараметров, могут сильно отличаться (например, для модели GradientBoosting из scikit-learn гиперпараметр n_estimators на практике, с большой долей вероятности, будет лежать в отрезке [50; 300], а max_depth – в отрезке [2; 7]).
Тогда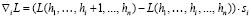 
.
Пусть h = h1,h2,…,hn, а s = h1i,h2i,…,hni.
Градиенты будут рассчитываться следующим образом, с учетом применения коэффициента масштаба s:
1) Классический градиент:
.
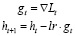Здесь и далее: lr– гиперпараметр оптимизатора, выбираемый пользователем;
t – номер шага спуска.
2) Ускоренный градиент Нестерова [4]:
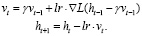
3) Adagrad [5]:
.
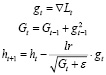Здесь и далее: γ – гиперпараметр оптимизатора, выбираемый пользователем,
– наперед заданное малое число, вводимое во избежание возможного деления на 0.
4) RMSprop [6]:
.
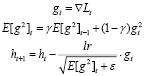5) Adadelta [7]:
.
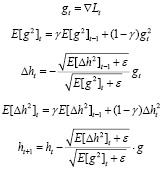6) Adam [8]:
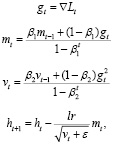
где β1, β2 – гиперпараметры оптимизатора, выбираемые пользователем.
Перед началом работы алгоритма HOptim набор данных разделяется на три части: тренировочная, валидационная и тестовая. На каждой итерации алгоритм оптимизации гиперпараметров обучает полученную модель M с гиперпараметрами h1t,h2t,…,hnt, где t – номер шага, на тренировочной подвыборке, вычисляет компоненты градиента на валидационной подборке, делая предсказание с помощью обученной ранее модели и изменяет гиперпараметры, совершая шаг градиентного спуска. Параллельно с этим вычисляется качество модели на тестовой подвыборке, набор гиперпараметров, обеспечивший лучшие результаты на этапе тестирования, сохраняется.
Подобный подход к вычислению компонент градиента позволяет алгоритму не переобучить модель M путем увеличения ее сложности за счет гиперпараметров, а подобрать такой их набор, который позволит максимизировать качество работы на данных, недоступных в процессе обучения самой модели M, а следовательно, улучшить ее качество на этапе тестирования.
В некоторых случаях предлагается запоминать значения компонент градиентов с целью ускорения работы алгоритма в условии возникновения циклов (для некоторых оптимизаторов это может быть полезно, так как, например, Adam способен через некоторое число итераций выходить из подобных циклов, накапливая «энергию»).
Результаты исследования и их обсуждение
Предложенный метод проходит испытание на классических задачах классификации и регрессии.
Эксперимент: классификация.
В качестве набора данных для классификации используется Telco Customer Churn с предварительно удаленными столбцами, содержащими категориальные признаки. В качестве модели для классификации применена модель scikit-learn GradientBoostingClassifier. Функция, по которой осуществляется спуск, задается следующим образом:
L = 1 – Q (accuracy loss),
где Q – оценка качества работы модели по метрике accuracy score. Здесь и далее в столбец skip записывается количество компонент, вычисления которых удалось сэкономить благодаря их записи в память, а в столбец not skip – количество вычисленных компонент. Этот и следующие эксперименты проводятся на процессоре Intel Core i5.
Классификация: плохие начальные гиперпараметры.
В этом эксперименте начальные значения гиперпараметров приняты равными единице.
Варьируемые гиперпараметры: max_depth, n_estimators.
Максимальное число шагов: 50.
Начальный accuracy score модели: 0,725
Результаты применения HOptim показаны в табл. 1 и на рис. 1, 2.
Таблица 1
Результаты применения HOptim
|
Оптимизатор |
Лучший acc. score |
Время, c |
lr |
γ |
β1 |
β2 |
skip |
not skip |
|
Класс. град. |
0,797 |
3,60 |
5 |
нет |
нет |
нет |
135 |
16 |
|
Г. Нестерова |
0,799 |
96,2 |
10 |
0,7 |
нет |
нет |
114 |
37 |
|
Adagrad |
0,803 |
58,60 |
0,4 |
нет |
нет |
нет |
113 |
38 |
|
RMSprop |
0,804 |
145,50 |
0,2 |
0,7 |
нет |
нет |
74 |
77 |
|
Adadelta |
0,796 |
25,20 |
нет |
0,4 |
нет |
нет |
125 |
26 |
|
Adam |
0,804 |
152,20 |
0,3 |
нет |
0,4 |
0,6 |
68 |
83 |
Источник: составлено авторами.
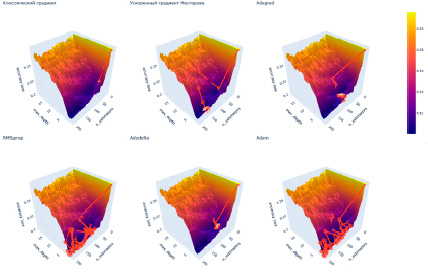
Рис. 1. Поверхность функции потерь для набора данных Telco Customer Churn и модели GradientBoostingClassifier – работа оптимизаторов Источник: составлено авторами
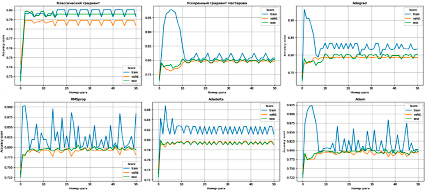
Рис. 2. Accuracy score модели GradientBoostingClassifier в зависимости от шага и выбранного оптимизатора Источник: составлено авторами
Результаты, отраженные в табл. 1, показывают, что оптимизаторы RMSprop и Adam наиболее качественно справляются с задачей. В дополнение можно отметить, что эти оптимизаторы не попадают в цикл, что позволяет им перебрать большее количество комбинаций гиперпараметров (рис. 1, 2).
Классификация: GridSearch CV + HOptim
Перед использованием HOptim гиперпараметры были предварительно подобраны с помощью GridSearch CV.
Варьируемые гиперпараметры: max_ depth, n_estimators, min_samples_split, min_samples_ leaf.
Максимальное число шагов: 50.
Начальный accuracy score модели: 0,795
Результаты применения HOptim показаны в табл. 2 и на рис. 3.
Видно, что в этой задаче результаты работы алгоритма HOptim с неудачной стартовой позиции и с более удачной позиции, найденной с помощью GridSearch CV, различаются слабо, но стоит отметить, что лучший результат в ходе эксперимента достигнут ускоренным градиентом Нестерова в связке с GridSearch CV (табл. 2 и рис. 3).
Эксперимент: регрессия.
Рассматривается применение предложенного алгоритма на примере задачи регрессии.
В качестве набора данных для регрессии используется House prices regression с предварительно удаленными столбцами, содержащими категориальные признаки. В качестве модели для регрессии применяется модель skelearn GradientBoostingRegressor. Функция, по которой осуществляется спуск, задается следующим образом: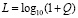 
(log MSE loss), где Q – среднеквадратичная ошибка модели.
Регрессия: плохие начальные гиперпараметры.
В этом эксперименте начальные значения гиперпараметров приняты равными единице.
Таблица 2
Результаты применения HOptim
|
Оптимизатор |
Лучший acc. score |
Время, c |
lr |
γ |
β1 |
β2 |
skip |
not skip |
|
Класс. град. |
0,797 |
71,6 |
10 |
нет |
нет |
нет |
177 |
74 |
|
Г. Нестерова |
0,809 |
196,8 |
10 |
0,95 |
нет |
нет |
76 |
175 |
|
Adagrad |
0,8043 |
263,3 |
0,5 |
нет |
нет |
нет |
63 |
188 |
|
RMSprop |
0,803 |
324,7 |
0,1 |
0,8 |
нет |
нет |
51 |
200 |
|
Adadelta |
0,804 |
309,2 |
нет |
0,6 |
нет |
нет |
60 |
191 |
|
Adam |
0,8014 |
241,2 |
0,1 |
нет |
0,6 |
0,7 |
50 |
201 |
Источник: составлено авторами.
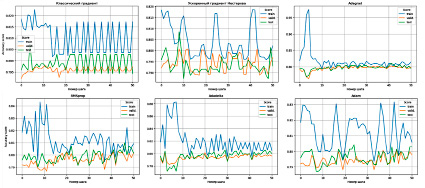
Рис. 3. Accuracy score модели GradientBoostingClassifier в зависимости от шага и выбранного оптимизатора. Источник: составлено авторами
Таблица 3
Результаты применения HOptim
|
Оптимизатор |
Лучший log MSE loss |
Время, c |
lr |
γ |
β1 |
β2 |
skip |
not skip |
|
Класс. град. |
9,075 |
17,10 |
2 |
нет |
нет |
нет |
78 |
73 |
|
Г. Нестерова |
9,000 |
65,4 |
2 |
0,85 |
нет |
нет |
66 |
85 |
|
Adagrad |
9,001 |
21,00 |
0,4 |
нет |
нет |
нет |
97 |
54 |
|
RMSprop |
9,000 |
39,90 |
0,2 |
0,5 |
нет |
нет |
82 |
69 |
|
Adadelta |
9,045 |
9,70 |
нет |
0,35 |
нет |
нет |
114 |
37 |
|
Adam |
8,996 |
46,40 |
0,3 |
нет |
0,4 |
0,6 |
66 |
85 |
Источник: составлено авторами.
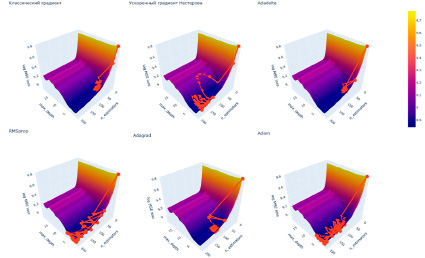
Рис. 4. Поверхности функции потерь для набора данных House prices regression и модели GradientBoostingRegressor Источник: составлено авторами
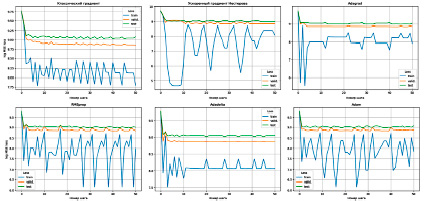
Рис. 5. Log MSE loss модели GradientBoostingClassifier в зависимости от шага и выбранного оптимизатора Источник: составлено авторами
Варьируемые гиперпараметры: max_depth, n_estimators.
Максимальное число шагов: 50.
Начальный log MSE loss модели: 9,771
Результаты применения HOptim показаны в табл. 3 и на рис. 4, 5.
Результаты, отраженные в табл. 3, показывают, что градиент Нестерова и RMSprop наиболее качественно справляются с задачей, минимизируя функцию потерь лучше других оптимизаторов.
Важно отметить, что градиент Нестерова более подвижен, чем другие оптимизаторы в этой задаче, что позволяет ему осуществить оценку большего количества комбинаций гиперпараметров, что наглядно представлено на рис. 4, 5.
Регрессия: GridSearch CV + HOptim
Перед использованием HOptim гиперпараметры были предварительно подобраны с помощью GridSearch CV.
Варьируемые гиперпараметры: max_ depth, n_estimators, min_samples_split, min_ samples_leaf.
Максимальное число шагов: 50.
Начальный log MSE loss модели: 9,278
Результаты применения HOptim показаны в табл. 4 и на рис. 6.
В описанном эксперименте наилучшие гиперпараметры найдены алгоритмом HOptim без использования GridSearch CV (табл. 4 и рис. 6).
В большинстве случаев целесообразно сначала использовать GridSearch CV или любой другой алгоритм подбора гиперпараметров с большим шагом, после чего использовать HOptim с малым коэффициентом lr. В случае, если решение, найденное GridSearch CV, будет находиться рядом с минимумом функции потерь, то HOptim позволит улучшить результат, осуществляя поиск в окрестности найденного решения.
Таблица 4
Результаты применения HOptim
|
Оптимизатор |
Лучший log MSE loss |
Время, c |
lr |
γ |
β1 |
β2 |
skip |
not skip |
|
Класс. град. |
9,198 |
119,8 |
2 |
нет |
нет |
нет |
109 |
142 |
|
Г. Нестерова |
9,095 |
145,2 |
0,7 |
0,8 |
нет |
нет |
144 |
107 |
|
Adagrad |
9,108 |
142,4 |
0.1 |
нет |
нет |
нет |
54 |
197 |
|
RMSprop |
9,1922 |
219,2 |
0.1 |
0.8 |
нет |
нет |
50 |
201 |
|
Adadelta |
9,1778 |
234,7 |
нет |
0.6 |
нет |
нет |
51 |
200 |
|
Adam |
9,06137 |
92,2 |
0.1 |
нет |
0.6 |
0.7 |
99 |
152 |
Источник: составлено авторами.
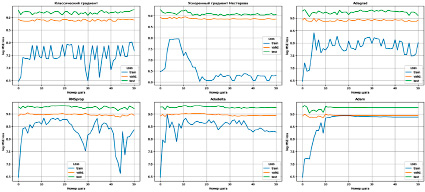
Рис. 6. Log MSE loss модели GradientBoostingClassifier в зависимости от шага и выбранного оптимизатора Источник: составлено авторами
Заключение
В статье рассмотрена задача оптимизации гиперпараметров в рамках классического машинного обучения, кратко описаны наиболее распространенные методы подбора гиперпараметров и механизм их работы. Предложен алгоритм HOptim градиентной оптимизации гиперпараметров моделей классического машинного обучения из python-библиотеки scikit-learn, использующий в своей основе оптимизаторы первого порядка. В экспериментах показана эффективность метода HOptim и результативность его совместной работы с алгоритмом подбора гиперпараметров GridSearch CV с большим шагом сетки.
Описанный подход универсален и может быть использован на практике для улучшения качества работы моделей машинного обучения. Подбор оптимальных гиперпараметров позволяет увеличить точность предсказаний моделей. Это особенно важно в задачах классификации и регрессии, где точность работы моделей играет решающую роль.