Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Задача изучения процессов развития региональных социально-экономических систем (СЭС) остается актуальной, особенно в условиях наличия кризисных явлений различного масштаба в них и необходимости принятия оперативных решений при планировании, прогнозировании и управлении такими системами. Получение практически значимых результатов в сфере социально-экономического анализа и прогнозирования развития регионов, территорий, кластеров и других крупных социально-экономических систем затруднительно без использования методов математического моделирования и автоматизированных информационно-аналитических систем. При этом эффективность применения указанного инструментария достигается при выполнении принципа модельной и IT-сбалансированности, суть которого кратко можно выразить так: наличие обеих составляющих – математической модели и автоматизированного программно-аналитического комплекса – не гарантирует эффективного анализа изучаемых процессов и систем, требуя их согласованного взаимодействия. Или иначе: не всякая математическая модель позволяет извлечь из нее знание об изучаемом объекте без возможности автоматизировать анализ больших объемов циркулирующей в ней информации, и, наоборот, автоматизированные средства компьютерного анализа информации могут оказаться бесполезными в отсутствие адекватной математической модели объекта или наличия модели, расчеты по которой затруднены в условиях реальных прикладных задач. В настоящее время при моделировании крупных СЭС используются комбинации динамических и статических моделей [1, с. 11–12; 2, с. 19, 176]. При этом сохраняется и значительный поток публикаций, описывающих различные методы анализа региональных моделей СЭС. Например, в работе [3] описано применение агент-ориентированных моделей региона в рамках метода имитационного моделирования, в [4] рассматриваются макроэкономические, а в [5] – мезоэкономические особенности функционирования региона, работа [6] содержит краткие обзоры различных моделей региона, а [7] – описание моделей активного управления социально-экономическими системами. При этом большинство публикаций касается либо отдельных концептуальных вопросов, вопросов моделирования, разработки алгоритмов численного анализа моделей, и, соответственно, имеется незначительное количество работ системного характера, например [8], в которых рассматривается весь взаимоувязанный комплекс аналитических инструментов – концепция, математические модели, методы и алгоритмы их анализа, объединяемые в автоматизированные системы поддержки принятия решений (СППР). Следует отметить, что математические модели в приведенных выше публикациях имеют ряд особенностей, зачастую затрудняющих разработку соответствующих СППР, ориентированных на оперативную экспертную поддержку оптимальных решений при управлении развитием региональных СЭС или выявление оптимального баланса циркулирующих в них потоков. В частности, в агент-ориентированных моделях региона [3] акцент делается на имитационное моделирование поведения децентрализованных агентов в регионе, и напрямую не ставится задача выявления оптимальных параметров функционирования региона. В моделях [4; 5] рассматривается динамика экономического процесса в форме системы соотношений Р. Соллоу с заранее заданной возрастающей производственной функцией (преимущественно в форме Кобба – Дугласа), не выявляющей жизненный цикл развития региона. При построении модели работы [6] используется концепция межотраслевого баланса, имеющая ряд критических замечаний с точки зрения корректности использования открытой статистической информации о функционировании экономики региона. Динамическая модель, описанная, например, в [7], не является оптимизационной, а модель [8] является примером нелинейных задач экономической динамики, в которых, вообще говоря, затруднен их численный анализ, особенно в случае большой размерности решаемых задач.

Целью данного исследования является построение многокритериальной оптимизационной социо-эколого-экономической модели такой крупной организационной системы, как социально-экономический регион, с учетом его управленческой, социальной и экологической составляющих.

Материалы и методы исследования

При моделировании крупных СЭС необходимо учитывать многочисленные особенности этих систем: динамический характер, наличие многих участников, сложную взаимозависимость экономических, социальных, экологических, управленческих процессов, характеристики материальных и финансовых потоков (их структуру, стратегические и тактические составляющие), наличие многочисленных рисков функционирования. Это требует применения соответствующих принципов, моделей, методов и алгоритмов их анализа и синтеза, адекватно отражающих эти особенности. К указанным принципам, помимо упомянутого выше принципа модельно-алгоритмической сбалансированности, необходимо отнести принципы оптимизационности и многокритериальности.

Принимая во внимание предмет исследования (региональные социально-экономические процессы), полноценное описание функционирования региона требует использования динамических моделей [9, гл. 3]. Кроме того, необходимость принятия эффективных управленческих решений инвестиционного, производственного, финансового характера обуславливает и необходимость применения оптимизационного подхода, позволяющего принимать решения с учетом возможности выявления экономического потенциала (максимальных возможностей) СЭС [2, с. 9]. Все вместе приводит к выводу, что в идеале требуется решение оптимизационных динамических задач очень большой размерности, анализ которых с помощью автоматизированных информационных систем до сих пор встречает значительные трудности, в том числе вычислительного характера (например, накопление ошибок округления при использовании итерационных методов или зацикливание при реализации точных методов). В этой связи при решении динамических оптимизационных задач целесообразно применение методов идеализации, абстрагирования, агрегирования и других методологических приемов, суть которых сводится к упрощению описываемых процессов, выделению основных (ключевых) процессов, осреднению их характеристик на несколько подпроцессов и/или периодов времени (в том числе на один) и др. К таким приемам можно отнести линеаризацию моделей (рассмотрение линейной динамики по искомым переменным), алгоритмов анализа, переход к статическим версиям (когда многошаговая во времени задача рассматривается как одношаговая) и др.

В данной работе при моделировании и исследовании региона используется линейная, трехкритериальная одношаговая модель оптимального управления, алгоритмы и методы дисконтирования и структурирования (по доходно-расходным, тактико-стратегическим и т.п. признакам) финансовых потоков, агрегирования, усреднения характеристик активов, продукции, выделения этапов функционирования и др. Концепция построения математической модели при проведении данного исследования опубликована в работе [1, с. 10–32] с модификациями, изложенными в [2, с. 16–34].

Пусть n – количество производственных подразделений, видов производимой в регионе продукции и основных производственных фондов (ОПФ) производственных подразделений для ее производства (используется принцип «чистых отраслей»: на каждом ОПФ производственного подразделения производится один вид продукции (товара или услуги)), k = 1, …, n – порядковый номер производственного подразделения, его ОПФ, производимой продукции. Производимая в регионе продукция и соответствующие ОПФ производственного подразделения характеризуются следующим набором показателей:

Pk – цена единицы продукции k-го вида (денежных единиц за единицу продукции, д.е. / ед. прод);

qk – стоимостной спрос на продукцию k-го вида (денежных единиц, д.е.);

сk – cтоимость ОПФ k-го производственного подразделения (денежных единиц за комплект ОПФ, д.е. / ед ОПФ);

Тk – срок службы ОПФ k-го производственного подразделения (единиц времени, ед. врем.);

Vk – производительность ОПФ k-го производственного подразделения (ед. прод. / ед. ОПФ);

δk = PkVk/сk – фондоотдача ОПФ k-го производственного подразделения. Особенности производства продукции учитываются с помощью следующих показателей:

βk – доля от суммы всех производственных затрат k-го производственного подразделения, используемая для оплаты труда (зарплатоемкость производства);

pk – доля материальных затрат k-го производственного подразделения в сумме всех производственных затрат (материалоемкость производства);

ξk, Dk – соответственно удельный и предельно допустимый объемы выбросов загрязняющего окружающую природную среду (ОПС) вещества при производстве k-й продукции.

При функционировании региона рассматриваются следующие виды налогов для каждого из его производственных подразделений, а также для населения:

N1 – налог на добавленную стоимость (НДС);

N2 – налог на имущество (НИ);

N3 – налог на прибыль (НП);

N4 – страховые взносы производителя в социальные фонды (СВСФ);

N5 – налог на доходы физических лиц (НДФЛ);

N6 – иные, пропорциональные объемам производства, налоговые и неналоговые затраты (например, налог на добычу полезных ископаемых, транспортный, земельный налог и прочие платежи), учитываемые в зависимости от специфики региона и основных реализуемых в нем проектов;

αik, i = 1, …, 6 – ставки, соответствующие указанным налогам и сборам;

αsk – ставка экологического сбора.

Следует отметить, что для различных производственных подразделений региона могут применяться различные формы налогообложения – от полных схем до упрощенных форм изъятий единого налога, что обуславливает использование векторных значений конкретных налогов (для каждого производственного подразделения). То же касается и ставки экологического сбора в связи с тем, что каждый вид производства в регионе может быть дифференцирован по производимому им уровню экологических загрязнений.

Примем, что экономическими агентами в регионе являются производственный (Р) и потребительский (С) секторы экономики, а также управляющий (налоговый) центр (Т).

В качестве критериев эффективности функционирования экономических агентов принимаются максимумы потоков стратегического (как правило, долгосрочного) характера, рассматриваемые ими как жизненно необходимые. Для производителя таковыми считаются прибыль, для потребителя – поток заработной платы, для налогового центра – налоговые потоки. Предполагается, что каждый участник регионального социо-эколого-экономического процесса обладает начальными собственными средствами DSP, DSС, DSТ, а их текущая деятельность, связанная с финансированием оборотных затрат, может кредитоваться, соответственно, под ставки r0P, r0C, r0T на сроки Т0P, Т0C, Т0T. Кроме того, проект развития региона описывается следующими параметрами: T – горизонт планирования (в единицах времени, ед. врем); r – номинальная ставка дисконтирования, учитывающая инфляцию и требования инвестора (кредитора); rэ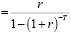 – эффективная ставка дисконтирования в предположении постоянства потоков стратегических доходов на горизонте Т; κ – доля дотаций производителю от налогового центра; 1-κ – доля дотаций потребителю от налогового центра; νk – удельное (нормативное) годовое потребление продукции k-го вида на одного человека в виде доли выручки от продажи k-й продукции (единиц продукции на человека, ед. пр. /чел.), N – численность населения (человек, чел.) региона. Ограничения функционирования региона представлены в таблице.

Обозначим следующие искомые переменные: хk – оптимальный объем (в д.е.) инвестиций в ОПФ k-го производственного подразделения (д.е.); хn+1 – оптимальный объем (в д.е.) дотаций в регион; хn+2, хn+3, хn+4 – оптимальный объем (в д.е.) кредитов производителю, потребителю и налоговому центру региона соответственно.

С учетом введенных обозначений рассмотрим следующую оптимизационную, трехкритериальную математическую модель оценки экономической эффективности региона в матричной форме трехкритериальной задачи линейного программирования:

A(3n+9)×(n+4)‧x(n+4)×1 ≤ B(3n+9)×1; x(n+4)×1 ≥ 0;

J = (c(P), c(C), c(T)→max (*)

где A =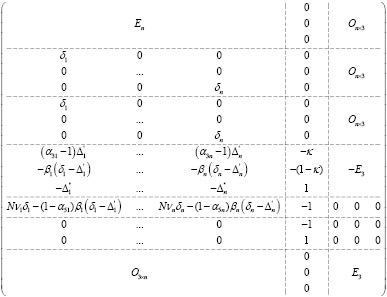

Оn, О3×n, Оn×3 – нулевые матрицы указанных нижними индексами размеров,

Еn, Е3 – единичные матрицы указанных размеров,

,

,

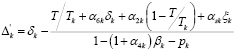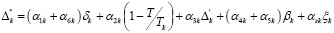B(3n+9)×1=(I1,…,In;q1,…,qn;P1D1/ξ1,…,PnDn/ξn;DSP,DSС,DSТ;0;-Dotmin,Dotmax;Crmax1,Crmax2,Crmax3)T;

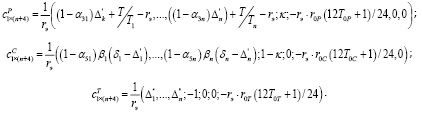
Ограничения функционирования региона

Результаты исследования и их обсуждение

В представленной модели первые n строк матрицы А и, соответственно, компонент вектора b отвечают ограничениям на объемы инвестиций в ОПФ k-й продукции, следующие n строк матрицы А и, соответственно, компонент вектора b – ограничения на спрос, и, наконец, 3-я группа из n строк А и компонент b – экологические ограничения на объем производимой продукции. Строки 3n+1, 3n+2, 3n+3, 3n+4 матрицы А и соответствующие компоненты вектора b соответствуют условиям платежеспособности производителя, потребителя и управляющего центра, а также условию покрытия потребительской корзины уровнем доходов потребителя в форме заработной платы от производителя; строки 3n+5,…,3n+9 и соответствующие компоненты вектора b – условия ограниченности дотаций и кредитов. Учитывая линейность построенной модели, ее можно свести к эквивалентной ей, однокритериальной, с выпуклой линейной сверткой критериев Jсв=μ1с(Р)+μ2с(С)+μ3с(Т). Как задача, имеющая в качестве допустимого множества непустой компакт (легко проверяется принадлежность тривиального решения допустимому множеству), (*) разрешима и может быть подвергнута многопараметрическому и многокритериальному анализу с помощью, например, пакета [10]. Представленная модель обобщает модели, построенные в [1; 2], учитывая экологические ограничения производства в регионе, а также потребительскую корзину населения. С другой стороны, она является частным случаем указанных моделей в предположении максимального использования производственных мощностей рассматриваемых региональных производственных подразделений.

Заключение

Взаимосвязанное и взаимодополняющее использование модели (*), вкупе с программным инструментарием ее автоматизированного анализа, позволяет в перспективе рассматривать ее как основной элемент системы поддержки принятия решений в сфере управления регионом с большим количеством производственных подразделений (предприятий, отраслей, видов экономической деятельности), а также применять инструментально-аналитический комплекс для получения оптимальных характеристик развития региона как организационной системы, в аспекте решения планово-прогнозных задач его развития. Следует подчеркнуть, что идентичные по своей математической сути (одно- и многошаговые линейные задачи математического программирования) модели крупных региональных социально-экономических систем рассмотрены в работах, приведенных в списке литературы, и в них получены нетривиальные решения. Это позволяет обоснованно рассчитывать на возможности включения представленной социо-эколого-экономической модели в автоматизированные системы поддержки принятия решений для эффективного управления современным социально-экономическим регионом.