Композитные материалы часто используются в конструкциях, где способность адаптировать такие свойства, как жесткость и прочность, делает их привлекательными по сравнению с традиционными инженерными материалами. В дополнение к конструкционным применениям композиты также используются в тех областях, где важны как тепловые, так и структурные свойства. Следовательно, сопряженный термоструктурный анализ тонких структур становится все более важным с точки зрения моделирования [1, c. 1–16].
В данной работе многослойная композитная оболочка, подвергнутая воздействию источника тепла с направленным лучом, анализируется с тепловой и структурной точек зрения. Подход, основанный на теории слоев, используется для моделирования структурной части оболочки. Цель работы – проведение расчета коэффициента теплопроводности на основе правила смешивания перпендикулярно направленных углеродных волокон в эпоксидной смоле; введение свойств углеродного волокна и эпоксидной смолы в компьютерную программу моделирования и симуляции; изучение влияния положения источника тепла на профили напряжений и деформаций.
Одной из основных характеристик композиционных, теплоизоляционных и других видов материалов является коэффициент теплопроводности. Коэффициент теплопроводности волокнистого, высокодисперсного материала зависит от интенсивности тепло-, и массообменных процессов в композитном материале и их протекания, а также он зависит от плотности волокон [2, с. 75–81].
Композитный волокнистый материал из базальтовых горных пород выделяется высокой прочностью, низкой горючестью и неплохой шумоизоляцией. В качестве примера можно рассмотреть базальтовый мат шириной 10 см и с плотностью 100 кг/м3, что равносильно теплоизоляции кирпичной стены толщиной 1,20 м [3, с. 15–24; 4, с. 416–422].
С увеличением размера волокон композита теплопроводность увеличивается. В высокодисперсных волокнах базальта размером 5–15 мкм диаметр микропор между волокнами возрастает, что приводит к повышению конвекционных воздушных потоков. Теплоизоляционные материалы на основе базальтовых волокон обладают коэффициентом теплопроводности 0,032–0,048 Вт/(м2∙K) [5].
Эффективной средой для численной реализации целей данной работы является компьютерная программа COMSOL Multiphysics, позволяющая смоделировать и симулировать физические процессы [6, с. 277].
Определение модели
Геометрия многослойной композитной оболочки состоит из шести плоских слоев Н-образной формы, уложенных друг на друга. Высота секции составляет 25 см, толщина полотна – 15 см, ширина фланца – 25 см, толщина фланца – 5 см. Геометрия многослойной композитной оболочки показана на рис. 1.

Рис. 1. Геометрия многослойной композитной оболочки
Последовательность укладки
Каждый слой композитной оболочки имеет толщину 0,125 мм, как показано на рис. 3. Композитная оболочка имеет [30/-45/75/-75/45/-30] последовательность укладки, как показано на рис. 2. Эта последовательность укладки является антисимметричной по отношению к средней плоскости композитной оболочки.
Трехмерное представление геометрии, а также первое основное направление материала, показывающее ориентацию волокон в каждом слое физической геометрии, показаны на рис. 4 и 5 соответственно.
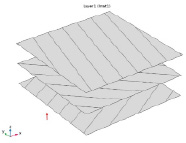
Рис. 2. Последовательность укладки [30/-45/75/-75/45/30], показана ориентация волокон в каждом слое снизу вверх
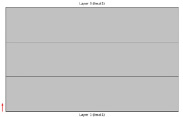
Рис. 3. Вид многослойной композитной оболочки по толщине, показывающий толщину (0,125 мм) каждого слоя
Свойства материала
Все слои многослойной композитной оболочки изготовлены из углеродных волокон в эпоксидной смоле. Свойства гомогенизированного ортотропного эластичного материала (матрица упругости) приведены в табл. 1. В ней представлены только ненулевые элементы матрицы эластичности.
Таблица 1
Матрица эластичности композитного материала
|
Матрица эластичности |
Значение |
|
{D11, D12, D13, D22, D23, D33, D44, D55, D66} |
{141.34, 3.35, 3.35, 10.25, 2.83, 10.25, 4.52, 2.95, 4.52} |
Гомогенизированные ортотропные тепловые свойства многослойной композитной оболочки приведены в табл. 2.
Таблица 2
Теплопроводность многослойной композитной оболочки
|
Теплопроводность |
Значение (Вт/(м·К)) |
|
{k11, k22, k33} |
{6.2, 0.5, 0.5} |
Поскольку анализ является стационарным, значения плотности и теплоемкости при постоянном давлении для многослойной композитной оболочки не влияют на результаты и устанавливаются равными единице. Все упругие и термические свойства материала задаются в системе координат многослойной композитной оболочки (локальные направления материала слоя), где первая ось совпадает с ориентацией волокна.
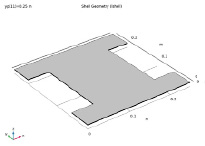
Рис. 4. Трехмерное геометрическое изображение многослойной композитной оболочки
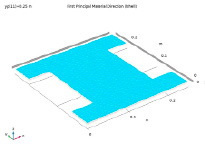
Рис. 5. Первое основное направление материала, показывающее ориентацию волокон в каждом слое физической геометрии. Угол наклона слоя используется в качестве цвета для каждого слоя
Коэффициент теплового расширения
Гомогенизированное значение коэффициента теплового расширения ламината для заданных свойств волокна и матричного материала рассчитываются с использованием правила смешивания. Свойства составляющих материалов, необходимые для определения коэффициента теплового расширения ламината, приведены в табл. 3.
Исходя из свойств материала, приведенных в табл. 3, коэффициенты теплового расширения для ламината в направлении волокон, а также перпендикулярно направлению волокон рассчитываются по правилу смешивания по формулам 1-3.
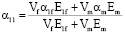 , (1)
, (1)
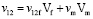 , (2)
, (2)
Таблица 3
Свойства углеродного волокна и эпоксидной смолы
|
Свойства материала |
Значение |
Описание |
|
Vf |
0,6 |
Объемная доля волокна |
|
Vm |
0,4 |
Объемная доля матрицы |
|
E1f |
230[GPa] |
Модуль Юнга волокна в направлении волокна |
|
Em |
4[GPa] |
Модуль Юнга матрицы |
|
ν12f |
0,2 |
Коэффициент Пуассона волокна |
|
νm |
0,35 |
Матричный коэффициент Пуассона |
|
α1f |
-0,6E-6[1/K] |
Коэффициент теплового расширения волокна в направлении волокна |
|
α2f |
8,5E-6[1/K] |
Коэффициент теплового расширения волокна перпендикулярно направлению волокна |
|
αm |
55E-6[1/K] |
Коэффициент теплового расширения матрицы |
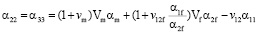 . (3)
. (3)
Значения коэффициентов теплового расширения слоев композитной оболочки, рассчитанные с использованием этих выражений, приведены в табл. 4. Коэффициент теплового расширения в направлении волокон на три порядка меньше, чем коэффициент, перпендикулярный направлению волокна. Это связано с тем, что углеродные волокна имеют отрицательный коэффициент теплового расширения в направлении волокон.
Таблица 4
Коэффициенты теплового расширения слоев композитной оболочки
|
Коэффициент теплового расширения |
Value (1/K) |
|
{α11, α22, α33} |
{3,72E-8, 3,47E-5, 3,47E-5} |
Граничные условия и нагрузки
К модели применяются следующие граничные условия и нагрузки:
− Конструктивные граничные условия: Края при X = 0 и X = 25 см фиксированы.
− Тепловые граничные условия. Температура установлена на комнатную температуру по краям при X = 0 и X = 25 см. Конвективный тепловой поток с коэффициентом теплопередачи 20 Вт/(м2·К) наносится на нижнюю поверхность многослойной композитной оболочки (внешнюю границу раздела нижнего слоя).
− Тепловые нагрузки: На верхнюю поверхность многослойной композитной оболочки (внешнюю границу раздела верхнего слоя) наносится луч мощностью 10 Вт. Положения источника луча по оси x и z фиксируются в пространстве на расстоянии 12,5 см и 25 см, в то время как y-образное положение балки варьируется от 0 до 25 см. Стандартное отклонение балки принимается равным 1/10 от ее высоты (или z-положения), что составляет 2,5 см.
Результаты исследования и их обсуждение
Температурный профиль в композитной оболочке, когда источник теплового излучения находится над ее центром, показан на рис. 6. Максимальная температура наблюдается только в центре оболочки и распределяется по всем направлениям от центра. Распределение температуры также можно проверить, создав линейные графики вдоль осей X и Y, как показано на модели.
Влияние ортотропии материала и ориентации слоев проявляется в характере тепловых напряжений и деформаций, как показано на рис. 7. Общий характер тепловых напряжений аналогичен температурному профилю, показанному на рис. 6, поскольку оболочка подвергается только тепловым нагрузкам. Однако можно наблюдать интересную картину деформации, вызванную ортотропией и ориентацией слоев.
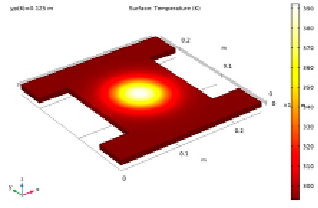
Рис. 6. Температурный профиль при yp = 12,5 см
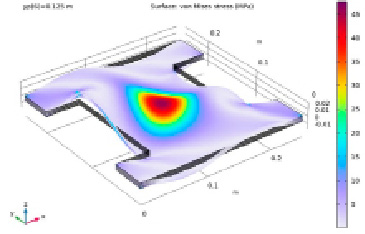
Рис. 7. Распределение напряжений фон Мизеса в многослойной композитной оболочке при y-положении балки (yp) = 0,125 м
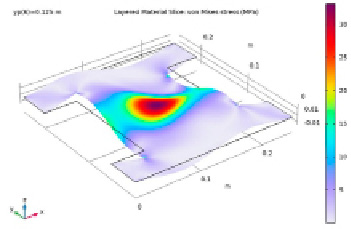
Рис. 8. Распределение напряжений фон Мизеса в средней плоскости многослойной композитной оболочки при положении балки (yp) = 0,125 м
Чтобы увидеть влияние ориентации слоев на распределение напряжений по фон Мизесу, в средней плоскости многослойной композитной оболочки создается график слоистого среза материала, как показано на рис. 8. Можно видеть, что он имеет другое распределение напряжений, а также величину по сравнению с рис. 7, на котором показано распределение напряжений для верхнего слоя.
На рис. 9 показано изменение напряжения фон Мизеса по толщине в четырех различных местах оболочки. Неравномерность напряжения по слоям видна на графике. Существует вращательная симметрия напряжений между точками, расположенными между ними.
На рис. 10–13 показаны распределения напряжений фон Мизеса и различных компонентов тензора напряжений в системе координат слоистого материала. Напряжения нанесены на график в средней плоскости каждого слоя. Эффект антисимметричной укладки хорошо виден на рис. 10–12. Например, распределение напряжений в слое 1 и в слое 6 аналогично, но антисимметрично относительно средней плоскости многослойного композитного материала.
На рис. 13 показано распределение напряжения сдвига, а также антисимметричный рисунок. Знак напряжения меняется на противоположный при сравнении верхнего и нижнего слоев из-за антисимметрии.
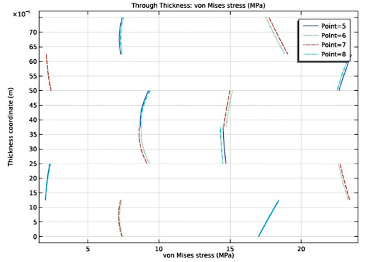
Рис. 9. Изменение напряжения фон Мизеса по толщине в выбранных точках при yp = 0,125 м
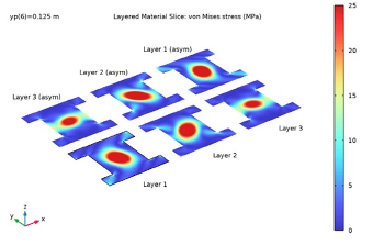
Рис. 10. Напряжение фон Мизеса в системе координат ламината в средней плоскости каждого слоя при yp = 0,125 м
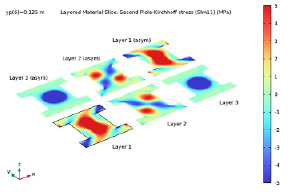
Рис. 11. Составляющая напряжения 11 (направление волокон) в средней плоскости каждого слоя при yp = 0,125 м
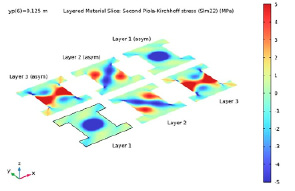
Рис. 12. Составляющая напряжения 22 (поперечная направлению волокон) в средней плоскости каждого слоя при yp = 0,125 м
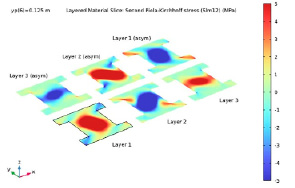
Рис. 13. Составляющая напряжения 12 (сдвиг в плоскости) в средней плоскости каждого слоя при yp = 0,125 м
Выводы
1. Проведен расчет коэффициента теплопроводности на основе правила смешивания перпендикулярно направленных базальтовых волокон и матрицы.
2. Введены и рассмотрены свойства материала углеродного волокна и эпоксидной смолы, а также общие параметры пластины, теплопередачи и луча в программе компьютерного моделирования. Установлено, что коэффициент теплового расширения в направлении волокна на три порядка меньше, чем коэффициент, перпендикулярный направлению волокна.
3. Зафиксировано, что максимальная температура наблюдается, когда источник теплового излучения находится над центром оболочки, и она распределяется по всем направлениям, удаленным от центра. Посредством компьютерной программы продемонстрировано, что на распределение температуры также влияет направление позиции луча и толщина пластины.
4. Влияние ортотропии материала и ориентации слоев проявляется в характере тепловых напряжений и деформаций.



