Аналитическое решение контактной задачи существует лишь для простейших случаев контакта двух деформируемых тел [1]. В общем случае конструкционных контактных задач (терминология Г.Б. Иосилевича) необходимо использовать дискретные численные методы (при этом наиболее сложные задачи – случаи зацепления зубьев зубчатых передач).

При контактном взаимодействии двух деформируемых тел должны выполняться условия совместности перемещений точек, контактирующих на их поверхностях, под действием нагрузки [2; 3]. Это условие можно описать в виде интегрального уравнения:

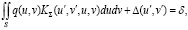(1)

где s – площадь контакта взаимодействующих тел; q – контактное напряжение (давление); u,v – текущие координаты точки приложения силы; u',v' – текущие координаты точки измерения перемещений поверхностей тел; KΣ (u',v',u,v) – функция влияния распределённых нагрузок на сумму перемещений поверхностей тел вследствие всех деформаций взаимодействующих тел; Δ – зазор между поверхностями взаимодействующих тел до нагружения; δ – сближение контактирующих тел, являющееся мерой их деформирования.

Кроме условия совместности перемещений, должны выполняться и условия равновесия сил [2; 3], которые можно описать интегральным уравнением:

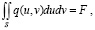(2)

где F – внешняя сжимающая сила.

Путём решения системы уравнений (1) и (2) можно найти, как распределяется нагрузка по площадкам контакта. Для возможности получения такого решения при неизвестных заранее размерах, форме и числе площадок контакта между взаимодействующими телами эта система уравнений должна быть дополнена краевыми (граничными) условиями:

для всех точек на площадках контакта

q > 0, Δ+W = δ, (3)

на свободных (вне площадок контакта) поверхностях тел

q = 0, Δ+W > δ, (4)

где W – сумма всех видов деформаций поверхностей тел под действием нагрузки; δ – сближение контактирующих тел, являющееся мерой их деформирования.

Дискретный численный итерационный метод решения прямой (при заданной величине внешней сжимающей силы F ) контактной задачи был предложен К.И. Заблонским. Система интегральных уравнений (1) и (2) сводится к системе (n + 1) линейных алгебраических уравнений. Так как размеры площадок контакта и число n участков, передающих нагрузку, заранее неизвестны, распределение нагрузки находится методом итераций, когда система линейных уравнений решается много раз, с последовательным исключением участков, на которых нагрузка принимает отрицательные значения, и уточнением границ площадок контакта в ходе итераций. Недостатки этого метода: 1) необходимо много раз (на каждой итерации внешнего цикла) находить решение систем линейных алгебраических уравнений (СЛАУ) большой размерности; 2) такой подход можно использовать только в линейной постановке задачи деформативности.

Дискретный численный метод решения обратной (при заданном сближении δ контактирующих тел) контактной задачи был предложен Г.И. Шевелевой. Недостатки этого метода: 1) в проектном расчете (при заданной величине внешних сил) необходимо неоднократно (при нелинейной зависимости δ(Fn) не менее 3 раз) тратить вычислительные ресурсы и память ЭВМ на трудоёмкое решение прямой контактной задачи; 2) приходится аппроксимировать нелинейную зависимость δ(Fn), что вносит дополнительные погрешности в расчёт, для уменьшения которых приходится вводить дополнительные промежуточные точки аппроксимации, т.е. дополнительно тратить вычислительные ресурсы ЭВМ на дополнительные решения обратной контактной задачи; 3) учёт только контактных деформаций в подходе Г.И. Шевелевой.

Направления исследований: разработка систем компьютерного и имитационного моделирования, алгоритмов и методов имитационного моделирования на основе анализа математических моделей.

Предметная область: системы компьютерного и имитационного моделирования.

Объект исследования – алгоритмы и методы имитационного моделирования на основе анализа математических моделей.

Цель исследования – разработать дискретный численный итерационный алгоритм и метод имитационного моделирования прямой конструкционной контактной задачи на основе анализа математических моделей, лишённый указанных выше недостатков существующих методов К.И. Заблонского и Г.И. Шевелевой, для последующего использования нового алгоритма и метода в разработке систем компьютерного и имитационного моделирования.

Материалы и методы исследования

Для решения дискретным методом [4] разобьём площадку контакта, лежащую в общей касательной плоскости контактирующих поверхностей тел, на прямоугольные участки, в пределах которых контактная нагрузка будет считаться равномерно распределенной и равной её значению в центре каждого участка. Условия совместности перемещений должны будут выполняться в расчётных точках, расположенных в центрах участков. При этом решение контактной задачи сводится к решению алгебраической системы уравнений:

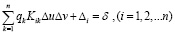
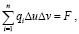(5)

где i – номер контактирующего участка; n – число таких участков; qi , qk – контактные напряжения (давления) на участках; Kik – коэффициент влияния единичной, равномерно распределённой по k-му участку нагрузки на сумму перемещений поверхностей зубьев (вследствие деформаций зубьев и их оснований) в расчётной точке i-го участка; Δu, Δv – длина и ширина прямоугольных участков; Δi – зазор до нагружения (в направлении общей контактной нормали) между поверхностями тел в расчётной точке i-го участка.

Без учета сил трения и при линейном поступательном перемещении при сближении деформируемых тел систему (5) можно представить в виде:

Δi+Wi = δ, (i=1,…,n);

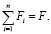(6)

Для вывода основной итерационной формулы нового итерационного алгоритма второе уравнение системы уравнений (6) разделим почленно на величину δ:

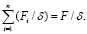(7)

Учитывая, что из первого уравнения непосредственно имеем δ=Δi+Wi, заменим этой суммой величину δ в левой части выражения (7) и получим:

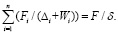(8)

Дробное выражение в левой части (8) обозначим как:

fi = Fi /(Δi +Wi), (i = 1,..,n). (9)

Эта величина fi , удовлетворяющая условию равновесия сил, и будет использоваться для уточнения значения величины Fi (сумма сил, равномерно распределенных по i-му участку) (i = 1,..,n), на каждой последующей итерации внутреннего цикла. Окончательно получаем следующий вид итерационной формулы:

Fi ,k+1 = fi F /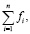 (10)

где Fi,k+1 – новое значение силы Fi,k, уточнённое для следующей итерации; k – порядковый номер итерации; fi – величина, обеспечивающая выполнение условий совместности перемещений в ходе итерационного процесса, полученное выше выражение для неё имеет вид:

fi = Fi,k /(Δi +Wi), (i = 1,..,n). (11)

Докажем, что выражение (10) обеспечивает обязательное выполнение условия равновесия сил на каждой итерации внутреннего цикла. При использовании выражения (10) имеем:

= =

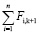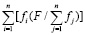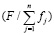
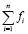= =F.

Следовательно, 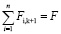, что и требовалось доказать.

Итерационная формула (10) используется в итерациях внутреннего цикла для уточнения величины, равнодействующей на i-м участке силы Fi. В итерациях внешнего цикла по условиям (3) и (4) производится уточнение границ площадок контакта и числа n участков, передающих нагрузку. За величину δ линейного сближения деформируемых тел при этом можно принимать или максимальное из величин δi (i=1,…,n), полученных в конце каждого внутреннего цикла итераций, или их среднее значение.

Для обоснования сходимости итерационного алгоритма выразим из (10) отношение

Fi,k+1 / Fi,k =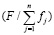 / (Δi +Wi). (12)

Предположим, что величина δ = const. Тогда из (7) имеем, что

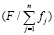= δ. (13)

Если Δi+Wi < δ, то из (13) с учётом (14) имеем Fi,k+1 > Fi,k .

Если Δi+Wi = δ, имеем Fi,k+1 = Fi,k .

Если Δi+Wi > δ, имеем Fi,k+1 < Fi,k .

Это доказывает, что при δ = const предлагаемый итерационный алгоритм всегда сходится. Результаты расчётов на ЭВМ показали, что описанный итерационный алгоритм сходится также и при монотонно убывающем, монотонно возрастающем или асимптотическом изменении величины δ в ходе итераций.

Тестовая проверка

Тестовая проверка работы нового дискретного численного итерационного алгоритма и метода имитационного моделирования прямой конструкционной контактной задачи проводилась для классической задачи контакта сферы с упругой полуплоскостью [1].

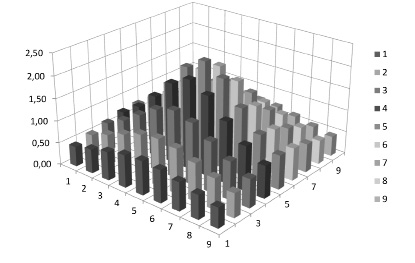
Рис. 1. Итерация 1

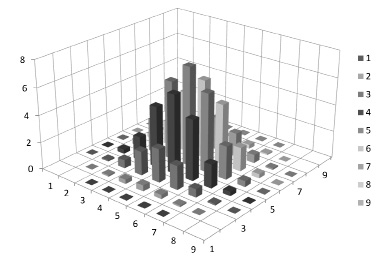
Рис. 2. Итерация 8

На рис. 1–3 приведены изменения эпюр напряжений в ходе итераций (неблагоприятный случай начального распределения нагрузки – равномерное при ).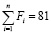

На рисунке 4 приведён наглядный график сходимости итерационного процесса по изменению величины невязки перемещений Ei.

В результате новым итерационным методом всего за 18 итераций получено решение с полуэллиптической эпюрой напряжений, аналогичное классическому решению Г. Герца [1].

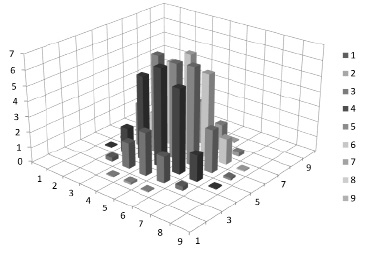
Рис. 3. Итерация 18 (последняя)

Рис. 4. График сходимости итерационного процесса

Практическое использование

Сравнение результатов моделирования разработанным дискретным численным итерационным алгоритмом и методом с экспериментальными данными А.С. Яковлева и В.И. Печеного [5] (единственный эксперимент с прямым (не косвенным) определением величины контактных давлений (напряжений) для зубьев передач с локальным контактом) приведено на рис. 5. При моделировании учитывались контактные и изгибно-сдвиговые деформации.

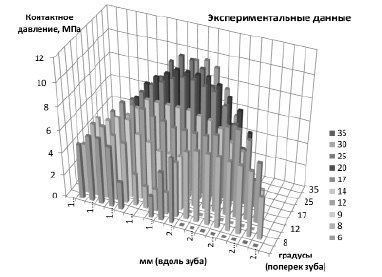
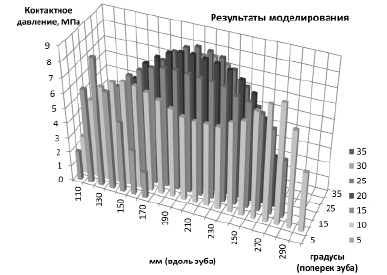
Рис. 5. Данные эксперимента [5] и результаты моделирования

Использованный дискретный численный итерационный алгоритм и метод не имеет недостатков метода К.И. Заблонского (многократное решение систем линейных уравнений большой размерности, учёт только линейной зависимости деформаций от сил) и метода Г.И. Шевелевой (решение только обратной задачи при заданном сближении δ контактирующих тел, учёт только контактных деформаций).

Также практическое использование разработанного дискретного численного итерационного алгоритма и метода было при имитационном моделировании распределения контактных давлений (напряжений) по площадкам контакта в цилиндрических зубчатых передачах Новикова (в том числе с учётом погрешностей изготовления и сборки) и в модифицированных глобоидных передачах.

Заключение

Разработанный дискретный численный итерационный алгоритм и метод можно применять при нелинейной зависимости деформаций от сил. В ходе вычислений не требуется многократно решать систему линейных алгебраических уравнений высокого порядка (пока не определились границы площадок контакта и число контактирующих дискретных участков, нет необходимости в точном решении). Всё это экономит вычислительные ресурсы и память ЭВМ. Поэтому при использовании предложенного дискретного численного итерационного алгоритма и метода можно повысить точность решения конструкционных контактных задач и скорость работы систем компьютерного и имитационного моделирования.

Разработанный дискретный численный итерационный алгоритм и метод имитационного моделирования прямой конструкционной контактной задачи на основе анализа математических моделей в дальнейшем будет использоваться для последующей разработки систем компьютерного и имитационного моделирования.