Отказы в автоматизированных системах возникают под воздействием разнообразных факторов и являются случайными событиями.
Из существующего опыта наиболее часто встречающимися законами распределения при оценке показателей надежности узлов автоматизированных систем являются экспоненциальное распределение, распределение Вейбулла и нормальное распределение.
Экспоненциальное распределение является типичным для сложных объектов, состоящих из многих элементов с различным распределением наработки. Также отметим, что в автоматизированных системах поток отказов каждого узла формируется из суммы потоков отказов его составных элементов [1].
Однако в некоторых случаях необходимо оценить показатели надежности отдельных узлов и элементов автоматизированной системы, например привода дверей пассажирских вагонов. Этот расчет даст возможность скорректировать состав ЗИП и оптимизировать плановое техническое обслуживание системы. Работа элементов и узлов системы может быть описана различными распределениями. Рассмотрим более подробно нормальное распределение при оценке показателей надежности.
Нормальное распределение случайной величины возникает тогда, когда на эту величину воздействует большое число однородных по своему влиянию случайных факторов, при этом влияние каждого из этих факторов по сравнению с совокупностью всех остальных является незначительным [2, с. 38]. Если перенести это условие на отказы технических систем, то нормальный закон достаточно точно описывает работы изделий на этапе старения и износа [3].
Нормальное распределение характеризуется двумя параметрами μ и σ, которые численно равны математическому ожиданию и среднему квадратическому отклонению. Следует учесть, что на практике находит применение усеченный нормальный закон распределения, так как величина времени не может быть отрицательной.
В [4; 5] систематизирована информация по применению нормального закона распределения в надежности, которая опубликована в отечественной и зарубежной литературе, представлены зависимости, позволяющие провести оценивание основных показателей надежности.
Однако до сих пор в литературе отсутствуют методические рекомендации проведения расчета надежности технических систем по нормальному закону распределения согласно реальным данным из эксплуатации.
Цель исследования – рассмотреть процесс оценки наработки до отказа элементов автоматизированных систем на базе нормального закона распределения по данным из эксплуатации и сформировать ряд практических рекомендации для проведения расчета.
Материалы и методы исследования
В общем случае порядок оценки надежности по данным из эксплуатации можно отобразить следующей схемой (рис. 1).
Рассмотрим оценку параметра наработки до отказа на примере элементов и узлов автоматических наружных дверей пассажирских вагонов (рис. 2). Двери наружные для пассажирских вагонов обеспечивают вход в вагон и выход из вагона наружу, защиту тамбура вагона от воздействия климатических внешних воздействующих факторов и предотвращают несанкционированный доступ внутрь вагона [6].
Согласно [7, с. 5] наработка до отказа – это наработка объекта от начала его эксплуатации или момента его восстановления до отказа. Исходя из определения данный показатель надежности может быть использован как для восстанавливаемых, так и для невосстанавливаемых систем.
В качестве объекта исследований определим приводной ремень. Основной тип отказа – обрыв. Изделие невосстанавливаемое, поэтому рассмотрим оценку параметра наработки до отказа по данным из эксплуатации.
На первом этапе определим объем испытаний. Для оценки показателя средней наработки до отказа принимаем план испытаний NUz. Согласно [8, с. 13] для нормального распределения объем необходимой выборочной совокупности объекта (N) определяется по формуле
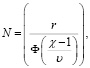(1)
где r – прогнозируемое число отказов;
χ – относительная продолжительность испытаний;
υ – коэффициент вариации.
Предположим, что доверительная вероятность составляет q = 0,9, относительная ошибка ɛ = 0,1, а коэффициент вариации υ = 0,3. Тогда согласно [8, с. 15] для показателя «средняя наработка до отказа» прогнозируемое число отказов будет составлять r = 16.
Произведем оценку относительной продолжительности испытаний согласно формуле
χ = Ти / Тср , (2)
где Ти – продолжительность испытаний в сутках,
Тср – заданная в технических условиях требуемая наработка до отказа.
Допустим, что согласно технической документации имеем Тср = 18000 ч (не менее 750 суток).
Продолжительность испытаний определим из выражения
Ти = Tг ∙ KТИ , (3)
где Tг – количество дней наблюдений;
KТИ – коэффициент технического использования пассажирских вагонов.
Рассмотрим расчет приводных ремней за год. Подставим численные значения в (3) и получим
Ти = 365 ∙ 0,85 ≈ 310 суток.
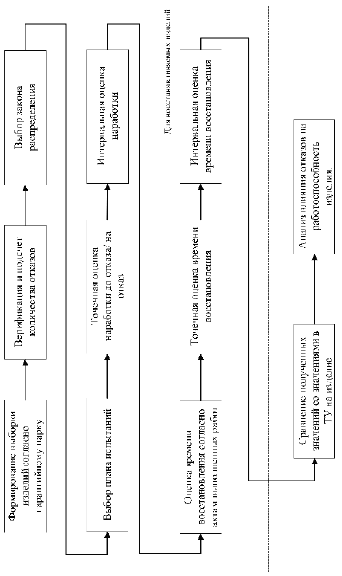
Рис. 1. Порядок расчета показателей надежности в эксплуатации
Рис. 2. Элементы дверей пассажирского поезда, работу которых можно описать нормальным законом распределения
Следует отметить, что некоторые компоненты вагонов могут также иметь свой среднегодовой коэффициент технического использования (например, система отопления). Тогда выражение (3) перепишется как
Ти = Tг ∙ KТИ ∙ KТИЭ ,
где KТИЭ – коэффициент технического использования элемента или компонента вагона.
Подставляя в формулу (2) числовые значения, получаем
χ = 310 / 750 = 0,41.
Значение Φ определяем из таблицы значений функции стандартного нормального распределения. Для удобства можно воспользоваться средствами MS Excel, применив функцию НОРМСТРАСП(z). Подставляя в (1) числовые значения, получим
шт.
Исходными данными для определения наработки до отказа являются данные по отказам, которые получены по результатам эксплуатации за год.
Далее обозначим выборку пассажирских вагонов. Предположим, что имеется 300 ед. Тогда фактическое количество приводных ремней составит 1200 шт. (в учет возьмем только автоматические двери вагона – две торцевые и две боковые двери рабочего тамбура). Таким образом, условие о необходимом минимальном объеме выборочной совокупности приводных ремней выполняется:
Nф = 1200 > N = 610.
Определим суммарную наработку приводных ремней, которые установлены на боковые и торцевые двери пассажирских вагонов исследуемой выборки, за назначенный период наблюдения.
,
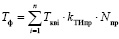где Tквi – суммарная календарная наработка i-го пассажирского вагона за время наблюдения, сутки;
kТИпр – коэффициент технического использования приводных ремней (принимается равным коэффициенту технического использования вагонов);
Nпр – общее количество приводных ременей, установленных на автоматические двери вагона.
Разобьем наработку на две части – наработка отказавших приводных ремней и наработка работоспособных приводных ремней. Предположим, что в первом случае это 1000 суток, а во втором – 80 000 суток.
Тогда фактическая наработка отказавших приводных ремней составит
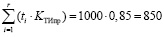суток,
где ti – наработка i-го приводного ремня до отказа.
Фактическая наработка приводных ремней, не имеющих отказы, будет составлять
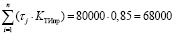суток,
где τj – наработка j-го приводного ремня до цензурирования.
Таким образом получаем суммарную фактическую наработку:
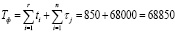суток.
Перейдем непосредственно к оценке средней наработки до отказа.
Точечная оценка средней наработки до отказа (μ) вычисляется в соответствии с [8, с. 73]:
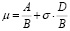, (4)
где
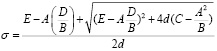(5)
– оценка среднеквадратического отклонения нормального распределения.
В (5) A, B, C, D, E – вспомогательные промежуточные параметры, которые рассчитываются следующим образом:
,
,
,
,
,
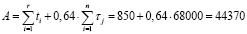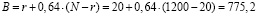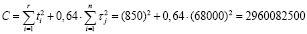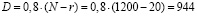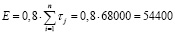где N – суммарное количество приводных ремней на вагонах, Nф = 1200 шт.;
d = r – число отказов наблюдаемых приводных ремней из выборки вагонов за рассматриваемый период. Определим d = 20.
Подставим числовые значения в (5) и получим
суток.
Далее осуществим точечную оценку средней наработки до отказа по формуле (4) и получим
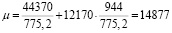суток, или μч = 14877 ∙ 24 = 357048 часов.
Произведем оценку наработки до отказа по нижней доверительной границе согласно формуле
μн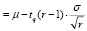
, (6)
где tq(r – 1) – квантиль распределения Стьюдента;
r – число отказов.
По таблице 72 [8, с. 115] tq(r – 1) при r = 20 составляет 1,3253.
Подставляя числовые значения в формулу (6), получим
μн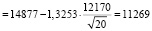
суток
или μнч = 11269 ∙ 24 = 270456 часов.
Результаты исследования и их обсуждение
Таким образом, получаем, что для наблюдаемой совокупности приводных ремней автоматических дверей средняя наработка до отказа по нижней доверительной границе составляет µнч = 270456 ч, что больше, чем установлено в технической документации на изделие (Тср = 18000 ч).
По итогам расчета наработки до отказа происходит анализ полученных значений, формируется ряд действий в проектной и эксплуатирующей организациях:
1. Пересмотр протокола по анализу видов и последствий отказов (АВПО/FMEA) [9]. По итогам «мозгового штурма» группы инженеров происходит перерасчет приоритетного числа риска (ПЧР) и при необходимости вносятся изменения в конструкцию или технологический процесс.
2. При необходимости производится поиск нового поставщика элемента системы или улучшаются его качественные характеристики на базе предприятия-изготовителя.
3. Оптимизируется состав и количество ЗИП. Если рассматривать конкретный пример, то эта оптимизация должна быть проведена в депо и на вагоноремонтных заводах.
4. Внедрение RCM-систем (Reliability centered maintence) на производстве для предупреждения отказов, что обеспечит эффективный уровень требуемой безопасности, готовности и экономичной эксплуатации изделия [10].
Заключение
В статье рассмотрен алгоритм расчета показателей надежности элемента автоматической двери пассажирского поезда. Представленный численный пример разъясняет методологию оценки наработки до отказа приводного ремня двери как невосстанавливаемого элемента системы. Также даны рекомендации, которые будут полезны при анализе эксплуатационной надежности сложных технических систем.