Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Вопрос о проведении косметического ремонта помещений рано или поздно встает перед каждым человеком и организацией, обладающей недвижимым имуществом. Состояние внутренней отделки в процессе эксплуатации здания со временем ухудшается ввиду различных причин, например случайного физического повреждения. В этом случае встает вопрос о целесообразности проведения косметического ремонта. Однако однозначно ответить на этот вопрос нельзя, ведь на принятие решения могут повлиять различные факторы и ограничения, которые к тому же могут варьироваться от владельца помещений к владельцу. При одной совокупности факторов и ограничений принимается положительное решение о начале выполнения ремонтных работ, при другой – предложение о проведении ремонта отклоняется.

Сейчас такое решение принимается в «ручном режиме»: уполномоченный человек должен осмотреть помещения, ознакомиться с имеющейся информацией и документацией, принять во внимание налагаемые ограничения, например максимально допустимую стоимость работ, спрогнозировать примерный срок выполнения ремонта и, основываясь на проведенном анализе имеющихся данных, принять решение. Это затратно с точки зрения времени и денежных ресурсов, которые идут на оплату труда специалиста. В идеале данный процесс должен быть автоматизирован, что позволит оптимизировать работу предприятий, работающих в сфере косметических ремонтов.

В современном мире существует тенденция к внедрению информационных технологий во многие процессы, включая принятие решений в различных сферах, например в области менеджмента [1] и в экономике [2]. Однако данная тенденция, к сожалению, обошла стороной процесс принятия решения о проведении косметического ремонта помещений. Можно возразить, что все-таки существуют такие исследования, например [3-6], но стоит отметить, что данные научные работы затрагивают тему капитальных ремонтов, а не косметических. Соответственно область, связанная с косметическими ремонтами помещений недвижимого имущества, на текущий момент не обладает результатами научных работ и требует решения данной проблемы. Одним из первых шагов в реализации данного решения является создание математической модели, которая будет имитировать процесс принятия решения о проведении косметического ремонта помещения. Разработка данной математической модели позволит опираться на нее в будущих исследованиях, связанных с косметическими ремонтами помещений, которые впоследствии приведут к автоматизации данной сферы.

Целью данной работы является формирование математической модели процесса принятия решения о проведении косметического ремонта помещения с учетом имеющихся факторов и налагаемых ограничений.

Материалы и методы исследования

Прежде всего, стоит установить конечное множество ответов, из которых система будет извлекать самый релевантный в конкретной ситуации с учетом имеющихся факторов и ограничений. Для данной задачи – принимать решение о проведении косметического ремонта – будет достаточной четкая логика, которая допускает существование только двух ответов – «Истина» и «Ложь», «Да» и «Нет», «Следует проводить ремонт» и «Не следует проводить ремонт». Использование нечеткой логики, которая расширяет множество ответов до трех и более, не имеет смысла, поскольку системе стоит дать четкий ответ о необходимости проведения косметического ремонта без какой-либо неопределенности.

Исходя из того, что у системы есть только два варианта ответа, математическая модель должна выдавать результат из двух возможных значений. Но так как результат математической функции число, а результат модели представляет собой ответ из конечного множества элементов «Да» и «Нет», необходимо наличие порога, который будет приводить результат к одному из ответов. Будем называть такой порог границей смены решения. Условимся, что ответу «Да» соответствует 1, а ответу «Нет» – 0. Общий вид такой математической модели выглядит следующим образом:

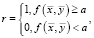(1)

где r – результат работы системы; f(x,y) – функция учета факторов и ограничений; x – вектор факторов размерностью n; y – вектор ограничений размерностью ≤ n; a – граница смены решения.

Компактнее записать модель (1) можно с помощью скобки Айверсона, тогда она примет следующий вид:

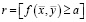. (2)

Записав математическую модель в общем виде, необходимо раскрыть функцию учета влияющих на принятие решения факторов и ограничений.

Каждый фактор должен обладать своим коэффициентом, иначе говоря, весом, который показывает степень влияния фактора на результат. На основе этого очевидным решением будет вести учет факторов с помощью взвешенной средней арифметической, которая подразумевает под собой наличие весовых коэффициентов у слагаемых, т.к. оценивается совокупное влияние факторов на принятие решения. Другие средние не подойдут по следующим причинам: средняя геометрическая отображает темпы роста; средняя гармоническая применяется при неизвестных весовых коэффициентах. Таким образом, функция учета факторов и ограничений приобретает следующий вид:

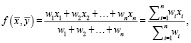(3)

где f(x,y) – функция учета факторов и ограничений; x – вектор факторов размерностью n; y – вектор ограничений размерностью ≤ n; wi – вес i-го фактора; xi – i-й фактор.

При этом факторы, на которые накладываются ограничения, должны учитывать эти самые ограничения. Реализовать это можно с помощью разницы между единицей и отношением значения фактора к значению ограничения. В таком случае превышение фактором ограничения даст отрицательную величину, которая будет смещать результат в сторону ниже границы смены решения. Однако в таком случае при превышении ограничений может сложиться ситуация, когда модель выдает решение о проведении косметического ремонта. Такое поведение модели допускается для того, чтобы можно было пренебречь незначительным превышением ограничения при условии, что все остальные факторы говорят о необходимости выполнения косметического ремонта. Тогда формула (3) примет вид:

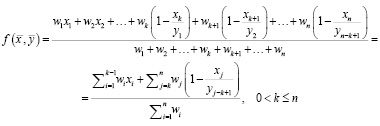, (4)

где f(x,y) – функция учета факторов и ограничений; x – вектор факторов размерностью n; y – вектор ограничений размерностью n – k + 1; wi – вес i-го фактора; xi – i-й фактор; yi – i-е ограничение.

Очевидно, что в результате функции (4) могут получаться разные числа, чтобы было удобнее обрабатывать результат, эти числа следует нормализовать. Однако для нормализации необходимо знать минимальное и максимальное возможные значения функции, которые в данном случае являются –∞ и +∞ соответственно. Это следует как минимум из того, что хоть факторы и ограничения в действительности не могут быть бесконечными (например, бюджет), теоретически данные параметры модели не ограниченны. Исходя из этого, нормализовать выход функции не представляется возможным.

Таким образом, математическая модель (2) приобретает вид:

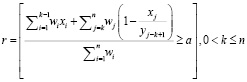, (5)

где r – результат работы математической модели системы; wi – вес i-го фактора; xi – i-й фактор; yi – i-е ограничение; a – граница смены решения.

Дальнейшая часть статьи касается частного случая, т.к. в математическую модель могут быть введены различные дополнительные факторы и ограничения, влияющие на процесс принятия решения о проведении косметического ремонта. Данное изменение множества факторов и ограничений приведет к необходимости переопределения весовых коэффициентов.

Факторы представляют собой независящие от человека обстоятельства, которые влияют на принимаемое решение, ограничения – накладываемые человеком условия, которым должны удовлетворять факторы. Для определения весовых коэффициентов факторов необходимо предварительно установить, какие факторы и ограничения будут учитываться в модели. Далее приведен список ограничений и факторов, влияющих на принятие решения о проведении косметического ремонта помещения.

Количество дефектов внутренней отделки одного вида. Большое количество дефектов одного вида будет склонять систему к решению о проведении косметического ремонта, при этом отсутствие дефектов конкретного вида не будет влиять на принятие решения.

Площадь дефектов одного вида. Дефектов может быть много, однако пораженная площадь может быть небольшой (скопление мелких трещин в месте единоразового физического приложения силы к стене), и наоборот (одна трещина может разрастись на всю стену), и это стоит учитывать при принятии решения.

Т.к. количество и площадь дефектов одного вида относятся к одному и тому же смысловому объекту – дефекту, то имеет смысл учитывать их совместно в виде произведения. Что касается веса, то предлагается установить для всех видов дефектов одно и то же значение, чтобы каждый вид имел одинаковый вклад в принятие решения.

Бюджет. Данный пункт представляет собой ограничение, в которое должен уложиться по стоимости планируемый ремонт. Т.е. бюджет допускает расходы ниже или равные конкретному числу.

Стоимость выполнения ремонта. Данный фактор представляет собой совокупность всех сопутствующих ремонту трат. Сюда включаются стоимость материалов, стоимость отдельных видов работ и т.д.

Прогнозируемое время ремонта. Немаловажным моментом является знание предположительной продолжительности ремонтных работ. Допустим, что такой показатель уже имеется, т.к. его определение – тема отдельного исследования.

Требуемое время ремонта. Ограничение, которое накладывается на прогнозируемое время ремонта. Аналогично бюджету, ограничиваемый фактор должен быть ниже или равен конкретному числу.

Прогнозируемое изменение стоимости материалов. Стоимость материалов имеет свойство изменяться по различным причинам, например перепроизводство, сезон проведения строительных и ремонтных работ. Поэтому немаловажным фактором является ее изменение. Условимся, что такой показатель также уже известен.

Квалификация ремонтной бригады. Оценить профессиональный уровень ремонтной бригады можно в виде произведения стажа бригады на разницу между количеством успешных и проваленных ремонтных проектов. Очевидно, что такое вычисление данного фактора не совсем корректно ввиду того, что состав бригады может меняться, и это никаким образом не учитывается, однако для демонстрации примера определения весовых коэффициентов разработанной математической модели это приемлемо.

Оценка старости используемых материалов. На принятие решения о проведении косметического ремонта влияет степень старости используемых материалов, т.к. более старую отделку имеет смысл заменить, не дожидаясь возникновения большого количества дефектов. Имеет смысл оценивать данный показатель в виде числа на промежутке [–1,1], где оценка –1 означает новые материалы, срок эксплуатации которых только начался, а 1 – материалы, срок эксплуатации которых закончился. Соответственно, число 0 означает материал на середине своего срока эксплуатации. Также можно оценивать данный параметр на промежутке [0,1], чтобы новые материалы не склоняли модель к отказу от выполнения косметического ремонта, но в данной работе рассматривался именно первый вариант промежутка.

На текущем этапе необходимо определить веса факторов, влияющих на принятие решения и границу смены решения в математической модели (5). Эта задача весьма нетривиальна, учитывая, что веса и граница должны соотноситься друг с другом, чтобы математическая модель выдавала релевантный результат. Для этого необходимо выбрать один параметр, веса либо границу, и зафиксировать, чтобы была возможность регулировать второй параметр относительно первого. Исходя из этого возникают два возможных варианта решения этой проблемы. Первый вариант – установить веса для каждого фактора, зафиксировать их и выполнять работу по поиску оптимальной границы смены решения. Второй вариант – выбрать конкретную границу смены решения и регулировать веса математической модели. Первый подход требует скрупулезного выбора весов модели, при том что сложность выбора будет возрастать с количеством факторов. Второй подход не обладает данными сложностями ввиду того, что регулирование весов происходит относительно одной конкретной величины. Далее будет описан вариант с регулированием весов математической модели относительно границы смены решения.

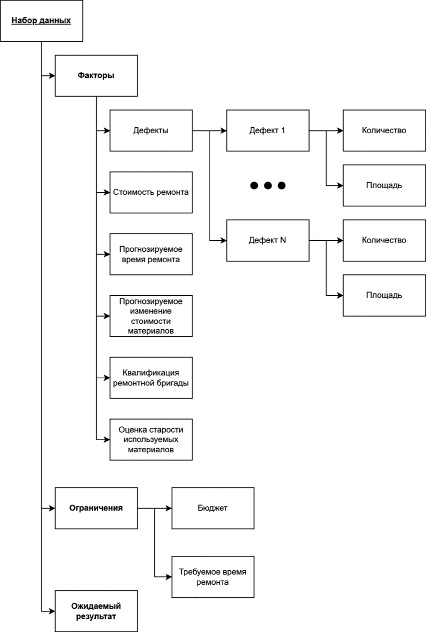
Рис. 1. Структура тренировочного и проверочного наборов данных

Для определения оптимальных весов на языке программирования Python 3.9.4 был реализован генетический алгоритм. Генетические алгоритмы опираются на принципы эволюции в природе с имитацией естественного отбора и случайных мутаций решений задач [7].

Для определения весов генетическому алгоритму необходимы исходные данные в виде факторов, ограничений и ожидаемого результата, на которые алгоритм опирается при формировании весов. В данном исследовании имелось 10 тренировочных и 5 проверочных наборов данных, представленных в формате JSON. Такой небольшой объем данных объясняется тем, что перед данной частью исследования ставилась задача продемонстрировать возможность определения весов математической модели принятия решения о проведении косметического ремонта таким способом. На тренировочных данных генетический алгоритм пытался подобрать оптимальные веса, которые впоследствии тестировались на проверочных данных. Наборы данных представляют собой совокупность факторов, ограничений и ожидаемый результат. Структура таких данных представлена на рисунке 1. Наборы тренировочных и проверочных данных были получены у профильного эксперта.

Как было сказано ранее, генетический алгоритм имитирует процесс эволюции, в ходе которого получается наилучшее решение, в рамках данной статьи – набор наилучших весовых коэффициентов. Алгоритм симулировал скрещивание нескольких решений, вследствие чего образовывались новые последовательности весов, приспособленность которых оценивалась в виде количества принятых решений, соответствующих ожидаемым из наборов данных (чем выше приспособленность, тем наиболее удачные оказались веса и тем лучше принимает решения математическая модель).

Генетический алгоритм запускался для нескольких границ смены решения, которые составляют значения в промежутке от 5 до 45 включительно с шагом 5. Также исследовались две ситуации с нижними границами весов: –10 и 0, верхняя граница значений весов всегда оставалась равной 10. Для каждой комбинации «граница смены решения / нижняя граница весов» генетический алгоритм выполнялся по 1000 раз для сбора статистических данных. В задаче рассматривались следующие веса: вес дефекта, вес соответствия бюджету, вес изменения стоимости материалов, вес соответствия требуемому времени, вес квалификации ремонтной бригады, вес степени старости используемого материала. В «популяции» присутствовало 50 особей-коэффициентов. За максимальное количество «популяций» было взято число 15 000. Значение вероятности «мутаций», т.е. случайным образом изменение случайного веса на любое ненулевое значение в допустимых пределах, было установлено 0,3. Для создания новой «популяции» решений применялся метод отбора усечением с границей 0,4. За точку останова была взята ситуация, когда все принятые решения соответствуют ожидаемым либо количество «популяций» достигло определенного числа. Далее в таблице 1 приведены вышеперечисленные параметры, которые были заданы генетическому алгоритму.

Таблица 1

Значения параметров генетического алгоритма для поиска оптимальных весов математической модели принятия решения о проведении косметического ремонта помещения

По итогам выполнения генетического алгоритма при всех изменяемых параметрах и тестировании весовых коэффициентов в математической модели на проверочной выборке были получены статистические данные, на основе которых были построены гистограмма максимальных значений приспособленности (представлена на рисунке 2) и графики изменения среднего значения приспособленности и результатов тестирования при изменении нижней границы весов и границы смены решения (представлены на рисунках 3 и 4). Графики и гистограмма будут проанализированы в следующем разделе.

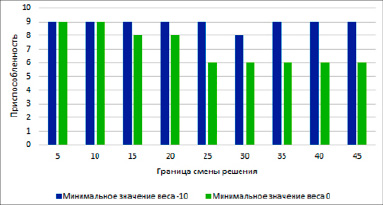
Рис. 2. Гистограмма максимальных значений приспособленности

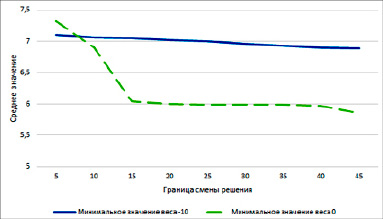
Рис. 3. Изменение среднего арифметического приспособленности

Таблица 2

Один из лучших наборов весовых коэффициентов математической модели при границе смены решения, равной 5, полученный с помощью генетического алгоритма

Исходя из представленных выше графиков и гистограммы, для получения весовых коэффициентов математической модели (5) генетический алгоритм был настроен следующим образом: за границу смены решения было принято значение, равное 5, а в качестве возможного минимального значения веса было взято число –10. Далее в таблице 2 представлен один из лучших полученных наборов весов математической модели (5) при рассмотренных выше факторах.

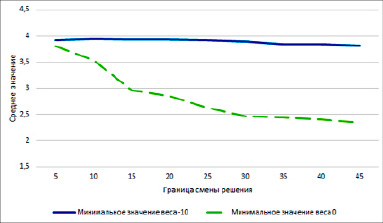
Рис. 4. Изменение среднего арифметического результатов тестирования

Таблица 3

Сводная таблица с результатами применения математической модели при границе смены решения, равной 5

Стоит отметить, что при добавлении новых факторов либо ограничений в математическую модель весовые коэффициенты следует переопределить.

В таблице 3 представлены результаты применения математической модели (5) при использовании весовых коэффициентов, приведенных в таблице 2, и при границе смены решения, равной 5, на некоторых проверочных наборах данных.

Результаты исследования и их обсуждение

Полученная математическая модель (5) позволяет имитировать процесс принятия решения о проведении косметического ремонта помещения. Также стоит отметить, что т.к. в модели учитываются только факторы и ограничения, то можно использовать данную модель для принятия аналогичного решения для всего здания в целом, а не только применительно к помещениям. Необходимо только лишь определить факторы, привести их к количественному виду и установить необходимые ограничения.

Стоит обратить внимание, что может сложиться ситуация, когда значение фактора равно значению накладываемого ограничения, в таком случае весовой коэффициент будет умножаться на ноль и никакого влияния на принимаемое решение этот фактор не будет оказывать. Может показаться, что это недостаток модели, однако все вполне логично – при небольшом превышении ограничения сразу же получится отрицательное число, которое будет смещать результат ниже границы смены решения, и наоборот – при небольшой положительной разнице между ограничением и фактором будет положительно число. Ноль же обозначает полное соответствие значения фактора значению ограничения, а, следовательно, отсутствие экономии в факторе не влияет на решение.

Гистограмма, представленная на рисунке 2, демонстрирует, что при значении возможного минимального весового коэффициента равного –10, т.е. с возможными отрицательными весами, генетический алгоритм вполне способен сформировать весовые коэффициенты, которые позволят математической модели выдавать наиболее релевантные результаты. Объясняется это тем, что генетическому алгоритму в этой ситуации проще варьировать попадание результата в определенную часть числовой прямой относительно границы смены решения. Согласно гистограмме, при минимальном допустимом значении весового коэффициента, равном 0, при увеличении границы смены решения генетический алгоритм не может выдавать таких же весовых коэффициентов, обеспечивающих релевантную работу математической модели.

Средние арифметические на графиках (рис. 3 и 4) отображают тенденцию (направление графика) и скорость (крутизна графика) изменения приспособленности весовых коэффициентов при увеличении значения границы смены решения. Так, при значении возможного минимального весового коэффициента, равного –10, графики демонстрируют стабильно высокие показатели, в то время как если веса ограничиваются неотрицательными числами, наблюдается резкое ухудшение показателей приспособленности. Данное поведение может отличаться от того, которое будет проявляться при изменении верхней границы значения весового коэффициента, однако данная ситуация не рассматривалась в данном исследовании.

Схожее поведение графиков средней приспособленности (рис. 3) и средних результатов тестирования (рис. 4) позволяет утверждать, что полученные статистические данные корректны.

В качестве границы смены решения следует использовать число 5, т.к. результаты на графиках, пусть хоть более или менее стабильны при наличии отрицательных весов, но все же имеется некоторое их ухудшение с увеличением значения границы смены решения.

Проведенный выше анализ позволяет настроить генетический алгоритм таким образом, чтобы он выдавал наилучшие весовые коэффициенты для предложенной в статье математической модели.

Представленные ранее в таблице 2 весовые коэффициенты применимы только при рассмотренных в статье факторах и ограничениях и требуют их переопределения при изменении множеств факторов и ограничений. Также стоит отметить, что это не единственные весовые коэффициенты, которые дают наилучшие результаты в рассмотренном случае.

Результаты работы математической модели, представленные в таблице 3, демонстрируют, что математическая модель (5) выполняет поставленную перед ней функцию – она моделирует процесс принятия решения о проведении косметического ремонта, основываясь на имеющихся факторах и ограничениях. Однако полученный результат при втором наборе проверочных данных демонстрирует, что математическая модель допустила ошибку из-за небольшого пересечения границы смены решения. Решение данной ошибки является предметом дальнейших исследований.

Заключение

В данной работе была представлена математическая модель процесса принятия решения о проведении косметического ремонта помещения. Данную математическую модель можно использовать для имитации процесса принятия решения о проведении косметического ремонта помещения. Также на нее можно опираться при разработке системы автоматического принятия решения о проведении косметического ремонта помещения.

С помощью эвристического подхода в виде генетического алгоритма были получены веса математической модели. Аналогичным образом можно переопределить весовые коэффициенты при изменении множеств факторов и ограничений, влияющих на принимаемое решение.

Проведен анализ полученных результатов, позволяющий настраивать генетический алгоритм таким образом, чтобы он выдавал наилучшие весовые коэффициенты для предложенной в статье математической модели.

Представлены результаты применения разработанной математической модели на некоторых проверочных данных, что демонстрирует работоспособность данной модели.