Изучение динамики транспортных и пешеходных потоков, прогнозирование их характеристик необходимо при формировании и оптимизации транспортной инфраструктуры городов. Информация о распределении транспортных потоков по улично-дорожной сети важна для управления дорожным движением, в частности с помощью интеллектуальных транспортных систем. Основную нагрузку на элементы улично-дорожной сети составляют регулярные по времени потоки транспортных средств между парами районов отправлений – прибытий, информация о которых хранится в матрице корреспонденций. С этой точки зрения актуальной задачей представляется разработка методов определения и динамического обновления матрицы корреспонденций при введении новых потокообразующих элементов, в частности методов сбора и обработки необходимой информации о потоках, методов идентификации параметров транспортных и пешеходных потоков.
Оценка статической матрицы корреспонденций достаточно хорошо изучена. Обычно используется предварительная матрица для получения единственного решения. В целом эти методы могут быть классифицированы следующим образом [1]:
− метод наименьших квадратов (Cascetta E., Nguyen S., 1988; Doblas J., Benitez F.G., 2005) и обобщенный метод наименьших квадратов (Bell M.G.H., 1991; Nie Y.M., Zhang H.M., 2010; Caggiani L., 2013). Как правило, эти методы представляют собой двухуровневые задачи. Верхний уровень должен минимизировать отклонение между наблюдаемым и расчетным количеством трафика за все временные интервалы, а также отклонение между целевым или установленным спросом и расчетными матрицами корреспонденций. Модель нижнего уровня решает статическую задачу пользовательского равновесия;
− методы, основанные на концепции энтропии (например, Van Zuylen H.J., Willumsen L., 1980; Xie C., Kockelman K.M., Waller S.T., 2011). Эти методы максимизируют энтропию с учетом набора ограничений. Концепция энтропии измеряет, насколько более точно отражает реальную ситуацию текущая матрица корреспонденций по сравнению с предшествующей;
− методы максимального правдоподобия (например, Spiess H., 1987; Parry M., Hazelton M.L., 2012). В этом случае предполагается, что элементы исходной матрицы корреспонденций получены из набора случайных величин с заданным распределением вероятностей;
− Байесовские методы (например, Maher M.J., 1983; Perrakis K., Karlis D., Cools M., Janssens D., Vanhoof K., Wets G., 2012; Wei C., Asakura Y., 2013; Castillo E., Menéndez J.M., 2008; Cheng L., Zhu S., Chu Z., Chen J., 2014), которые используют наблюдаемые подсчеты трафика для обновления предполагаемого априорного распределения, апостериорное распределение всех переменных строится на основе теоремы Байеса. Эти методы рассматривают поток трафика как случайную величину.
Оценка зависящего от времени спроса на корреспонденции гораздо сложнее случая статического. Некоторые исследователи прямо распространяют методы статической оценки матрицы корреспонденций на динамический случай с использованием изменяющихся во времени подсчетов данных (например, Cascetta E., Inaudi D., Marquis G., 1993; Tavan H., Mahmassani H.S., 2001; Bierlaire M., Crittin F., 2004).
Однако, несмотря на большое количество исследований [2, 3], изучение методов составления и обновления матрицы корреспонденций остается актуальной задачей, так как в связи с развитием новых технологий появляются новые возможности по сбору данных. Кроме того, для разных моделей транспортной сети и разных транспортных задач требуются различные исходные данные, а также приемлемы различные методы обновления или получения информации.
Целью данной работы является разработка вероятностно-статистических методов планирования наблюдений для оценки обновления данных о корреспонденциях, вызванных новым слоем спроса.
Материалы и методы исследования
Матрица корреспонденций (OD-матрица) содержит информацию о числе транспортных средств, проходящих от «источника» (места отправления) к «стоку» (месту прибытия) в течение времени t . Матрицу пропорциональных отношений (link proportions), определяющую часть трафика на каждой из дуг, относящихся к определенной паре «источник – сток», обозначают как LP-матрицу. Ранее [4] автором был разработан и обоснован метод определения динамической матрицы корреспонденций, построенной с учетом исходных данных, требующихся для расчетов с помощью авторской модели TIMeR_Mod [5]. Модель основана на оценке маршрутов транспортных потоков: устанавливается зависимость между элементами матрицы корреспонденций и стоимостью движения по маршруту. Основная идея заключается в том, чтобы использовать стоимость движения по маршрутам (функцию транспортных затрат) для установления пользовательского равновесия. Для динамического обновления матрицы корреспонденций применяется фильтр Кальмана. С помощью OD-матрицы и LP-матрицы корректируется распределение интенсивности по дугам транспортной сети, которая в авторской модели TIMeR_Mod содержится в матрицах ASTREETS и BINTERSECTION [5].
В данной работе ставится задача планирования эксперимента для обновления данных о распределении транспортных потоков при введении новых пунктов притяжения корреспонденций, то есть в случае появления нового слоя спроса.
Одной из основных проблем является проблема идентификации, связанная с построением математических моделей динамических систем по экспериментальным данным. Ее качественному решению способствует применение на практике математических методов и новых технологий. Суть вероятностно-статистических методов принятия решений состоит в использовании вероятностных моделей на основе оценивания и проверки гипотез с помощью выборочных характеристик. На практике вероятностные и статистические методы обычно применяются в том случае, когда выводы, основанные на выборочных данных, переносятся на всю совокупность [6]. Однако при этом в каждой конкретной ситуации следует предварительно оценить принципиальную возможность получения достаточно достоверных вероятностных и статистических данных.
В данной работе рассматривается задача обновления данных об OD-матрице при появлении нового пункта притяжения корреспонденций. Задача о распределении транспортных потоков предполагает два основных этапа. На первом этапе на основе исходных данных о потокообразующих факторах строится одна или несколько матриц корреспонденций населения, которые определяют ограничения на общий объем передвижений в сети между источниками и стоками движения. Второй этап предполагает равновесное распределение транспортных потоков согласно первому принципу Вардропа.
Существуют физические и технологические ограничения при наблюдении за транспортной сетью. Реализация отдельных моделей может быть очень затратной. Поэтому при планировании эксперимента следует учитывать вышеуказанные ограничения [7].
Современные технологии позволяют использовать различные типы датчиков для сбора данных о транспортных потоках. Сюда можно отнести GPS, видео, автоматическую идентификацию транспортных средств, сканирование номерных знаков и т.д. По типу собираемых датчиками данных их можно разделить на несколько категорий [1]:
− датчики, подсчитывающие количество транспортных средств по полосам дорожной сети (I категория);
− видеодатчики, которые могут снимать видеоизображения движущихся потоков (II категория);
− идентификаторы транспортного средства, с помощью которых можно получать различные данные о трафике, включая маршрут, задержки на перекрестках, время в пути или по отдельным отрезкам пути (III категория).
Синтезировать данные от всех типов источников для оценки корреспонденций позволяет Байесовский метод. Кроме того, доказано, что данный метод хорошо аппроксимирует наблюдаемые данные [1–3].
В данной статье рассматриваются вероятностно-статистические методы планирования наблюдений для оценки обновления данных о корреспонденциях, вызванных новым слоем спроса, не останавливаясь на их физической реализации.
Результаты исследования и их обсуждение
1. Планирование эксперимента для оценивания матрицы корреспонденций
Для оценивания интенсивности движения по полосам транспортной сети, что может использоваться в Байесовском методе как априорная информация для получения оценок, необходимо выбрать узлы транспортной сети (вершины графа – в модели транспортной сети) для установки датчиков I или II категории. В силу ограниченности ресурсов невозможно установить датчики во всех узлах. Поэтому надо выбрать наиболее информативные. В этом случае обратимся к вероятностно-статистическим методам.
Степень неопределенности системы определяется числом ее состояний и вероятностями пребывания в этих состояниях. Характеристикой априорной вероятности системы является ее энтропия.
Энтропией системы [8] называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей с противоположным знаком:
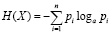, (1)
где a > 0, a ≠ 1
Или, учитывая определение математического ожидания,
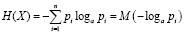. (2)
Энтропия сложной системы (X, Y ) равна
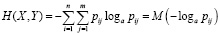. (3)
Условная энтропия системы Y при условии X = xi:
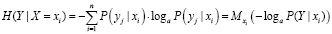. (4)
Средняя или полная энтропия системы Y в зависимости от того, какие состояния принимает система Х:
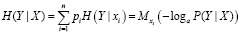. (5)
Если системы X и Y зависимы, то
H(X, Y) = H(X) + H(Y | X). (6)
Если рассмотреть случай независимости систем, то
H(X, Y) = H(X) + H(Y). (7)
Другой крайний случай – состояние системы Х полностью определяет состояние системы Y. Тогда H(Y | X) = 0, а энтропия системы равна
H(X, Y) = H(X). (8)
Количество информации IX измеряется уменьшением энтропии системы, для уточнения которой предназначены сведения. Количество информации, необходимое для полного выяснения состояния системы: IX = H(X).
Поставим задачу определения оптимального расположения точек наблюдения при составлении или уточнении матрицы корреспонденции с учетом новых пунктов притяжения. Абстрактный транспортный граф – это совокупность вершин (перекрестков, узлов сети) и ребер (часть улично-дорожной сети между соседними перекрестками).
Пусть K – новый пункт притяжения (новый сток заявок), а Di, i = 1,2,…,k – возможные источники заявок. Требуется определить наиболее информативные вершины для расположения наблюдателей при условии ограниченных ресурсов, то есть возможность установить не более N0 наблюдателей.
Пусть определены вершины графа, через которые может проходить маршрут. Их количество равно N. Априори произвольная заявка может пройти с равной вероятностью через любую из этих вершин на пути в K, то есть вероятность пребывания в вершине X = xi равна, pi = 1 / N, i = 1,2,…,N. В этом случае (для слоя {D}i ↔ K) можем считать, что состояние системы X {вся улично-дорожная сеть} полностью определяет система Y.
Пусть имеется mi направлений, по которым можно продолжить движение от вершины X = xi, причем только si из них могут привести в пункт K (si < mi). Найдем количество информации о системе, которую можно получить отдельно от каждого из состояний X = xi.
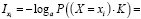
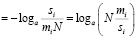. (9)
Заметим, что (mi / si) > 1, логарифм – монотонно возрастающая функция при a > 0, a ≠ 1. Поэтому больше информации несет тот узел сети, из которого выходит больше дуг, ведущих в пункт K.
Предлагается следующий алгоритм для определения оптимального расположения точек наблюдения при уточнении матрицы корреспонденции для слоя {D}i ↔ K:
1) определяем маршруты как перечень вершин графа, ведущие от каждого из источников Di, i = 1,2,…,m к стоку – пункту K;
2) включаем все вершины из пункта 1) алгоритма в множество X = {xi | i = 1,2,…,N};
3) определяем количество mi направлений, по которым можно продолжить движение от вершины X = xi, количество si тех из них, которые могут привести в пункт K (si < mi);
4) найдем количество информации:
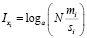, i = 1,2,…,N;
5) упорядочим по убыванию величины Ixi , выберем N0 из них.
Так как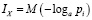 
, то это обеспечит наибольшую информативность.
Следующая задача: оценить необходимое число измерений, которые следует произвести в каждой вершине, чтобы с заданной надежностью получить параметры распределения транспортного потока.
Рассмотрим оценку вероятности выбрать определенное направление из положения X = xi.
В схеме испытаний случайная величина X принимает значение 1 («успех») с вероятностью p и значение 0 («неудача») с вероятностью (1−p), оптимальной несмещенной оценкой p является относительная частота успешных исходов в n испытаниях:
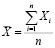. (10)
Cтатистика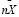 
имеет биномиальное распределение [9]. Выборочная средняя – асимптотически нормальная величина, у которой 
.
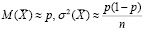Тогда можно оценить при уровне значимости α (надежности 1 – α) построить асимптотический доверительный интервал:
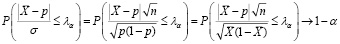, где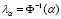 
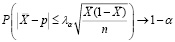. (11)
Следовательно, ошибка при замене вероятности относительной частотой при заданной надежности 1 – α равна
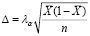. (12)
Если требуется, чтобы ошибка не превзошла r % от оценки, то следует решить неравенство
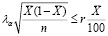. (13)
Решив, получим оценку количества опытов для получения необходимой точности оценки:
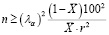. (14)
2. Оценивание матрицы корреспонденций
Найдем оценку условной вероятности P*(K | Di) того, что заявка из пункта Di выедет в пункт K, с помощью Байесовского подхода [8, 9].
Пусть имеется выборка из распределения Бернулли с параметром p: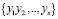 
, полученная с помощью III категории датчиков.
И пусть про параметр p возможно предположить, будто любые его значения априори одинаково вероятны. Тогда
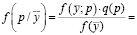
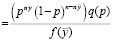(15)
– условная плотность распределения,
где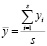 
.
Заметим, что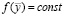 
, а также в силу предположения о равновозможности вероятностей p: 
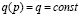. Данная плотность является плотностью бета-распределения 
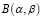c параметрами 
:
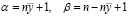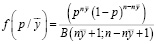. (16)
Математическое ожидание бета-функции равно
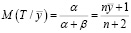. (17)
То есть примем
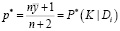. (18)
Обозначим Di , i = 1,2,…,k – оценки общего объема заявок в одноименных пунктах Di.
Тогда по формуле Байеса доля заявок, прибывших в пункт K, при условии, что пунктом отправления был Di:
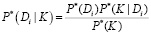, (19)
где
,
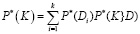а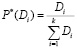 
. (20)
При известном предполагаемом объеме прибытий NK заявок/час в пункте K (возможно получить с помощью датчиков I и II категории), найдем оценку количества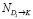 
заявок/час, отбывающих из пункта Di:
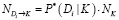. (21)
Таким образом оцениваются корреспонденции слоев спроса {D}i ↔ K.
Если предварительно известны вероятности предпочтения одного из возможных маршрутов из каждого пункта Di, то остается перераспределить объемы корреспонденций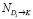 
, пропорционально увеличив интенсивности по соответствующим дугам. Данные об интенсивностях по дугам транспортной сети снимаются в вершинах, отобранных согласно алгоритму в пункте 1. Результат перераспределения объема корреспонденций по улично-дорожной сети в авторской модели TIMeR_Mod отражается в матрицах ASTREETS и BINTERSECTION.
Заключение
В работе с помощью вероятностно-статистических методов решается задача оптимального планирования эксперимента с целью наблюдения за транспортными потоками на улично-дорожной сети в случае, когда требуется оценить изменение транспортных корреспонденций. Разработан алгоритм для определения оптимального расположения точек наблюдения при оценивании изменений в матрице корреспонденций, вызванных появлением нового слоя спроса {D}i ↔ K. Кроме того, уделено внимание определению количества экспериментов, необходимых для достижения требуемой точности расчетов.
Результаты исследования имеют практическую значимость, так как позволяют оптимизировать временные и трудовые ресурсы при решении задачи обновления матрицы корреспонденций в случае введения в эксплуатацию новых объектов на улично-дорожной сети.