Адаптивные алгоритмы принятия решений находят широкое применение в современной науке, технике, в управлении технологическими процессами и производствами. Единого определения адаптивных алгоритмов не существует, поэтому на практике его заменяют многочисленными понятиями [1, с. 67]. В данном случае под адаптивным алгоритмом будем понимать такой алгоритм принятия решения [2, с. 33], при реализации которого используется предварительный анализ информации об исследуемом объекте с последующим получением оценок о его состоянии. Применение адаптивных алгоритмов в информационно-измерительных системах (ИИС) [3, с. 53] позволяет при решении ряда задач, связанных с количественной оценкой физических величин, повысить правильность принятия решения о количестве измеряемых или контролируемых характеристик за счет повышения адекватности принимаемой модели информационного процесса реальному процессу, и является одной из важных задач, стоящих перед разработчиками и производителями ИИС. Применение адаптивных алгоритмов в ИИС можно отнести к одному из направлений искусственного интеллекта, широко востребованному в настоящее время. В предлагаемой статье рассматривается возможность применения разработанного автором адаптивного алгоритма принятия решения в конкретной ИИС измерения основных точностных показателей механических часов.
Целью исследования является разработка и реализация адаптивного алгоритма принятия решения для обоснованного подхода к выбору необходимого набора показателей точности наручных механических часов, подлежащих измерению и контролю с помощью ИИС, позволяющего автоматизировать технологический процесс их измерения и контроля.
Материалы и методы исследования
В настоящее время для оценки точностных показателей средств измерений (СИ) используется достаточно большое количество метрологических характеристик (МХ) [4]. Известно, что МХ СИ – это характеристики, влияющие на погрешность результата измерениия. Для каждого вида СИ в нормативно-технической документации указываются свои особености измерения физических величин и соответствующие им наборы МХ. Однако количество МХ СИ в ряде случаев без какого-либо научного обоснования устанавливается принудительно в соответствующих стандартах. Достаточно большое количество МХ, указанных в стандартах, приводит к усложнению и удорожанию технологического процесса измерения и контроля. Поэтому одной из актуальных задач современных ИИС является установление набора показателей точности различных видов СИ, минимально необходимых для описания их метрологических свойств с заданной степенью достоверности.
Автором решается конкретная задача выбора и измерения научно обоснованного набора МХ наручных механических часов с применением адаптивного алгоритма принятия решения, что является научной новизной данной работы.
Существующие подходы выбора системы показателей точности для наручных механических часов, основанные на применении соответствующих стандартов, не позволяют оценить качество механических часов по точностным показателям с заданной степенью достоверности. Это связано с тем, что процесс накопления погрешности измерения времени в наручных механических часах носит нестационарный характер и получаемые оценки МХ зависят от времени и изменяются по случайному закону. Более удобные, независимые от времени числовые оценки, описывающие процесс накопления погрешности в механических часах, достаточно сложно пока получить на основе теории нестационарных процессов. Поэтому требуемую систему числовых оценок точностных показателей механических часов возможно получить при применении специальных классов нестационарных процессов, которые могут служить статистической моделью процесса накопления погрешности в наручных механических часах. В качестве объекта исследования в данной работе рассматриваются наручные механические часы для измерения времени, относящиеся к техническим средствам хронометрии (ТСХ). Особенность часов (механических, кварцевых, электронных) состоит в том, что, являясь средствами измерения времени (интервалов времени), они сами выступают в качестве объектов измерения, и измерению подвергаются их МХ. Анализ процессов эволюции МХ механических наручных часов, проведенный автором, подтверждает, что среди указанных процессов наиболее близкими для описания процесса накопления погрешности являются случайные (нестационарные) процессы со стационарными приращениями (СПСП) [5, с. 79]. Теоретический и экспериментальный анализ статистической динамики ТСХ [6, с. 21] подтверждает достаточную эффективность такой идентификации, что позволяет принять ее в качестве основной модели процесса накопления погрешности наручных механических часов.
Рассмотрим возможность применения такой модели на основе анализа погрешности измерения времени (интервалов времени) наручных механических часов с последующей реализацией полученных результатов в ИИС. Погрешность измерения интервалов времени является важнейшей МХ часов и представляет собой разность между отсчетами времени ti и истинным значением (эталонный интервал времени) ti0 в момент времени ti.
∆ti = ti.– ti0. (1)
Погрешность измерения времени в механических часах и погрешность генератора, формирующего эталонные интервалы времени, не остаются постоянными и накапливаются во времени по некоторому случайному закону. Погрешность механических часов обусловлена погрешностью измерения времени. Анализ погрешности наручных механических часов показывает, что накопление погрешности является нестационарным случайным процессом [5, с. 81; 6, с. 21], а формулы для оценки математического ожидания и дисперсии этого процесса можно записать в виде полиномов [6, с. 30]:
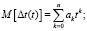(2)
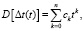
где ∆t(t) – погрешность измерения интервалов времени ТСХ;
ak, ck – постоянные величины.
Формула (2) показывает, что для описания погрешности измерения времени механическими часами необходимо знать значения всех коэффициентов [5, с. 82]. Поскольку накопление погрешности носит характер нестационарного случайного процесса, то автором для описания этого процесса применен специальный вид случайного нестационарного процесса со стационарными приращениями (СПСП). В этом случае выражение (2) заменяется приближенными оценками на основе процессов вида СПСП [6, с. 31]. И процесс накопления погрешности в часах, с учетом этих допущений, может быть записан в виде
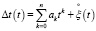, (3)
где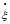 
– центрированный случайный стационарный процесс.
С учетом выражения (2) можно записать выражение (3) в виде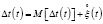 
.
Следовательно, общая информационная модель процесса накопления погрешности в механических часах может быть представлена в виде [6, с. 2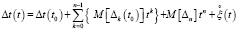4]:
, (4)
где ∆t(t0) – начальное значение погрешности.
Результаты исследования и их обсуждение
Информационная модель процесса накопления погрешности, представленная формулой (4), позволяет оценить характер накопления погрешности и на ее основе получить частные информационные модели накопления погрешности в наручных механических часах. Частные информационные модели будут зависеть от стационарности соответствующих приращений погрешности измерения времени часами. Так, если стационарными являются первые приращения погрешности, для которых выполняются условия
M[∆1(t)] = M[∆1], (5)
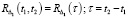, (6)
где M[∆1(t)] – математическое ожидание первого приращения;
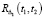– корреляционная функция первого приращения;
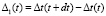– приращение погрешности за достаточно малое время dt,
то получим первую частную модель процесса накопления погрешности, определяемую выражениями
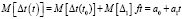, (7)
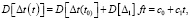(8)
где f – номинальная частота колебаний осциллятора часового механизма часов, определяющая дискретность отсчетов времени. Представленная частная модель процесса накопления погрешности определяется коэффициентами a0, a1, c0, c1, где a0 и c0 – аддитивные составляющие, не изменяющиеся во времени [5, с. 81].
В качестве примера рассмотрим расчет коэффициента a1 для механических наручных часов. Основой расчета послужили статистические испытания наручных механических часов отечественного производства, проведенные автором и описанные им в монографии [6, с. 25]. При начальных значениях
M1[∆1] = 2 мкс, M2[∆1] = 4 мкс, M3[∆1] = 6 мкс,
M4[∆1] = 8 мкс, M5[∆1] = 10 мкс и f = 2,5 Гц,
коэффициенты a1 будут принимать соответственно значения
a11 = 0,5∙10-5, a12 = 1,0∙10-5, a13 = 1,5∙10-5,
a14 = 2,0∙10-5 и a15 = 2,5∙10-5.
Графики процессов накопления погрешности M[∆t(t)], при условии стационарности первых приращений [7, с. 58] и расчитанных значениях коэффициента a1 и a0 = 0, представлены на рис. 1.
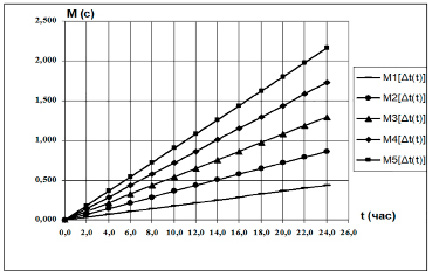
Рис. 1. Графики зависимости M[∆t(t)]
Аналогично рассчитываются и строятся графики дисперсии процессов накопления погрешности D[∆t(t)] [5, с. 84].
Если стационарными являются вторые приращения погрешности, для которых выполняются условия
M[∆2(t)] = M[∆2], (9)
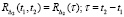, (10)
где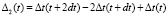 
, то получим вторую частную модель процесса накопления погрешности, определяемую выражениями (9) и (10).
Определим математическое ожидание и дисперсию для второй частной математической модели процесса накопления погрешности, определяемую выражениями
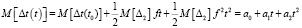, (11)
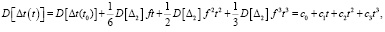(12)
где a0, a1, a2, c0, c1, c2, c3 – коэффициенты второй частной модели процесса накопления погрешности в часах.
Также рассмотрим пример расчета коэффициентов a1 и a2 для механических наручных часов [6, с. 26]. При тех же начальных значениях, что и для первой модели, коэффициент a1 будет принимать соответственно значения:
a11 = 0,25∙10-5, a12 = 0,5∙10-5, a13 = 0,75∙10-5, a14 = 1,0∙10-5 и a15 = 1,25∙10-5,
а коэффициент a2 будет принимать соответственно значения:
a21 = 6,25∙10-5, a22 = 12,5∙10-5, a23 = 18,75∙10-5, a24 = 25∙10-5, a25 = 31,25∙10-5.
Графики процессов накопления погрешности M[∆t(t)], при рассчитанных значениях коэффициентов a1 и a2 и при a0 = 0, показаны на рис. 2. Аналогично рассчитываются и строятся графики дисперсии процессов накопления погрешности D[∆t(t)].
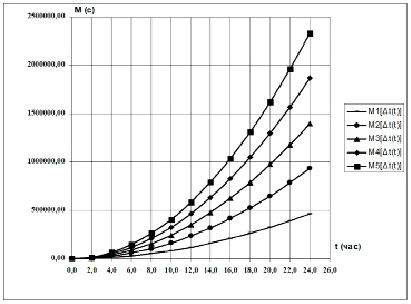
Рис. 2. Графики зависимости M[∆t(t)]
Третья частная модель накопления погрешности определяется стационарностью третьих приращений, которые можно записать в виде выражений
M[∆3(t)] = M[∆3], (13)
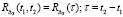, (14)
где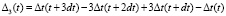 
.
Математическое ожидание и дисперсия для третьей частной модели определяются формулами
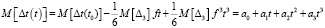, (15)
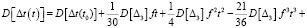
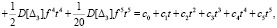(16)
где a0, a1, a2, a3, c0, c1, c2, c3, c4, c5 – коэффициенты третьей частной модели процесса накопления погрешности в часах. Примером расчета коэффициентов a1, a2, a3 для механических наручных часов послужили статистические испытания наручных механических часов, проведенные автором и описанные в его монографии [6, с. 27], при тех же начальных значениях, что и для первой модели. Коэффициент a1 будет принимать соответственно значения:
a11 = 0,083∙10-5, a12 = 0,16∙10-5, a13 = 0,25∙10-5, a14 = 0,33∙10-5 и a15 = 0,42∙10-5,
коэффициент a2 = 0, коэффициент a3 будет принимать соответственно значения:
a31 = 0,052∙10-5, a32 = 0,104∙10-5, a33 = 0,156∙10-5, a34 = 0,2∙10-5, a35 = 0,26∙10-5.
Графики процессов накопления погрешности M[∆t(t)] при рассчитанных значениях коэффициента a1 и a3, также при a0 = 0 , a2 = 0 приведены на рис. 3. Аналогично рассчитываются и строятся графики дисперсии процессов накопления погрешности D[∆t(t)].
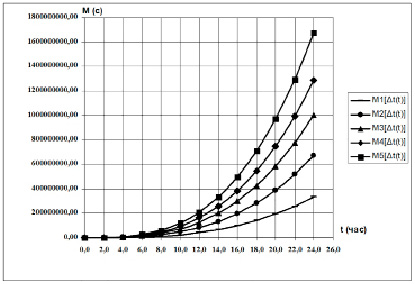
Рис. 3. Графики зависимости M[∆t(t)]
Коэффициенты а0, а1, а2…аn и с0, с1, с2…сn частных моделей процессов накопления погрешности отражают точностные показатели качества механических наручных часов и могут быть приняты в качестве их МХ. На основании вышеизложенного адаптивный алгоритм принятия решения о выборе соответствующего набора МХ наручных механических часов может быть представлен в виде следующих этапов:
1 этап. С помощью блока формирования временных интервалов, разработанного автором, структурная схема которого приведена в монографии автора [6, с. 72], и являющегося частью ИИС, реализуется процесс измерения погрешности интервалов времени в соответствии с формулой (1), далее определяются математические ожидания и дисперсии на всем интервале измерения, равном 24 ч, и определяется с помощью ИИС вид их изменения во времени (тренды). По полученному виду их изменений на интервале измерения осуществляется выбор частной модели процесса накопления погрешности в часах.
2 этап. Выбранная посредством ИИС конкретная частная модель процесса накопления погрешности подвергается проверке на адекватность: выбирается метод измерения информационного параметра, определяется объем выборки часов из партии часов для проведения статистических испытаний, формируются однородные выборки по полученным в ходе эксперимента значениям информационных параметров, обосновывается шаг дискретизации при выборе ряда значений информационных параметров на всем интервале измерений (например, 1 ч), выбирается критерий, подтверждающий стационарность n-х приращений, делается заключение по выбору процесса накопления погрешности на основе проведенных статистических испытаний.
3 этап. Если на втором этапе проверки модели на адекватность она признана адекватной и соответствует частным моделям, то вычисляются коэффициенты а0, а1, а2…аn и с0, с1, с2…сn, которые принимаются за точностные показатели (МХ) механических часов.
4 этап. Полученные значения МХ нормируются, т.е. определяются допустимые значения для принятых МХ.
5 этап. ИИС реализует два основных метода измрения (контроля) часов: выборочный и сплошной. При выборочном контроле определяется вид частной математической модели и соответствующие ей МХ часов. При сплошном контроле ИИС производит контроль всей партии часов по установленным на предварительном этапе наборам МХ.
Заключение
В настоящей работе рассмотрены вопросы, связанные с применением адаптивного алгоритма в ИИС для измерения и контроля наручных механическихчасов. Применение данного алгоритма в ИИС позволяет при решении ряда задач, связанных с измерением МХ механических наручных часов, повысить правильность принятия решения о количестве измеряемых характеристик точности часов на основании принятой модели процесса накопления погрешности. Предложенный автором адаптивный алгоритм идентифицирует процессы накопления погрешности механических часов и на их основе изменяет количество МХ, подлежащих измерению или контролю с заданной степенью достоверности.