Первоначально для описания процесса формирования шероховатости поверхности при токарной обработке использовался подход, при котором предполагалось, что обработанный профиль является регулярной кривой, образующейся вследствие совокупности кинематических движений при точении. Расчетная формула для определения величины среднеарифметического отклонения профиля была предложена В.Л. Чебышевым и имеет вид
Rz = S2 / (8 × r), (1)
где S – величина продольной подачи; r – радиус при вершине инструмента.
Позднее было установлено, что процесс более сложный и надо учитывать не только геометрию и кинематику процесса, но и характеристики срезаемого слоя, что было предложено А.И. Исаевым [1, с. 51]:
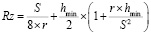, (2)
где hmin – минимальная величина толщины срезаемого слоя.
Дальнейшее развитие представлений о процессе формирования шероховатости поверхности было сформировано научной школой под руководством А.Г. Суслова [2]:
− вырывы обработанного металла с поверхности детали, вызванные адгезионным трением;
− наличие упругих и пластических деформаций;
− форма режущего инструмента;
− шероховатость режущей кромки инструмента;
− кинематика процесса резания;
− вибрации элементов технологической системы.
Зависимость, которая учитывает влияние данных факторов, была предложена в работах научной школы под руководством А.Г. Суслова и имеет вид [2]:
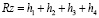, (3)
где h1 – высотная составляющая профиля обработанной поверхности, которая порождена кинематикой резания и геометрическими параметрами режущей части инструмента. Анализируя природу данных факторов, можно сказать, что составляющую h1 можно принять условно постоянной (детерминированной);
h2 – высотная составляющая профиля обработанной поверхности, которая порождена колебательными процессами изменения силы резания вследствие неравномерности срезаемого слоя, колебаний твердости обрабатываемой поверхности, и т.д. Анализируя природу данных факторов, можно сказать, что составляющую h2 принимаем переменной (стохастической);
h3 – высотная составляющая профиля обработанной поверхности, которая порождена пластическими и упругими деформациями элементов технологической обрабатывающей системы. Анализируя природу данных факторов, можно сказать, что составляющую h3 принимаем переменной (стохастической);
h4 – высотная составляющая профиля обработанной поверхности, которая образуется вследствие копирования исходных неровностей поверхности режущего инструмента.
Исходя из опыта исследований профилограмм шероховатости поверхности [3; 4, с. 20–25], можно сказать, что данный фактор также относится к постоянным (детерминированным).
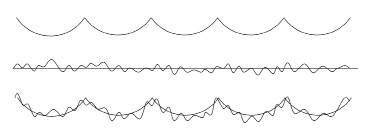
Тогда, с учетом того, что конечный микрорельеф обработанной поверхности (рис. 1, в) включает в себя как стохастические (рис. 1, б), так и детерминированные элементы (рис. 1, а), можно представить профиль в виде схемы.
Одни из первых исследований по изучению количественного состава микрорельефа поверхностей производились научной школой Ю.Р. Виттенберга [5], где рассматривалось применение теории вероятности и корреляционного анализа для установления уровня случайной составляющей γ, (вызванной прежде всего вибрациями режущего инструмента). Однако в данных работах преимущественно разрабатывался методологический аппарат для исследования, и они выполнялись без привязки к самому технологическому процессу. Поэтому в качестве развития данного направления необходимо изучить особенности микрорельефа в зависимости от требований к качеству поверхности.
Поэтому применение подхода по выделению систематических и случайных составляющих профиля шероховатости поверхности позволяет выявить факторы, которые оказывают наибольшее влияние. Это особенно важно при обработке закаленных сталей. Кроме того, из закаленных сталей чаще всего изготавливаются ответственные детали, к исполнительным поверхностям которых предъявляются повышенные требования, в том числе и по шероховатости поверхности. При этом использование шлифования для финишной обработки таких деталей также не всегда оправдано из-за процесса шаржирования обработанной поверхности, а также случайного характера микрорельефа поверхностей, обработанных шлифованием.
|
|
а) |
|
б) |
|
|
в) |
Рис. 1. Схема образования профиля шероховатости поверхности при токарной обработке
Цель исследования – изучение особенностей формирования шероховатости поверхности при токарной обработке закаленных сталей на основе количественного определения уровня систематической и случайной составляющих профиля.
Материалы и методы исследования
В качестве исходных данных использовались профилограммы поверхностей, обработанных чистовым точением. В качестве обрабатываемого материала – углеродистые конструкционные, легированные стали с твердостью более 35 HRC: сталь 45 и 45Х.
Экспериментальные исследования проводились на токарном обрабатывающем центре с наклонной станиной модели SuperJobber 500.
Режимы испытаний:
а) пределы скорости резания от 50 до 300 м/мин с постоянной подачей;
б) пределы подачи от 0,01 до 0,2 мм/об при постоянной скорости резания;
в) глубина резания от 0,1 до 0,3 мм при постоянных режимах обработки.
Исследование вибраций производили при помощи аппаратуры компании ZetLab: трехкомпонентный датчик вибраций АР20ХХ (диапазон частот 0–20000 Гц, погрешность, связанная с нелинейностью величин ±4, номер в ГРСИ 88508-23), анализатор спектра Zet 017 (погрешность по определению частоты ±1, номер в ГРСИ 39236-08), АЦП Zet 230 (динамический диапазон частот 100 Дб, частота преобразования 1–100 кГц, Номер в ГРСИ 55763-13, нелинейность преобразования ±1 Дб).
Измерение шероховатости производили при помощи профилографа-профилометра Абрис-ПМ7 (диапазон измерений по Ra 0,4–100 мкм, допустимая погрешность ±5, номер в ГРСИ 19876-00). Средства измерений прошли поверку на предприятии-изготовителе. В качестве режущего инструмента использовались стандартные токарные резцы с механическим креплением режущих пластин из наиболее распространенных в производстве твердых сплавов композит 01 (эльбор), композит 10 (гексанит), ВОК60.
Исследования обработанных профилей производились с использованием теории случайных процессов (на основе корреляционного анализа) [6, c. 51–63; 7], а также на основе фрактальной геометрии [8; 9]. При корреляционном анализе исследуемая профилограмма представляется в виде следующего преобразования:
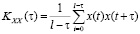, (4)
где τ – параметр по оси абсцисс (физический смысл временная задержка), принимает целые значения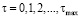 
; l – длина анализируемой профилограммы; x(t) – значение ординат анализируемого профиля.
Тогда, имея корреляционное преобразование профиля, можно определить искомый уровень случайной компоненты как соотношение дисперсии случайной составляющей Dγ и среднеквадратического отклонения профиля Rq:
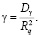(5)
В свою очередь, составляющие, входящие в выражение (5), можно определить следующим образом:
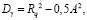(6)
где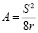 
– высота систематической компоненты профиля.
Среднеквадратическое отклонение профиля можно определить как значение автокорреляционной функции в нулевой точке:
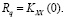(7)
Знание уровня случайной компоненты позволяет оценить долю систематической составляющей β:
β = 1 – γ. (8)
Шаг случайной составляющей Tγ профиля определяется как
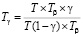, (9)
где T – шаг между неровностями реального профиля T = Sm; Tβ – шаг систематической составляющей Tβ = S; Sm – средний шаг неровностей:
Среднеарифметическое отклонение систематической (Raβ) и случайной составляющих (Raγ) определяется по формулам
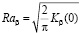, (10)
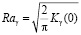. (11)
Использование фрактальной геометрии также дает возможность получить сведения о степени случайности в анализируемой кривой. Известно, что чем ближе значение фрактальной размерности D [8, 9] к 1,5, тем больше доля случайной составляющей. В данной работе фрактальная размерность профилограмм поверхностей деталей из закаленных сталей, обработанных точением, оценивалась при помощи показателя Херста (Н). Данный показатель определяется по следующей формуле [10, c. 91–96; 11; 12]:
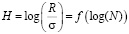, (12)
где R и σ – величина размаха и среднеквадратического отклонения профиля, вычисляемая при различных значениях переменной t, которая изменяется в пределах от 1 до N–1 (N – длина профилограммы).
Выражения для вычисления R и S имеют вид
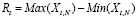, (13)
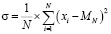. (14)
При этом показатель Херста и фрактальная размерность связаны между собой следующим соотношением
D = 2 – H. (15)
Учитывая изложенное выше, можно сказать, что чем ближе величина H к 0,5, тем уровень случайной компоненты в исследуемом профиле выше.
Авторами было разработано прикладное программное обеспечение, которое позволяет в том числе определять значения уровня случайной компоненты по формулам (4)–(11) и показателя Херста по формулам (9)–(15). Интерфейс представлен на рис. 2.
Результаты исследования и их обсуждение
Была получена зависимость уровня случайной компоненты от среднеарифметического отклонения профиля для поверхностей, обработанных чистовым точением заготовок из закаленных сталей (рис. 3).
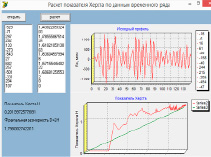
Рис. 2. Прикладное программное обеспечение
Аналитически данная зависимость задается выражением вида
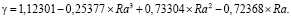(16)
Стандартное отклонение: σ = 0,03024. Коэффициент детерминации: R2 = 0,89945.
Значение коэффициента детерминации говорит о том, что зависимость (16) можно использовать для описания взаимосвязи между факторами.
На рис. 4 приведена зависимость показателя Херста от среднеарифметического отклонения профиля для поверхностей, обработанных чистовым точением заготовок из закаленных сталей.
Аналитически зависимость имеет следующий вид:
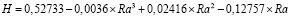. (17)
Стандартное отклонение: σ = 0,00843. Коэффициент детерминации: R2 = 0,97513.
Значение коэффициента детерминации говорит о том, что зависимость (17) адекватна.
На рис. 5 приведены зависимости мощности вибросигнала и шероховатости поверхности, полученные при точении закаленных сталей от ширины фаски износа резца.
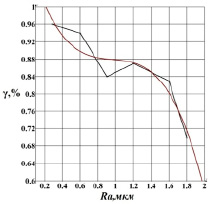
Рис. 3. Зависимость уровня случайной компоненты
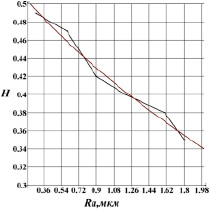
Рис. 4. Зависимость показателя Херста
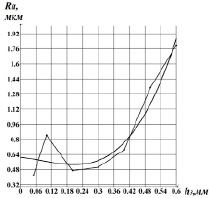
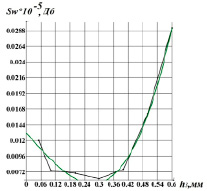
Рис. 5. Зависимости среднеарифметического отклонения профиля(Ra) и мощности вибросигнала (Sw) от ширины фаски износа (h3)
Было установлено, что коэффициент взаимной корреляции между Sw и Ra составляет 0,94. Также были получены зависимости указанных величин от подачи и скорости резания. Расчеты коэффициента взаимной корреляции показали, что он составляет от 0,86 до 0,95, таким образом, вывод о том, что в формировании шероховатости при обработке закаленных сталей чистовым точением преобладает влияние вибраций, подтверждается.
Заключение
Анализируя полученные результаты, можно сделать вывод о том, что в микрорельефе поверхностей деталей, которые изготовлены из закаленных сталей и обработаны чистовым точением, преобладает случайная составляющая. Важно отметить, что получилась высокая согласованность результатов, полученных с использованием разных методов исследования. Экспериментальные исследования вибраций и качества обработанной поверхности подтверждают обоснованность выводов теоретических расчетов.
Важным следствием для практики является то, что при уменьшении величины среднеарифметического отклонения профиля (Ra) наблюдается рост уровня случайной компоненты, причем для диапазона, который соответствует чистовой и финишной обработке (Ra < 1,6 мкм), уровень случайной компоненты превышает 75.
Таким образом, при решении задачи обеспечения заданных требований по шероховатости поверхности при токарной обработке необходимо, прежде всего, обеспечить такие условия, которые позволяют минимизировать влияние вибраций.