Большинство расчетов в области математического моделирования процессов обработки давлением реализуется с использованием зарубежных программных продуктов [1], здесь на первых местах находятся такие программные средства, как, например, DEFORM [2, 3] или ABAQUS [4]. Использование метода конечных элементов позволяет решить многие задачи, в том числе установить связи между термомеханическими параметрами и зеренной структурой металла [5]. Вместе с тем существуют и отечественные разработки, им недостаточно уделяется внимания, что совершенно не соответствует объявленным принципам импортозамещения. Система анализа процессов пластического деформирования РАПИД-2D разрабатывалась в Уральском федеральном университете для моделирования [6], в основном задач кузнечно-штамповочного производства (КШП). Первоначально метод решения затрагивал только постановки задач в 2D постановке (Copyright © Полищук Е.Г., Жиров Д.С., 2000–2004), но затем появились варианты вычислительного продукта для задач объемной деформации. Во всех случаях требовалось задание свойств вязкости среды, что обычно характерно для процессов горячей деформации и не характерно для процессов холодной деформации. Это объясняется тем, что в пакете программ реализован алгоритм решения, основанный на связи напряжений со скоростями деформации.
Прессование, как разновидность процесса обработки давлением, в какой-то мере ассоциируется с процессами КШП, но имеет свою специфику: целью ставится получить изделие большой длины, что достигается в традиционных приемах КШП кузнечной протяжкой. Некоторые задачи прессования в системе анализа процессов пластического деформирования РАПИД-2D были решены, например, для оценки роли теплопередачи при обработке латуней [7] и для оценки влияния компонентов тензора деформации на текстурообразование циркония [8]. Специфика процесса прессования по отношению к другим методам обработки давлением заключается в реализации больших и даже очень больших деформаций. Если речь идет о прессовании алюминиевых сплавов, то знание полей распределения деформаций позволяет оценить возможность прохождения процессов динамической рекристаллизации, что позволяет получить продукцию с заданным уровнем свойств [9] и заданной структурой [10]. Особенностью прессования алюминиевых сплавов является реализация процесса при малых скоростях нагружения. Это предопределяет торможение процессов рекристаллизации и получение изделия с более высоким уровнем прочности [11, 12]. Однако снижение скорости деформации в алгоритме решения задачи, основанном на зависимости напряженного состояния именно от скоростного фактора, делает неочевидным достижение конечного результата.
Целью работы является оценка возможности моделирования прессования в системе РАПИД -2D применительно к алюминиевым сплавам.
Схема деформации, постановка задачи моделирования и результаты решения
Рассматривается следующая схема деформации. Слиток 1 (рис. 1) размещен в контейнере 2 и выдавливается пресс-шайбой 3 через отверстие матрицы 4. В отличие от прессования тяжелых цветных металлов, где применяется прессовая прошивка, для прессования полых профилей из алюминиевых сплавов в слитке предварительно выполнено сквозное отверстие, через которое проходит игла 5. На выходе из матрицы формируется труба 6.
Геометрические параметры прессового инструмента:
− диаметр полости контейнера 650 мм;
− диаметр иглы 300 мм;
− диаметр отверстия матрицы 350 мм;
− угол наклона образующей матрицы к оси прессования 75°.
Процесс прессования осуществляется на горизонтальном гидравлическом прессе усилием 60 МН.
Кривая упрочнения алюминиевого сплава марки АМг6 задана на основании справочных данных, температура заготовки равна 490 °С, температуры контейнера и матрицы 400 °С и иглы 200 °С. Коэффициент теплопередачи принят равным 0,0559 Вт/(мм2*град). Показатели трения по Зибелю на стенке контейнера 0,8, на матрице и игле 0,2.
На рисунке области равного уровня соответствуют распределению степени деформации сдвига Λc, связанной со степенью деформации εc соотношением
Λc =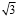 
* εc . (1)
Степень деформации при прессовании часто определяют приближенно по формуле
εc = ln [(Dз2 – dт2) / (Dт2 – dт2)] , (2)
где Dз, dт, Dт – диаметры заготовки, внутренний и наружный диаметры трубы соответственно.
Выполненный по формулам (1) и (2) расчет показывает, что Λc = 4,03, εc = 2,32.
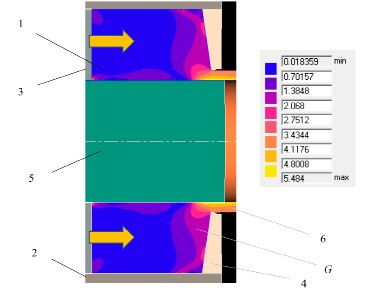
Рис. 1. Схема процесса прямого прессования слитка 1 из контейнера 2 пресс-шайбой 3 через матрицу 4 с помощью иглы 5 с получением трубы 6, показано распределение степени деформации сдвига Λ в очаге деформации G в виде цветных уровней с масштабной таблицей, стрелки – направление перемещения инструмента
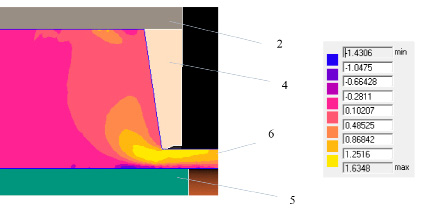
Рис. 2. Распределение компоненты тензора деформации εrz в очаге деформации в виде цветных уровней с масштабной таблицей, верхняя часть очага деформации, обозначения как на рис. 1
По рис. 1 видно, что максимальное значение Λ = 5,48 и оно превышает величину Λс 4,03, что объясняется тем, что Λс не учитывает сдвиговых деформаций, а их уровень при прессовании гораздо выше, чем при прокатке или волочении из-за резкого изменения траектории перемещения элементарной частицы.
Действительно, если рассмотреть отдельно распределение компоненты тензора деформации εrz (рис. 2), то ее максимальное значение равно 1,63. В соответствии с рис. 2 повышенный уровень компоненты εrz характерен для зоны, примыкающей к внутренней поверхности трубы. Но в соответствии с рис. 1 степень деформации выше в зоне, примыкающей к наружной поверхности. Для установления причин этого рассчитаем коэффициент вытяжки по толщине стенки λcr, что будет косвенно говорить о величине радиальной деформации
λcr = (Dз – dт) / (Dт – dт)] = 350/50 = 7, (3)
и коэффициент вытяжки в тангенциальном направлении
λcϕ = (Dз + dт) / (Dт + dт)] = 475/325 = 1,46.(4)
Проверка показывает, что произведение λcr * λcϕ отображает общий коэффициент вытяжки по площади, равный 10,23. Результаты оценки вклада радиальной и тангенциальной деформации в соответствии с формулами (3) и (4) приводят к выводу о том, что преобладают в процессе радиальные деформации, при этом они должны оказаться деформациями сжатия (укорочения). На рис. 3 приведено распределение компоненты тензора деформации εrr. Действительно, ближе к внутренней поверхности трубы радиальные деформации сжатия доходят до величины -2,04, что несколько больше радиальной логарифмической деформации εcr = lnλcr = 1,95. Как было показано выше, вклад тангенциальной деформации в накопленную степень деформации невелик и им можно пренебречь. Отсюда формулируется вывод, что накопленная степень деформации оказывается выше в зонах при внутренней поверхности трубы за счет радиальной компоненты тензора деформации.
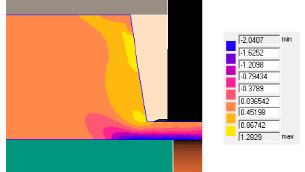
Рис. 3. Распределение компоненты тензора деформации εrr в очаге деформации в виде цветных уровней с масштабной таблицей, верхняя часть очага деформации
Рис. 4. Распределение компоненты тензора напряжений σzz в очаге деформации в виде цветных уровней с масштабной таблицей, верхняя часть очага деформации
Рис. 5. Распределение показателя напряженного состояния σ/T в очаге деформации в виде цветных уровней с масштабной таблицей, верхняя часть очага деформации
Существенным моментом в описании напряженного состояния является определение осевого напряжения σzz, поскольку его значение вблизи поверхности пресс-шайбы оказывается равным давлению прессования, а с его использованием удается рассчитать усилие прессования. Как видно из рис. 4, максимальное по модулю напряжение равно 511 МПа. Эта величина считается допустимой с позиции оценки прочности прессового инструмента.
Для оценки возможности разрушения металла используют показатель напряженного состояния σ/T, где σ − среднее нормальное (гидростатическое) напряжение, T – интенсивность касательных напряжений. Для оценки пластических свойств металлов применяют диаграммы разрушения, построенные в координатах степень деформации сдвига до разрушения – показатель напряженного состояния. В некоторых случаях в качестве второго аргумента применяют показатель Лоде.
Показатель напряженного состояния изменяется по ходу перемещения элементарной частицы в сторону выхода из очага деформации от -21 до 0. Это говорит о преобладании высоких напряжений сжатия, что вообще является характерным признаком процесса прессования и благодаря чему в этом процессе удается обрабатывать давлением малопластичные металлы и сплавы. При высоком уровне сжимающих напряжений вблизи поверхности пресс-шайбы сформирована жесткая зона, где металл не подвергается пластической деформации. Уровень гидростатических напряжений уменьшается вблизи поверхности матрицы, но именно здесь реализуются наибольшие деформации.
Вместе с тем в соответствии с теорией разрушения металлов показатель напряженного состояния рассматривают одновременно со значениями собственно накопленной деформации. Горячая обработка алюминиевых сплавов направлена часто на то, чтобы получить максимальную прочность готового изделия. Для этого надо затормозить процессы рекристаллизации, и это удается сделать в процессах горячей деформации именно для алюминиевых сплавов, обладающих очень высокой энергией дефектов упаковки. В области прессования это приводит к необходимости понижать скорость перемещения пуансона, что снижает скорость деформации и вообще-то снижает производительность оборудования. Эффект торможения рекристаллизации приводит к повышению прочности, но одновременно возникает опасность накопления такой деформации, при которой пластичность металла снижается до опасных уровней. Именно поэтому важно сопоставление диаграмм распределения среднего нормального давления или показателя напряженного состояния с распределением степени деформации сдвига.
Если вернуться к диаграмме (рис. 1), то можно отметить высокий уровень степени деформации сдвига в поверхностном слое трубы на уровне калибрующего пояска матрицы, здесь максимальное значение параметра равно 5,484. Показатель напряженного состояния в этом месте (рис. 5) близок к нулю, поскольку в зоне калибрующего пояска появляются поверхности, свободные от действия напряжений. В остальных зонах очага деформации напряжения окажутся сжимающими, что повышает пластичность металла. Таким образом, при прессовании трубы из алюминиевого сплава с заданными геометрическими параметрами опасной с позиции разрушения зоной является место выхода металла из отверстия матрицы.
Заключение
В работе показана возможность решения задачи прессования трубы из алюминиевого сплава с использованием отечественного программного продукта РАПИД-2D. В том числе построены поля распределения компонентов тензора деформации, степени деформации, показателя напряженного состояния. Сделан вывод о преобладающем влиянии радиальной компоненты тензора деформации на распределение степени деформации в продольном сечении готового изделия. Наиболее опасной с позиции трещинообразования является зона выхода металла из отверстия матрицы.