Поддерживаемое автором идеологически и личным участием (авторское) направление моделирования [1–3] тенсионных устройств (ТУ) от аналогичных других направлений [4, 5] отличается тем, что оно модели всех типов распространенных ныне ТУ довело до уровня расчетного алгоритма. Отсюда актуальность настоящей статьи.
Цель – продолжение развития авторского направления моделирования ТУ. Она предполагает частичное решение двух задач: 1) определение перспектив авторского направления, дополнение и изменение его теоретических положений; 2) проверка адекватности теоретических положений авторских методов моделирования практике использования ТУ.
Материалы и методы исследования
В статье используются материалы и методы хронологически первого [4] и второго [5] направлений моделирования ТУ, но в наибольшей степени – третьего (авторского) направления. Последние базируются на непосредственной практике стрельбы из современных ТУ, на ее наблюдении и оригинальном теоретическом обобщении. Такая практика тесно связана с правовой сферой [6]. Большинство авторов третьего направления [1, 2] – это преподаватели дисциплин из областей математики и информатики в технических вузах. Они используют в преподавании [7] эти модели, поскольку студенты способны их понять. Полная проверка адекватности теоретических положений третьего направления требует постановки целенаправленных опытов с использованием недешевых измерительных приборов, которыми автор не располагает. Для частичной проверки адекватности этих положений в настоящей статье на их основе ставятся умозрительные опыты и обосновываются некоторые факты, известные из практики применения ТУ.
Результаты исследования и их обсуждение
Настоящая статья в силу ограниченности объема обсуждает лишь современные распространенные ТУ. Ниже будут часто использоваться ссылки на рисунки, формулы, фрагменты текста из [1], где опубликована последняя полная версия теоретических положений авторской модели ТУ.
1. Стратифицированная структура авторской модели. Модели третьего направления целесообразно стратифицировать. На верхнем уровне будет располагаться самая общая модель – метамодель ТУ, самые общие понятия для обсуждения ТУ, включая типологию ТУ. На нижнем уровне на основе положений метамодели будут моделироваться особенности конкретных типов ТУ и более конкретных положений. В дальнейшем развитии третьего направления, вероятно, таких уровней станет больше. Отрасль ТУ (и в теоретическом, и в практическом аспекте) тем самым становится ближе к технологиям открытых систем, которые зародились в 1960-е гг. в области информатики, а ныне повсеместно работают в технической сфере. Данный подраздел 1 вводит понятие метамодели ТУ. Ниже подразделы 2, 3, 4, 5, 7, 8, 9 и 10 (в части новой методики сравнения различных ТУ по интегральному коэффициенту) совершенствуют эту метамодель по сравнению с материалами из [1].
2. Базовые состояния ТУ. Для любого ТУ, имеющего плечи и тетиву, предлагается выделять три базовых состояния: походное состояние (тетива снята с плеч, чтобы они не подверглись пластической деформации); боевое состояние (тетива надета на плечи, но не натянута); состояние готовности к выстрелу (тетива полностью натянута в соответствии с задачами предстоящего выстрела, стрела находится на специальной полочке, ниже приведено ее определение). Холостые выстрелы (без стрелы) могут привести к поломке ТУ и травмированию стрелка. Можно говорить и о переходных состояниях ТУ в процессе перехода от одного базового состояния к другому.
3. Базовые авторские формула и теорема. В [1] нет ни самой общей авторской (базовой) формулы, ни формулировки авторской базовой теоремы, лежащих в основе третьего направления моделирования.
P = Tarr + Tdev + Pfri. (1)
Базовая формула – это (1), где P – потенциальная энергия, запасенная стрелком при натягивании тетивы; Tarr – кинетическая энергия стрелы (arrow – так в статье указывается перевод термина на английский) при отрыве от тетивы; Tdev – суммарная кинетическая энергия всех движущихся частей метательного устройства (device); Pfri – потери потенциальной энергии на преодоление трения (friction) стрелы о ТУ при разгоне; (1) – следствие (7) из [1, с. 269]. Используя (1), легко вычислить Tarr, Pfri из общего курса физики-механики, P легко вычисляется благодаря идее А. Шалыгина [3] о кривой упругости ТУ. Идея Р. Фокина [1, с. 267–269] позволяет легко вычислить Tdev при помощи введенных им понятий mred – приведенной массы ТУ, kred – приведенного коэффициента для каждой точки ТУ с тетивой в боевом положении, а также (3), (4) из [1, c. 268]. Назовем условием приведения для ТУ в боевом состоянии наличие kred, независимого от varr для каждой точки ТУ, имеющей скорость v, если выполняется равенство v = kred varr. Базовая теорема: если ТУ удовлетворяет условию приведения, тогда такое ТУ адекватно представляется в виде механической модели ТУ. Смысл механической модели ТУ (лежащей в основе всех авторских вычислений), смысл всех величин, упомянутых в этом абзаце, а также доказательство базовой теоремы приведены в [1, c. 267–269]. Вывод: если ТУ удовлетворяет условию приведения, то к нему применима авторская механическая модель ТУ и все вычисления из [1].
4. Коэффициент полезного действия (КПД, keff) физической системы ТУ – стрела. В [1, с. 269] его определение сформулировано так: keff = Tarr/P.
marr/(marr + mred) = Tarr/(Tdev + Tarr) =
= Tarr/(P – Pfri), (2)
keff ≈ marr/(marr + mred) при малом Pfri. (3)
(2), (3) – следствие (13)–(15) из [1, с. 269]. У всех ТУ Pfri < 0,05 Tarr и mred >> marr, так что (3) актуальна, поэтому keff << 0,5 и keff ~ marr.
5. Составные части и обвес ТУ. Составные части ТУ – это части, из которых состоит ТУ непосредственно. Обвес ТУ – это дополнительные аксессуары для эксплуатации ТУ. В версии авторской модели ТУ, соответствующей данной статье, могут использоваться: составные части ТУ (рис. 1 и 2): райзер (riser); корпус арбалета, плечи; тетива и тросы; супрессоры (о них рассказано ниже в подразделе 7); обвес ТУ: полочка (arrow rest); стабилизаторы (stabilizers); прицел (sight) и пип-сайт (pip-site); релиз (release).
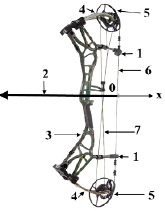
Рис. 1. Блочный лук в боевом состоянии: 1 – супрессоры верхний и нижний; 2 – закрепленная на тетиве стрела; x – ось натяжения тетивы с 0-точкой этой оси;3 – райзер; 4 – плечи верхние и нижние; 5 – блоки верхний и нижний; 6 – тетива; 7 – тросы

Рис. 2. Лук выживания в походном состоянии (справа сверху) и в боевом (на переднем плане): 1 – райзер; 2 – парные плечи; 3 – тетива
Плечи – это упругие сгибаемые части ТУ. Плечи бывают как единые (one piece), так и симметричные парные – верхние и нижние у луков; правые и левые у арбалетов. Современные блочные луки и арбалеты как плечи часто используют четыре симметричные упругие планки плеч – правая верхняя, правая нижняя, левая верхняя, левая нижняя. Если плечи ТУ полностью сделаны из фибергласса, то для такого ТУ можно тетиву с плеч никогда не снимать. Фибергласс – материал без памяти (без пластической деформации) при изгибе.
Райзер, корпус арбалета функционально аналогичны. Это средняя несгибаемая часть ТУ, к которой крепятся плечи. Корпус арбалета часто имеет приклад, а также направляющую для стрелы, замок для фиксации тетивы в состоянии готовности к выстрелу и спусковой механизм со спусковым крючком.
Тетива, тросы, релиз. На блочном ТУ тетива при натяжении сматывается с больших радиусов блоков, заставляя их вращаться, при этом тросы наматываются на малые радиусы блоков, укорачиваясь и заставляя плечи сгибаться. Релиз зацепляется за тетиву блочного лука и закрывает замок, затем стрелок за рукоятку релиза растягивает тетиву до состояния готовности к выстрелу и нажимает спусковой крючок на релизе, открывая при этом замок и спуская тетиву. Неблочные луки не используют ни тросов, ни релиза.
Полочка. На ней лежит стрела во время разгона. Эффективность полочки тем выше, чем меньше трение стрелы о нее при разгоне. У традиционных луков полочкой является перчатка на руке стрелка, держащей лук. Иное запрещено правилами соответствующих соревнований. У правши левая рука держит лук, а правая – натягивает и спускает тетиву. Для классических луков аналогичные правила разрешают использовать только одноразовые и магнитные полочки, они эффективнее лишь чуть-чуть. Аналогичные правила для блочных луков разрешают лишь волосяную и падающую полочки. Волосяная полочка эффективнее и магнитной, и одноразовой. Падающая полочка сводит трение стрелы к нулю.
Стабилизаторы гасят вибрации ТУ с целью увеличения кучности попадания стрелы. Их используют на арбалетах, классических и блочных луках. На традиционных луках любой обвес запрещен, и применяется интуитивная стрельба без явного прицеливания.
Прицел и пип-сайт. На блочных и классических луках прицелы крепятся к райзеру чуть выше полочки, они могут быть оснащены линзами. Пип-сайт вплетается в тетиву напротив глаза стрелка и дает ему возможность смотреть сквозь тетиву лука и прицел одновременно, обеспечивая визирование через две точки. Без пип-сайта визирование возможно лишь через одну точку в прицеле, при этом вторая точка находится в хрусталике глаза стрелка, смещаясь вместе с движениями его головы. Оптические прицелы (с линзами) используют для стрельбы далее 30 м.
6. Тяжелая и легкая стрелы в авторской модели. При выстреле энергия (P – Pfri) целиком преобразуется в кинетическую (Tdev + Tarr), но в какой пропорции между ними?
Tdev = mred varr2 / 2, (4)
Tarr = marr varr2 / 2, (5)
Tarr / Tdev = marr / mred, (6)
Tarr = K (P – Pfri), (7)
где K = marr / (marr + mred),
P ≈ P – Pfri при малом Pfri, (8)
Tarr ≈ K P при малом Pfri и
K = marr / (marr + mred). (9)
Из механической модели ТУ следует, что и поршень, и стрела движутся со скоростью стрелы varr в момент отрыва стрелы от тетивы, отсюда (4), (5). Из них следует (6), а из него – (7). В конце подраздела 4 указано, что для любого ныне распространенного ТУ Pfri мало, отсюда (8). Из (7), (8) следует (9). Пусть два выстрела сделаны из того же ТУ стрелами с массами marr2 > marr1, очевидно, тогда varr1 > varr2. Можно доказать, что K из (9) возрастает при росте marr и фиксированной mred, отсюда Tarr2 > Tarr1. Практика этот факт подтверждает. Аналогично из (3) следует, что keff2 > keff1.
7. Роль супрессоров в авторской модели. На рис. 1: ось x направлена противоположно стреле, 0-точка оси x – это точка пересечения оси x и тетивы в боевом положении: при этом тетива лежит на резиновых подушечках верхнего и нижнего супрессоров, стрела лежит на падающей полочке, нок стрелы (ее задний конец) прикреплен к тетиве. Затем тетива натягивается по оси x. На рис. 1, а, из [1, с. 268] показан блочный лук с тетивой, натянутой до координаты S оси x с силой натяжения F. Там был показан блочный лук только с нижним супрессором. При x = Smax наступает состояние готовности лука к выстрелу. Затем, согласно [1, с. 267], стрелок спускает тетиву в момент времени t = 0, а при t = t* лук снова достигает боевого положения, а тетива – ненатянутого состояния при x = 0. В момент t = t* из-за супрессоров тетива далее не может двигаться левее в зону x < 0, поэтому стрела от тетивы отрывается и продолжает далее самостоятельный полет. Скорость стрелы varr(t) зависит от времени t, varr(0) = 0, varr(t*) максимальна, далее при t > t* уменьшается varr(t). По соображениям, подробно изложенным в [1, с. 267], система ТУ – стрела нами рассматривается только при t = t*, поэтому мы и ввели обозначение varr = varr(t*). Модель третьего направления, рассматриваемая в [1], неявно предполагала наличие супрессоров на ТУ. При этом отрыв стрелы происходит при x = 0. Но не у всех ТУ имеются супрессоры. В этом случае после спуска тетивы при некоторых t > t* она зайдет в область x < 0, в этой области натяжение тетивы будет активно гасить скорость стрелы, ее отрыв от тетивы произойдет при t = t**, t** > t*, varr(t**) < varr(t*). После отрыва стрелы от тетивы при t = t** будут иметь место большие колебания плеч и тетивы ТУ, постепенно разрушающие ТУ. Наличие супрессоров – это положительный фактор, способствующий уменьшению паразитных колебаний, росту скорости стрелы и сохранности ТУ.
8. Расширение множества ТУ, совместимых с авторским моделированием. В [6] содержатся определения лука и арбалета. Оба они – метательные устройства, оснащенные тетивой и упруго сгибающимися плечами, метательный снаряд у обоих – стрела. Но полностью натянутая тетива фиксируется у лука мускульной силой стрелка, а у арбалета – специальным механическим устройством, замком тетивы. В [1] методами третьего направления моделировались блочные, традиционные английские, турецкие, монгольские, луки, моделировались и арбалеты с аналогичными плечами, а значит – все распространенные арбалеты. Выше, в подразделе 3, было показано: если не рассмотренное ранее ТУ [1] удовлетворяет условию приведения, то оно может пополнить этот список.
В [1] не упоминались луки выживания, классические (олимпийские) луки. Классические луки легко собираются и разбираются на три основные части: райзер и парные симметричные плечи (нижнее и верхнее). Если такое плечо точек перегиба не имеет, то лук с точки зрения авторской модели не отличим от Long bow. Если имеет одну точку перегиба, то от турецкого лука. Если две точки перегиба, то от монгольского лука. Лук выживания (рис. 2) – складной, он аналогичен Long bow. Все они совместимы с авторским моделированием.
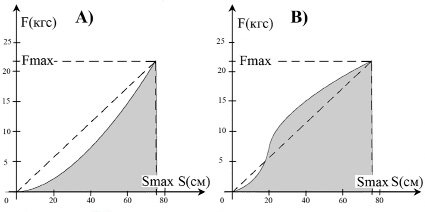
Рис. 3. Кривая упругости F(S), где F измеряется в килограммах силы (кгс), а S – в см: A) для ТУ с R = 1 (Long bow Top Archery, Fmax ≈ 21,5 кгс при Smax ≈ 76 см); B) для рекурсивных ТУ (традиционный монгольский лук Top Archery, Fmax ≈ 21,5 кгс при Smax ≈ 76 см)
Давно известны праща и метательные ножи, но мало кто владеет искусством их применения. Недавно появились пневматические луки и арбалеты, распространенными они тоже не являются. Автору непонятно, чем они отличаются друг от друга. Это пневматическое гладкоствольное дульно-зарядное ружье, где вместо пули используется специальная стрела, по длине сравнимая со стволом. Все упомянутые в данном абзаце метательные устройства не являются ТУ и не совместимы с авторским моделированием.
9. Обсуждение понятия степени рекурсивности ТУ и их типажа. В [1, с. 271] было описано авторское понятие степени рекурсивности лука (r). Для вычисления r предлагалось просто считать количество дуг, из которых состоят плечи данного лука. Например, у традиционного турецкого лука получается r = 3 согласно рис. 3, B, из [1, c. 270]. В силу симметричности этого лука правая и левая дуги работают синхронно как одна дуга, а средняя дуга может работать несинхронно с ними. Поэтому введем еще одну величину R – степень асинхронной рекурсивности, в данном случае R = 2. При натяжении тетивы m из R групп синхронных дуг плеч сгибается и n групп – разгибается, так вычисляется пара рекурсивности (m, n), в данном случае получается (1; 1).
Точное правило измерения r состоит из пяти пунктов:
1) Дугой называем гладкую кривую без точки перегиба.
2) Считаем количество дуг в составе плеч ТУ.
3) Несколько дуг считаем за одну дугу, если эти дуги могут быть совмещены параллельным переносом.
4) Считаем количество дуг по приведенным выше правилам 1–3 не только в боевом положении ТУ, но также и в ближайших к нему промежуточных положениях по мере малого натяжения тетивы.
5) Берем min по малым S в наших измерениях r по пункту 4.
Пункт 6 измеряет R:
6) Если в силу симметричности конструкции ТУ несколько дуг его плеч работают синхронно, то считаем их за одну.
Вычислим r, R и (m; n) для различных типов неблочных луков: A) Long bow: 1, 1 и (1; 0). B) Турецкий лук: 3, 2 и (1, 1). C) Монгольский лук: 5, 3 и (1; 2). D) Лук с райзером и парными плечами (плечо без точек перегиба): 2, 1 и (1; 0). E) Лук с райзером и парными плечами (плечо с одной точкой перегиба): 4, 2 и (1, 1). F) Лук с райзером и парными плечами (плечо с двумя точками перегиба): 6, 3 и (1, 2). Для неблочных арбалетов с соответствующими плечами результаты будут те же самые.
Исходя из предыдущего абзаца видно, что теперь r ∈ {1, 2, 3, 4, 5, 6}, появились четные r, но только при r ≥ 3 ТУ может оправданно считаться рекурсивным. А среди неблочных ТУ реально типов 3, а не 6. Показатель R более удачный: R ∈ {1, 2, 3}, эти значения соответствуют реальным типам неблочных ТУ, при R = 1 ТУ не может оправданно считаться рекурсивным. При R = 2 и 3 (рекурсивные ТУ) различия небольшие, турецкий лук был изобретен на несколько веков позднее монгольского, он проще в изготовлении и ремонте, дешевле последнего и почти что не хуже. Различия этих типов ТУ ярко проявляются по виду F(S) – кривой упругости [3], рис. 3 содержит уточненные данные автора. На рис. 3, A, виден очень сильный рост F, если неосторожно увеличить S, то упругий изгиб плеч перестанет быть таковым и плечи сломаются. На рис. 3, B, видна «ступенька» – два биения кривой F(S) около диагонали прямоугольника, для рекурсивных ТУ таких биений может быть и больше. При R = 3 самая плохая кучность попадания стрел, при R = 1 она значительно лучше. Для блочных ТУ график на рис. 2, A, из [1, с. 270] адекватен.
10. Авторское сравнение ТУ по kint – интегральному коэффициенту. Естественно сравнение ТУ по varr – разгонной скорости стрелы, но это не всегда адекватно. Распространено, например, мнение, что блочный лук – самый скоростной, рекурсивный (монгольский, например) – хуже, а Long bow – самый плохой из них. Практика показывает нечто похожее. К этому естественно добавить: «при прочих равных условиях». Каковы они? Естественное, например, условие – это одинаковые marr; Fmax; Smax для этих трех луков. Можно использовать одинаковую стрелу для этих трех луков. Труднее найти три лука различных типов, у которых Fmax и Smax соответственно были бы одинаковыми. Мы предлагаем эти три лука сравнивать по kint, чем он больше, тем лучше. Мысленным экспериментом мы обоснуем, что это почти то же самое, что сравнивать их по varr. В [1, c. 270] вводятся авторские понятия kint (способность ТУ запасать потенциальную энергию P при натяжении тетивы) и идеального ТУ (в этом смысле). Это идеальное ТУ имеет kint = 1, причем 0 ≤ kint ≤ 1 для любого ТУ.
Pидеал = Fmax Smax, (10)
P = kint Pидеал. (11)
(10), (11) – следствие (16)–(18) из [1, c. 270]. Запасенная ТУ потенциальная энергия равна площади подграфика F(S) для S ∈ [0; Smax]. Для идеального ТУ – это площадь прямоугольника, равная Fmax Smax, а (11) представляет смысл kint. Согласно рис. 2, A, из [1, с. 270] для блочного лука площадь подграфика F(S) лишь немногим меньше площади этого прямоугольника, а kint ∈ [0,7; 0,9]. Согласно рис. 3, A, для Long bow (R = 1) площадь подграфика F(S) немного меньше площади треугольника, указанного пунктирными линиями, а kint < 0,5. Согласно рис. 3, B, для рекурсивного лука (R = 2, 3) площадь подграфика F(S) немного больше площади этого треугольника, а kint > 0,5. На рис. 3, A и B, эти подграфики отмечены серым фоном, а графики относятся соответственно к традиционным английскому и монгольскому лукам, имеющим одного производителя «Top Archery» и очень близкие характеристики. Луки тех же типов, но с другими характеристиками будут иметь для F(S) похожие кривые соответственно. Из (5) следует, что кинетическая энергия стрелы Tarr ~ varr2. Пусть у наших трех луков (блочного, монгольского, английского) одинаковы keff (КПД), Smax, Fmax и marr, а также пусть kint_анг = 0,4, kint_мон = 0,6, kint_блоч = 0,8 – это соответствует указанным выше условиям. Тогда частное скоростей разгона стрелы будет равно квадратному корню частного соответствующих интегральных коэффициентов:
varr_мон / varr_анг = sqrt (kint_мон / kint_анг) =
= sqrt (0,6/0,4) = sqrt (1,5) ≈ 1,225;
varr_блоч / varr_мон = sqrt (kint_блоч / kint_мон) =
= sqrt (0,8/0,6) ≈ sqrt (1,333) ≈ 1,155.
Это мысленный эксперимент, но практика подтверждает его результаты.
11. Известные техники стрельбы из луков различных типов находят объяснение в результатах авторского моделирования. Для блочного лука F(Smax) << Fmax – рис. 2, A, из [1, с. 270], следовательно, в состоянии готовности к выстрелу стрелок может долго прицеливаться – он не устанет долго держать максимально растянутую тетиву. Для всех остальных луков F(Smax) = Fmax (рис. 3, A, B), следовательно, стрелок сильно устанет от долгого удержания максимально растянутой тетивы и не сможет стрелять точно. Для этих луков оптимальна иная техника стрельбы: нужно успеть прицелиться в процессе натяжения тетивы и затем – немедленно ее спустить и произвести выстрел.
Заключение
Были решены все поставленные в статье задачи: задача 1 (определение перспектив авторского направления, дополнение и изменение его теоретических положений) – ее решение дано в подразделах 1, 2, 3, 4, 5, 7, 8, 9 и 10 (в части новой методики сравнения различных ТУ по интегральному коэффициенту); задача 2 (проверка адекватности теоретических положений, авторских методов моделирования практике использования ТУ) – ее решение дано в подразделах 6, 10 (в части обоснования известных результатов сравнения скоростных характеристик блочного, традиционных монгольского и английского луков) и 11. Таким образом, было продолжено развитие авторского направления моделирования ТУ, а следовательно, была достигнута поставленная в статье цель исследования.



