Распределение годовой учебной нагрузки преподавателей, или научно-педагогических работников (НПР), кафедры является достаточно сложной проблемой с математической точки зрения [1, 2]. Обычно в научных работах, посвященных этой задаче, рассматривается распределение нагрузки между НПР, но не рассматривается вопрос автоматизации учета формальных требований, связанных с оплатой труда НПР. Данный вопрос состоит в следующем. Когда станет известно, что конкретно будет преподавать данный НПР, нужно распределить его нагрузку между индивидуальными планами (ИП), к которым, например, во ФГБОУ ВО «ЧГУ им. И.Н. Ульянова» относятся следующие виды:
− штатная (основная) нагрузка Ss (число часов зависит от доли ставки и должности);
− нагрузка при работе по совместительству Sv. Также зависит от доли ставки и должности и не может быть более половины ставки;
− почасовая нагрузка Sc. Общее ограничение для такого ИП – 300 часов с учетом суммирования с почасовой оплатой на других кафедрах (при наличии);
− учебные поручения Su. Подобно почасовой нагрузке, но с ограничением 200 часов;
− работа на условиях договора гражданско-правового характера (ГПХ). Обычно такие работники одновременно не имеют других ИП, поэтому в данном случае перераспределять часы между ИП не требуется. Поэтому далее в формулах такая работа не учитывается.
В небольшом числе научных работ имеются некоторые связанные с соблюдения норм нагрузки результаты. Например, в [3] рассмотрена программа «1С:Университет ПРОФ», где можно распределять учебную нагрузку. Одной из возможностей является установка и проверка норм нагрузки сотрудников.
В [4] в том числе затронуты вопросы учета единиц нагрузки при распределении нагрузки, но не сообщается о разработке программного средства. В [5] предложен подход, при котором распределение производится с учетом Ss ≤ 900 в связи с приказом Минобрнауки России от 22 декабря 2014 г. № 1601. В [6] сообщается о компьютерной программе информационной системы «РасчетРаспределение», где, помимо прочих функций, имеется автоматизированное разделение часов преподавателя на Ss и Sc. Однако о подробностях не сообщается, а разновидностей ИП не пять вышеперечисленных, а всего две.
Таким образом, имеется множество программ, результатом которых является то, что общая нагрузка и соответствующая сумма часов для преподавателя становятся известны, поскольку каким-то образом нагрузку между преподавателями распределили. После этого требуется распределить эти часы по разным ИП, учитывая, что нельзя превышать нормативы по ИП, а также нежелательны значения ниже нормативов. Здесь можно выделить строгие ограничения и критерии оптимальности, сводящиеся к целевой функции. В связи с этим возникает необходимость решить некоторую оптимизационную задачу. Для решения таких задач могут применяться различные метаэвристические алгоритмы.
Целью работы является применение генетического алгоритма (ГА) для оптимизации распределения часов учебной нагрузки для каждого преподавателя между ИП его нагрузки.
Решаемые задачи: формулирование целевой функции, разработка алгоритма решения задачи, программная реализация, проведение вычислительного эксперимента.
Материалы и методы исследования
Исследование проводится с использованием данных о нагрузке НПР кафедры компьютерных технологий за 10 лет. Для исследования используются следующие методы: вычислительный эксперимент, метод анализа, метод измерения, усреднение значений, машинное обучение.
Формулирование целевой функции
Вначале для каждого НПР нужно задать величины Es, Ev, Ec, Eu – минимальное число часов соответственно для штатной нагрузки, нагрузки по совместительству, почасовой нагрузки и учебных поручений, а также Xs, Xv, Xc, Xu – максимальное число часов соответственно для почасовой нагрузки, штатной нагрузки, учебных поручений и нагрузки по совместительству. Для этого учитываются нормы значений по должностям и доля ставки, а также вручную могут устанавливаться значения для почасовой нагрузки и для учебных поручений с учетом работы на других кафедрах. Примеры некоторых норм, установленных кафедрой компьютерных технологий: для профессора Es = 800 ч, Xs = 820 ч, для старшего преподавателя Es = 880 ч, Xs = 900 ч. Если ставка неполная, эти размеры умножаются на долю ставки, например на 0,25.
Эти нормы основаны на Положении о формировании штатного расписания ФГБОУ ВО «Чувашский государственный университет имени И.Н. Ульянова», где установлена следующая дифференциация: для профессора Es = 750 ч, Xs = 850 ч, для старшего преподавателя Es = 825 ч, Xs = 900 ч, и др. Кафедральные нормы жестче университетских потому, что в среднем по НПР должно быть Ss ≥ 860, иначе, согласно указанному Положению, почасовой оплаты производиться не будет. Подобные ограничения существуют и в других вузах, например информация об этом сообщается в [5].
Правила заполнения ИП для некоторого НПР следующие.
1. Если часов больше, чем по норме для Ss, то избыток переводится в Sv или в Sc.
2. Sv должно быть в допустимом диапазоне с учетом доли ставки. Если для этого часов недостаточно, часы направляются только в Sc, а если много, то в Sc направляется избыток.
3. Согласно вышеназванному Положению, должно выполняться неравенство Sc ≤ 300. Поэтому избыток Sc переходит в Su. Но если имеются Su, то должно быть Sc ≥ 299.
4. Должно быть Su ≤ 200. Избыток надо распределить между другими НПР.
Для формализации этих и других правил предлагаются следующие 15 правил для вычисления значения целевой функции F (исходно F = 0):
1. Если Ss < Es, то F соответственно увеличивается: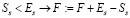 
.
2. Увеличение F, если Ss > Xs: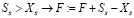 
.
3. Аналогичным образом для величин Sv , Xv и Ev:
; 
.
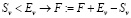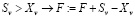4. Если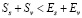 
, то F увеличивается на соответствующую разность. Дело в том, что, если Ss немного меньше Es, а Sv > Ev, это может взаимно компенсироваться. Но если отклонения настолько большие, что не компенсируются, то их нужно учитывать:
.
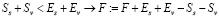5. По аналогии, если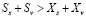 
, F также соответственно увеличивается:
.
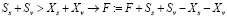6. Для величины Su учитывается превышение ею верхнего предела – Xu:
.
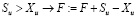7. Для Sc требования более строгие, поэтому правило сходно с предыдущим с учетом Xc и Ec, но с умножением на штрафной коэффициент, например на 10:
; 
.
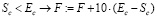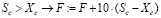При очень высоком значении штрафного коэффициента ожидается, что задача безусловной минимизации становится «тяжелой», т.е. время вычислений становится неприемлемо большим [7, с. 291]. Поэтому выбрано не слишком большое произвольное число (10) и многократно проведен процесс оптимизации нагрузок, показавший, что число 10 является приемлемым.
8. Согласно вышеуказанному Положению, нагрузка в одном семестре должна быть не более 2/3 общегодовой нагрузки, а кафедральные требования строже. Таким образом, количество часов основной нагрузки во втором полугодии Ss2 не должно быть меньше количества часов основной нагрузки в первом полугодии Ss1, например в 0,45 раза, а больше – в 2,1 раза. Иначе избыточные или недостающие часы делятся на некоторый коэффициент, например на 100, и суммируются с F:
.
.
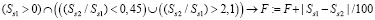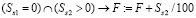9. Аналогичное правило для нагрузки по совместительству:
.
,
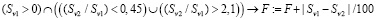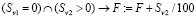где Sv1, Sv2 – количество часов по совместительству соответственно в первом и втором полугодиях.
10. Такое же правило действует для почасовой нагрузки, но коэффициенты другие: 0,2 и 5 вместо 0,45 и 2,1. Это связано с тем, что можно оформлять заявления на оплату не более 4 часов в день, а с этим возможны проблемы, если все 300 часов будут в одном полугодии:
.
,
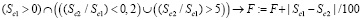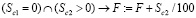где Sc1, Sc2 – почасовая нагрузка соответственно в первом и втором полугодиях.
11. Подобное предыдущему правило действует для учебных поручений, и здесь другие коэффициенты: 0,4 и 2,5 вместо 0,45 и 2,1. Это нужно на случай увольнения преподавателей в середине года: НПР мог получать оплату за непроведенные занятия, так как они во втором полугодии, а учебные поручения оплачиваются равномерно в течение года. Либо он мог все провести в первом полугодии, а оплату получить только за половину:
.
,
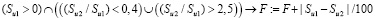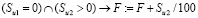где Su1, Su2 – количество часов учебных поручений соответственно в первом и втором полугодиях.
12. Возможно, что данному НПР нежелательно наличие почасовой оплаты на первое полугодие по личным причинам, а ему такую нагрузку навязывают. Тогда к F добавляется количество таких часов: возможно,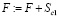 
.
13. Аналогичное правило действует для второго полугодия: возможно,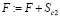 
.
14. Если Ss > 900 либо нагрузка по доле ставки Rs больше соответствующего количества часов, то это нарушение вышеупомянутого приказа, и к F добавляется превышение, умноженное на некий штрафной коэффициент, например 10:
.
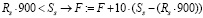15. Аналогично для доли нагрузки по совместительству Rv:
.
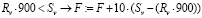Применение перечисленных выше правил приводит к увеличению значения F в том случае, когда та или иная нагрузка выходит за границы интервалов. При этом для правил 12 и 13 следует границей интервала считать 0.
Разработка алгоритма оптимизации целевой функции
Распределение часов между ИП является задачей дискретной оптимизации:
F = F(O1, …, OC) → min,
где F – целевая функция;
C – число элементов нагрузки. Элемент нагрузки (рисунок) – это совокупность данных о части нагрузки некоторого НПР (идентификатор, название дисциплины, сведения об учебной группе и объединении в поток, количество часов общее и по видам работ – лекции, курсовые и иное, вид ИП, полугодие), которая целиком может принадлежать только одному ИП;
Oi – номер разновидности ИП для i-го элемента нагрузки, принимающий значения от 0 до 3, где i = 1,…,C. Значению 0 соответствует ИП основной нагрузки, 1 – почасовой, 2 – по совместительству, 3 – учебных поручений.
Для решения этой задачи в данной работе применяется генетический алгоритм Genitor [8]. Алгоритм использует вариант распределения нагрузки, полученный в результате применения следующей процедуры с именем N7Click. Вначале значения Ok номера ИП устанавливаются в –1 для всех элементов нагрузки Nk, где k = 1,…,C.
Затем поочередно для каждого Nk, где k = 1,…,C, выполняются шаги.
1. Переменной Min присваивается 10000.
2. Поочередно для каждого Oi, где i = 1,…,C, если Oi = –1, выполнить:
2.1. Вычисляется F0 – это значение F при Oi = –1.
2.2. Значение Oi устанавливается последовательно от 0 до 3 – это номер вида ИП. При каждом таком значении, обозначаемом j:
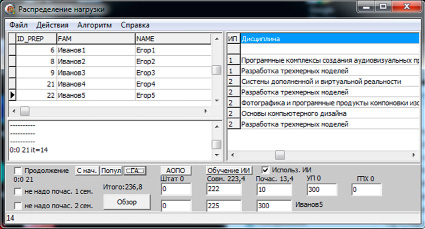
Вид главного окна разработанной программы. Слева вверху – список преподавателей, слева в центре – вывод результатов оптимизации, справа – список элементов нагрузки, снизу – элементы управления и некоторые установки
2.2.1. Вычислить значение F.
2.2.2. Если F – F0 < Min, то присвоить Min = F – F0 и запомнить значения i, j в переменных i1, j1.
3. Присвоить значение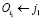 
.
В итоге все Nk получают действительные значения Ok, формируя первую из особей ГА, каждая из которых представляет собой набор генов, т.е. значений Oi, где i = 1,…,C.
Исходная популяция состоит из заданного числа P ∈ [30,60] особей: {Z}, i = 1,…,P, и формируется следующим образом. P раз выполняются такие же действия, как при вызове процедуры N7Click, связанные с очередной особью, однако имеется особенность. Она применяется для номеров особей i > 1 и состоит в том, что при вычислении очередного F до и после изменения вида ИП к результатам добавляются случайные числа, меньшие 20.
В ГА гены представляют собой последовательность номеров ИП, принимающих значения от 0 до 3. Остальная информация, относящаяся к тому или иному элементу нагрузки, не зависит от номера особи, но связана с индексом гена и используется для вычисления F. Генетический алгоритм выполняется после генерации исходной популяции и формулируется следующим образом.
1. Гены особи Z0 копируются из генов особи Z1.
2. В популяции для каждой Zi, i = 1,…,P вычисляется значение F.
3. Выполнять последующие подпункты столько раз, сколько было задано итераций.
3.1. Найти особь, у которой F максимально (наихудшую), обозначаемую ZW.
3.2. Выбрать случайным образом две особи из популяции: Zi1, Zi2.
3.3. Выполнить скрещивание особей Zi1, Zi2. Результат помещается в особь Z0. Для этого для каждого гена Z0:
3.3.1. Генерируется случайное число от 0 до 99.
3.3.2. Если это число больше процента мутаций, обозначаемого M, то новый ген с равной вероятностью копируется либо из особи Zi1, либо из Zi2.
3.3.3. В противном случае новый ген принимает случайное значение от 0 до 3, после чего проверяется наличие того или иного ИП:
3.3.3.1. Если нет ИП для Su, гену присваивается случайным образом 0, 1 или 2.
3.3.3.2. Затем, если есть ИП для Ss, но ИП для Sc нет, гену присваивается 0.
3.3.3.3. Затем, если нет ИП для Ss, но есть ИП для Sv, гену присваивается значение 2.
3.4. Вычислить F для особи Z0.
3.5. Если F(Z0) ≤ F(ZW), то особь ZW заменяется на особь Z0.
4. Найти особь, у которой минимально F. Это результат ГА.
Значения по умолчанию: P = 30, M = 20, заданное число итераций 2000000. Значения M, P можно устанавливать с использованием технологии машинного обучения, которая является подразделом искусственного интеллекта. Рассмотрим реализацию машинного обучения в рассматриваемой задаче.
Данные о результатах экспериментов по оптимизации, при которых минимально число совершенных итераций при F = 0 или достигнуто минимальное значение F, сохраняются в матрице A, состоящей из 20 строк и 40 столбцов. Каждая строка охватывает группу нагрузок, округленную до сотен часов, от 100 до 2000 часов. Если округляемое значение не округляется ни до одного значения для групп, оно заменяется ближайшим округленным значением. Каждый из первых 10 столбцов охватывает группу числа элементов нагрузки, аналогично округленную до произведений целых чисел на 5, и хранит значения рекомендуемых P. Следующие 10 столбцов аналогично используются для хранения рекомендуемых значений M, следующие 10 – аналогично для значений достигнутого числа итераций и последние 10 – соответственно для значений полученных F.
Обучение производится следующим образом. Вначале матрица заполняется нулями для первых 20 столбцов и большими значениями для последних 20 столбцов.
С целью усреднения ГА запускается с одинаковыми параметрами для одной и той же нагрузки по 10 раз. Если в матрице A в соответствующих строках и столбцах либо нулевые значения P и M, либо хранимое число итераций больше полученного, либо хранимое значение F больше полученного, все четыре значения заменяются полученными при текущей серии запусков. Затем изменяются M, P, и процесс обучения продолжается. Такие действия выполняются для разных нагрузок в целях максимального заполнения матрицы A, которая хранится в файле и может многократно открываться для продолжения обучения.
После обучения его результаты используются следующим образом. При запуске ГА выполняется поиск в первых 10 столбцах и 20 строках матрицы A ближайшего к ячейке, определяемой по размеру нагрузки и числу элементов нагрузки, непустого элемента, это значение P. Правее на 10 столбцов находится требуемое значение M. Для определения ближайшего элемента используется метрика манхэттенского расстояния.
Используемые программные средства
В ЧГУ им. И.Н. Ульянова для распределения учебной нагрузки между преподавателями используется информационная система «Кафедра» [9], в которой данные хранятся в таблицах базы данных. Само такое распределение производится построчно по усмотрению пользователя.
Для достижения цели работы разработана программа – приложение для операционной системы Windows, которая производит обработку БД системы «Кафедра». Из БД экспортируются три таблицы: NAGRPREP (годовая нагрузка, уже распределенная по преподавателям), PREPOD (сведения о преподавателях), NAGR (исходная нагрузка). Экспорт таблиц производится в формат Dbase с помощью оболочки IBExpert. Результатом оптимизации является информация о необходимости изменения значений в поле FOND таблицы NAGRPREP. Пользователь выбирает алгоритм оптимизации, устанавливает параметры, а после оптимизации переносит элементы нагрузки из одного вида в другой.
Система «Кафедра» была реализована в среде Delphi с использованием СУБД FireBird [9]. Для реализации поставленных задач используется только БД этой системы, а пользовательский интерфейс разработан с помощью среды Turbo Delphi. На рисунке изображен вид главного окна данной программы (фамилии и имена изменены).
Результаты исследования и их обсуждение
Ввиду значительного объема вычисления выполнялись с применением различных компьютеров с разной производительностью, поэтому определялось не абсолютное время работы алгоритма, а количество совершаемых итераций. Для обучения ГА параметр M изменялся от 15 до 40, P – от 30 до 60.
С целью получения более точных усредненных значений проведена оптимизация распределения ИП преподавателей кафедры компьютерных технологий за 10 лет, всего рассмотрено 225 нагрузок. Для 95 из них нагрузку не имело смысла перераспределять: все относилось к одному виду ИП. Для 32 нагрузок не удавалось получить F = 0 за длительное время; для таких ИП не проводился анализ оптимизации. В итоге при анализе учитывались 98 годовых нагрузок НПР из 225, т.е. 44%. Для каждой нагрузки проводилась оптимизация с помощью ГА по 10 раз для усреднения времени выполнения.
Среднее арифметическое времени работы ГА на настольном компьютере с процессором Intel Core i3-2120 3,3 ГГц составляет 9,62 с, максимум – 516 с. Среднее геометрическое в данном случае в 20,9 раза меньше среднего арифметического, что дает пользователю чересчур оптимистические ожидания относительно времени работы программы. Поэтому используется среднее арифметическое.
Для оставшихся вышеупомянутых 32 нагрузок в программе предусматривается разделение элементов нагрузки на части по выбору пользователя. После этого можно выполнять оптимизацию обычным образом, полагая, что полученные части – это независимые элементы нагрузки.
Заключение
Предложено использование ГА с применением машинного обучения для оптимизации распределения нагрузки преподавателя между его ИП. Программная реализация показала эффективность данного метода.