Мысленный эксперимент в физике, по сути, – одно из направлений моделирования, причем эффективное и малозатратное в смысле потребных ресурсов. При подготовке профессиональных физиков он – вкупе с математическими методами моделирования физических явлений – совершенно достаточен для достижения целей учебного познания. Однако в массовом образовании (среднем или высшем техническом) полезным подспорьем могут также быть интерактивные компьютерные модели. Обладая высоким потенциалом наглядности, они способны наилучшим образом реализовывать одну из основных функций моделей в процессе познания – иллюстративную.
Целью исследования являлось построение цикла моделей для сопровождения одного из сложных для восприятия студентами разделов курса физики – релятивистской механики – и оценка эффективности их использования на лекционных и практических занятиях.
Материалы и методы исследования
Компьютерные модели разработаны в инструментальной среде визуального проектирования и математического моделирования Stratum-2000. Использовались встроенные методы решения систем алгебраических и дифференциальных уравнений и стандартные функции визуализации. Подготовленный цикл содержит 18 моделей, из них 13 относятся к специальной теории относительности, а 5 к общей.
1. Конечность распространения светового сигнала демонстрирует модель, визуализирующая созданное одним из пары взаимодействующих тел поле и его перестройку при изменении свойств или положения этого тела. Понимание этого эффекта, так называемого дальнодействия, обычно воспринимается студентами достаточно легко.
2. Сложнее дело обстоит с эффектом относительности одновременности. В ряде учебников, например [1, 2], для представления явления используется мысленный эксперимент, описанный (вероятно, в шутку) еще Эйнштейном в одной из статей, популяризирующих специальную теорию относительности. Рассматривается движущийся поезд (или вагон), от начала и конца которого одновременно начинают распространяться навстречу друг другу световые сигналы (интерфейс соответствующей модели представлен на рис. 1, а). В неподвижной системе отсчета (на земле) наблюдатель, находившийся в момент вспышек напротив середины состава, увидит оба сигнала одновременно. А вот насчет второго наблюдателя, который находится в вагоне, также в середине состава, делается неверный вывод, что он раньше увидит сигнал, распространяющийся навстречу движению поезда, поскольку часть пути (половина состава) будет преодолена движущимся наблюдателем. Второй, «догоняющий» сигнал запоздает. Ошибка состоит в том, что, во-первых, говорить о движении второго наблюдателя «навстречу сигналу» можно не относительно поезда, а относительно земли, что и отображается на экране. Но это восприятие первого наблюдателя.
Во-вторых, в соответствии со вторым постулатом теории относительности скорость света в вакууме одинакова во всех системах отсчета, и, значит, в движущейся системе сигналы от концов поезда дойдут до его середины за одинаковое время. «Правильная» визуализация эффекта относительности одновременности (рис. 1, б) соответствует изложению в [3, 4].
3. Инвариантность поперечных длин иллюстрируется (рис. 2) посредством изображения в двух системах отсчета тел (карандашей), оставляющих при движении следы (цветные линии), позволяющие сопоставлять размеры тел. Предположение, что поперечные длины при движении изменяются, приводит к противоречию: в одной системе отсчета короче желтый карандаш, в другой – красный, но объективно соотношение уровня нарисованных линий в обеих системах отсчета одинаково (доказательство от противного).
4. Эффект замедления времени представлен в нашем цикле тремя моделями. Первая из них имеет аналоги в других программных продуктах: рассматривается поперечное по отношению к движению платформы распространение светового импульса (фотона) от источника до зеркала и обратно в системах отсчета, связанных с платформой и с землей (рис. 3, а).
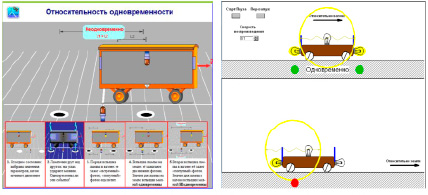
а б
Рис. 1. Иллюстрация эффекта относительности одновременности – лампа вспыхивает, принимая сигнал: а) ошибка: фактически изображение воспринимается относительно земли; б) корректно: процесс распространения световой волны рассматривается в двух системах отсчета
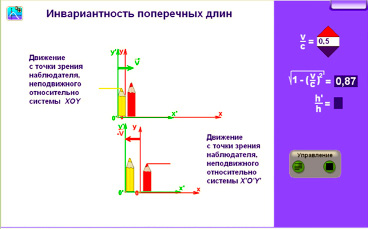
Рис. 2. Инвариантность поперечных длин: сделано предположение, что движущийся карандаш становится короче, тогда в верхнем окне красная линия выше желтой, а в нижнем – наоборот
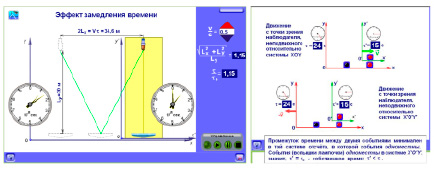
а б
Рис. 3. Эффект «замедления времени»: а) время движения больше в системе отсчета, в которой больше пройденный светом путь; б) критерий: одноместные события и собственное время
Поскольку вертикальная составляющая движения фотона в обеих системах отсчета одинакова, скорость света – инвариант, а путь, пройденный фотоном относительно земли, больше, то время движения в системе отсчета, связанной с землей, больше, чем в системе отсчета, связанной с платформой. При этом учащихся может ставить в тупик вопрос: в соответствии с принципом относительности движения каждая система отсчета движется относительно другой – так в какой системе время должно течь медленнее, если и ту и другую можно рассматривать как движущуюся?
Лучшее понимание эффекта обычно появляется при анализе еще двух зеркально дополняющих друг друга моделей, поясняющих отличие в процедуре измерения промежутка времени в двух системах отсчета. В одной системе отсчета на некотором фиксированном расстоянии установлены две лампочки; во второй системе одна. Часы в обеих системах включаются, когда становятся равны продольные по отношению к движению координаты первой пары лампочек в движущейся и неподвижной системах отсчета; часы выключаются (рис. 3, б), когда становятся равны координаты второй пары. События включения и выключения часов в штрихованной системе отсчета одноместны; время в этой системе называется собственным, продолжительность процесса здесь минимальна (время течет медленнее).
5. Эффект сокращения продольных длин также иллюстрируется тремя моделями. Лампочки с рис. 3, б, служат концами стержня, длина которого измеряется как произведение скорости относительного движения систем отсчета на продолжительность движения «одинокой лампочки мимо стержня» по часам каждой из систем. В той системе, часы которой измеряют собственное время, продолжительность движения и, значит, длина стержня меньше. Для второй же системы характерно то, что стержень относительно нее неподвижен. В этом случае длина стержня называется собственной. Таким образом, собственная длина стержня имеет максимальную величину, а в системах отсчета, относительно которых стержень движется, его длина уменьшается.
Для одномерных тел (стержней) цикл содержит две зеркально дополняющие друг друга модели (к штрихованной или нештрихованной системе привязан стержень), которые, как и для эффекта замедления времени, дают одинаковый результат. Третья модель демонстрирует изменение при движении соотношения сторон прямоугольного тела и угла между его диагоналями.
Фиксация «экспериментальных» соотношений
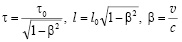
позволяет при получении преобразований координат, аналогичных галилеевским, учесть сокращение длин и замедление времени как поправки к классической ситуации и прийти к формулам преобразований Лоренца для координат, релятивистскому закону сложения скоростей и далее – доказать предельный характер скорости света.
Таким образом, реализуется вариант изложения релятивистской механики с опорой на модельный эксперимент, что имеет свои плюсы при обучении инженеров. Хотя, разумеется, этот «эксперимент» имеет смысл лишь иллюстрации эффектов, а фундаментальные реальные эксперименты позволили в свое время сформулировать постулаты теории относительности.
6. Четырехмерное пространство Минковского, представляемое в виде пары световых конусов, – само по себе уже модель, позволяющая, c одной стороны, говорить о едином пространственно-временном континууме, а с другой, подчеркивать отличие между времениподобными и пространственноподобными интервалами, причинно связанными и причинно несвязанными событиями [5]. Компьютерная модель визуализирует эту абстракцию, позволяет построить мировые линии для имеющих массу тел, движущихся с различными скоростями (или покоящихся), а также мировые линии для фотонов, лежащие на поверхности конусов.
7. Предельный характер скорости света иллюстрируется моделью цикла, в которой параметрами являются масса рассматриваемого тела и действующая на него сила. Ведется расчет и строятся графики зависимости от времени для импульса, кинетической и полной энергии, ускорения и скорости тела. При действии постоянной силы импульс растет линейно, ускорение в релятивистском диапазоне падает, график скорости тела выходит на горизонтальную асимптоту, соответствующую скорости света. В ультрарелятивистской области совершаемая внешней силой работа идет, как и в классической физике, на увеличение импульса и энергии, но без существенного роста скорости.
8. Следующая модель (рис. 4) позволяет имитировать опыты Кауфмана (1902 г.), в которых была обнаружена «зависимость массы» электрона от его скорости (в настоящее время масса понимается как постоянная характеристика тела, но релятивистский импульс определяется через нелинейную функцию скорости).
Модель позволяет изменять скорость частицы и индукцию магнитного поля, влетая в которое электрон движется по траектории, представляющей собой полуокружность. Измерение продолжительности этого движения и, соответственно, периода вращения позволяет рассчитать «классические» значения импульса и радиуса круговой траектории, в то время как модель использует для расчета релятивистские формулы. Графики зависимости от скорости для релятивистского импульса, для его отношения к рассчитанной классическим способом величине импульса, а также для удельного заряда электрона демонстрируют радикальное расхождение «экспериментальных» зависимостей с классическими представлениями. Все три зависимости нелинейны и имеют выраженные асимптоты.
9. Моделей, иллюстрирующих эффекты, относящиеся к общей теории относительности, в цикле представлено пять.
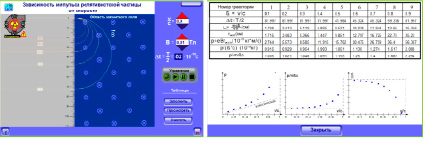
Рис. 4. Имитация опыта Кауфмана: окна интерфейса модели и расчетных таблиц и графиков
Две из них (по сути, это анимации) демонстрируют эквивалентность действия гравитации и движения в неинерциальной системе отсчета на ход часов и на движение частицы.
Две трехмерные модели призваны создать наглядный образ искривленного гравитирующим телом пространства и его действия на распространение света. Искажение пространства отображается не буквально, а в образной форме. Пространство изображено двумерным, в виде плоскости, пронизанной сеткой с квадратными ячейками. Ячейки квадратны вдали от массивного шара, но деформируются в непосредственной близости от него. Этот эффект хорошо виден при «взгляде сверху» (камера может перемещаться). Третье измерение, перпендикулярное сетке, нефизическое: оно, как и ячейки, лишь создает образ воздействия гравитации на свойства пространства, визуализируя интенсивность этого воздействия. Наблюдать за «изменением степени искривления пространства» можно, изменяя массу тела и перемещая его по плоскости. Вторая модель отображает распространяющийся в той же системе свет как частицу, движущуюся по поверхности «продавленной» сетки, вследствие чего нарушается прямолинейность.
Еще одна модель иллюстрирует аномальное (более быстрое, чем соответствует классическому описанию) смещение перигелия, обнаруженное для Меркурия в середине XIX в. Эффект не мог быть объяснен законами механики Ньютона. В общей теории относительности он объясняется влиянием гравитации на свойства пространства-времени – его геометрия заметно отличается от евклидовой. В модели эффект визуализируется путем построения траектории тела, которая близка к эллиптической, но является незамкнутой; расчет ведется, разумеется, по законам классической механики, но с искусственно внесенной погрешностью.
Результаты исследования и их обсуждение
Описанный выше цикл моделей входит в состав компьютерной обучающей среды «Интер@ктивная физика», разработанной под методическим руководством автора и распространяемой «Институтом интеллектуальных технологий» (г. Пермь). Программный продукт более десяти лет используется в 600 учебных заведениях Пермского края и других регионов. Методическая поддержка продукта автором и организацией-разработчиком осуществляется в том числе путем проведения курсов повышения квалификации преподавателей физики (более 700 чел. за 7 лет в Пермском крае, а также в Республике Татарстан, Республике Коми).
Описанный выше цикл моделей в течение ряда лет использовался автором на лекциях при изложении основ релятивистской механики студентам Пермского национального исследовательского политехнического университета. С целью повышения наглядности, направленного формирования представлений и освоения понятий курс физики сопровождается большим числом интерактивных модельных демонстраций, призванных создавать визуальную основу для лучшего восприятия и осмысления учебного материала.
Эффективность используемой методики показывают ежегодные срезы знаний в форме письменных работ, предполагающих как изложение теоретических вопросов с интерпретацией экспериментальных данных, так и решение задач. В экспериментальных группах доля работ, оцениваемых на «хорошо» и «отлично», обычно превышает 70 %, в то время как в контрольных группах, где занятия проводятся в рамках «меловой физики» (по чисто техническим причинам), едва достигает 50 %. Тенденция к улучшению понимания студентами учебного материала заметна также в ходе бесед с ними при сдаче индивидуальных подборок задач.
Таким образом, есть основания утверждать, что описанные модели не только визуализируют изучаемые эффекты, но позволяют более доходчиво их объяснять и, что особенно важно, способствуют освоению учащимися новых действий, например осознанного выполнения процедур измерения промежутков времени и расстояний в различных системах отсчета, что отнюдь не тривиально в ситуации движения тел с релятивистскими скоростями. Впоследствии эти умения оказываются востребованы при работе с реальными техническими устройствами, например, для студентов направления «Фотоника и оптоинформатика» – с оптоволоконными гироскопами, принцип действия которых основан на эффекте Саньяка.
Заключение
Освоение понятийной базы нового раздела учебной дисциплины всегда требует от учащихся значительных усилий, даже если это касается тем, непосредственно связанных с повседневной жизнью, например движения тел в случае физики. Наряду с бытовыми понятиями и представлениями о движении, которые формируются интуитивно, встречаются весьма абстрактные понятия и представления, такие, например, как векторный характер физических величин или относительность движения. Еще большие сложности для понимания возникают в ситуациях, когда тела движутся с релятивистскими скоростями и бытовые представления оказываются некорректными. Проведенное исследование показало, что для значительной части учащихся представленный цикл моделей позволяет существенно повысить уровень понимания и качество освоения учебного материала.



