Функциональная МРТ (фМРТ) – метод картирования коры головного мозга, позволяющий определять индивидуальное местоположение и особенности областей мозга, отвечающих за движение, речь, зрение, память и другие функции, индивидуально для каждого пациента. Суть метода заключается в том, что при работе определенных отделов мозга кровоток в них усиливается. В процессе проведения фМРТ пациенту предлагается выполнение определенных заданий, участки мозга с повышенным кровотоком регистрируются, и их изображение накладывается на обычную МРТ мозга [1].
Несомненно, факт человеческой ошибки при определении различных патологий головного мозга крайне велик, поскольку при сканировании методом МРТ генерируется значительное количество снимков (информации). Человек не всегда способен уловить малейшие отклонения, возникающие на снимках ввиду высокой сложности и разнообразности таких отклонений и их свойств.
С учетом все большего накопления цифровых данных в этой области, а также поступательного развития современных графических процессоров становится возможным применение методов машинного и глубинного обучения для построения различного рода предсказательных моделей поведения головного мозга. Более того, данные методы зачастую показывают гораздо более высокую эффективность и точность предсказаний по сравнению с теми решениями, которые принимаются человеком [2, с. 64–72], в том числе путем ручной классификации [3].
Материалы и методы исследования
В рамках исследования использованы следующие открытые наборы данных: HCP [4], ABIDE I [5].
Датасет HCP содержит 1113 наборов данных от людей со структурными МРТ. Данные представлены от 507 мужчин и 606 женщин. Датасет был преобразован в трехмерные изображения размером 58х70х58 точек из размера 260х311х260 точек. Данное преобразование было реализовано с целью сокращения потребления имеющихся ресурсов графических процессоров, а также в целях получения лучшего по сравнению с исходным изображением результата классификации, поскольку меньший размер входного изображения обеспечивает большее воспринимающее поле для модели CNN. Для масштабирования был использован функционал библиотек DIPY и SciPY. Для визуализации данных использовалась библиотека nilearn.
Датасет ABIDE I содержит 1093 набора данных людей, подвергшихся периодическому контролю, в возрасте от 7 до 64 лет. Кроме того, представлены данные о гендерной принадлежности снимка головного мозга. Также следует отметить, что данный датасет является несбалансированным (количество мужчин и женщин 932 и 161 соответственно).
В качестве функции потерь в модели классификации была использована nn.NLLLoss, входными данными для которой являются вектор логарифмической вероятности и метка цели; в модели регрессии – nn.L1Loss, которая считает среднюю абсолютную ошибку (MAE) между каждым предсказанным значением и истинным.
В качестве оптимизатора применялся optim.Adam с гиперпараметром lr = 3e-4.
Также в процессе обучения использовался scheduler – MultiStepLR, который понижал значение гиперпараметра lr оптимизатора на 0.1 каждые n эпох.
Метриками качества для модели классификации являлись точность (Accuracy) между предсказанным и истинным классом и roc_auc_score.
Для модели регрессии использовалась метрика средней абсолютной ошибки (MAE).
Для визуализации полученных результатов использовалась библиотека matplotlib.
Результаты исследования и их обсуждение
Архитектура сверточных нейронных сетей, используемых в моделях классификации и регрессии, представлена на рис. 1, 2 соответственно.
Как становится видно по рисункам, нейросети отличаются лишь последней частью. В случае с регрессией используются 3 линейных слоя, а в случае классификации – линейный слой и функция softmax.
Для более глубокого понимания опишем слои, из которых состоит нейросеть.
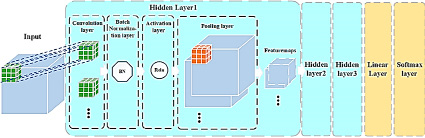
Рис. 1. Архитектура сверточной нейронной сети, используемой в модели классификации
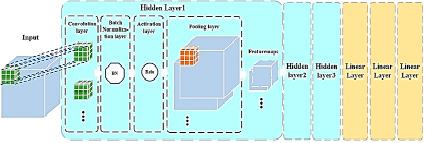
Рис. 2. Архитектура сверточной нейронной сети, используемой в модели регрессии
Сверточный слой
Процесс работы сверточного слоя представляет свертку входного вектора I со сверткой ядра K, представленного I ⊗ K. Форма входного вектора в нашей 3D-модели CNN представляет собой [n, d, w, h, c], где d, w, h, c – глубина, ширина, высота и номера каналов входного вектора, соответственно, а n – размер пакета (гиперпараметр, который был подобран эмпирическим путем и составляет 45). В первом слое входной размер составлял 58 × 70 × 58 × 1, что представляло собой трехмерное объемное изображение (58 × 70 × 58) в градациях серого. Форма ядра свертки представляет собой [d k, w k, h k, c in, c out], где d k, w k, h k – глубина, ширина и высота ядра свертки соответственно (во всех трех скрытых слоях размер ядра был установлен 3 × 3 × 3, что означает, что d k = w k = h k = 3); c in – количество входных каналов, равное номеру входного канала; c out – количество ядер свертки, а также количество входных каналов для следующего скрытого слоя. Во всех слоях свертки шаг движения ядра был установлен в размере 1, а режим заполнения – «SAME».
Слой батч-нормализации
После сверточного слоя каждый мини-пакет (mini-batch) нормализовался с нулевым средним и единичной дисперсией в скрытых слоях сети в целях облегчения явления градиентного внутреннего ковариантного сдвига и ускорения обучения нейронной сети, для которого использовался метод Adam Gradient Descent.
Слой активации
После операции нормализации была использована функция активации ReLU для нелинейной обработки результата свертки.
Пуллинговый слой
Слой pooling layer был добавлен после слоя активации. Слои объединения в нейронной сети суммируют выходы соседних групп нейронов в одной и той же карте ядра. В этом слое использовался метод максимального объединения.
Выходные данные предыдущего скрытого слоя являлись входами для следующего уровня. В нашей модели первый скрытый слой сгенерировал 32 feature maps, второй скрытый слой – 64, а третий – 128. Наконец, в рамках исследования последние 128 feature maps были интегрированы через линейный слой во входные данные слоя softmax, который и выдавал окончательные результаты классификации.
В конце каждого скрытого слоя был добавлен слой Dropout c параметром 0.2 (получен эмпирически), который в ходе обучения модели случайным образом занулял входные данные с вероятностью p = 0.2, что благоприятно сказывалось на работе модели без потери качества.
Линейный слой
Слой в нейронной сети, который выполняет линейные преобразования по формуле
y = x × AT + b.
Summary полученных моделей представлено на рис. 3.
В рамках исследования было проведено 11 экспериментов, в том числе 8 для классификации и 3 для регрессии. Все эксперименты проводились с разбиением на тренировочную и тестовую выборки в размере 80 и 20 % от датасета, соответственно. Количество эпох обучения – 20 для классификации, 25 – для регрессии. Параметры экспериментов и полученные результаты представлены ниже.
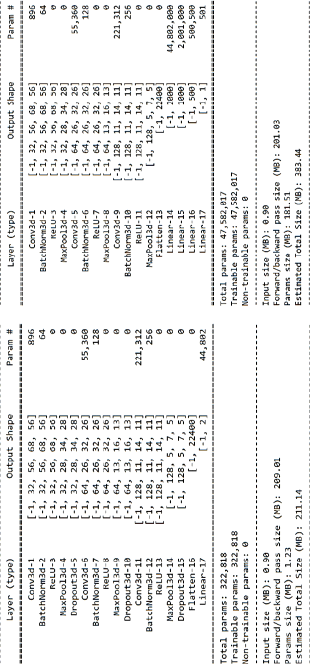
Рис. 3. Summary полученных моделей классификации и регрессии
Параметры эксперимента № 1 для классификации:
− датасет: HCP;
− метрика: Accuracy.
Полученные результаты на train и test представлены на рис. 4.
Значение точности при тройной кросс-валидации: 89,757.
Параметры эксперимента № 2 для классификации:
− датасет: HCP;
− метрика: roc_auc_score.
Полученные результаты на train и test представлены на рис. 5.
Резюмируя результаты, отраженные в рис. 4 и 5, можно сделать однозначный вывод о поступательном снижении ошибки, начиная с первой итерации. При этом можно отметить, что на первой итерации модель неверно трактовала метки класса, а начиная со второй итерации, значения ошибки и метрики качества близятся к сходимости (значения Loss близки к 0,25, значения accuracy и roc_auc_score – к 0,9).
Параметры эксперимента № 3 для классификации:
− датасет: ABIDE I (несбалансированная выборка);
− метрика: Accuracy.
Полученные результаты на train и test представлены на рис. 6.
Значение точности при тройной кросс-валидации: 90,027.
Параметры эксперимента № 4 для классификации:
− датасет: ABIDE I (несбалансированная выборка);
− метрика: roc_auc_score.
Полученные результаты на train и test представлены на рис. 7.
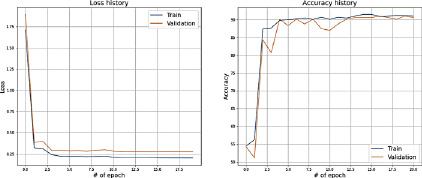
Рис. 4. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
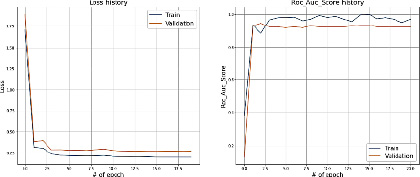
Рис. 5. Значения Loss и ROC_AUC_SCORE при сплите датасета в 80 и 20 %
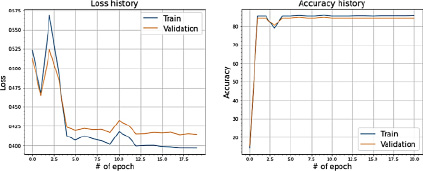
Рис. 6. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
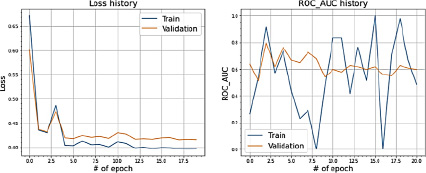
Рис. 7. Значения Loss и ROC_AUC_SCORE при сплите датасета в 80 и 20 %
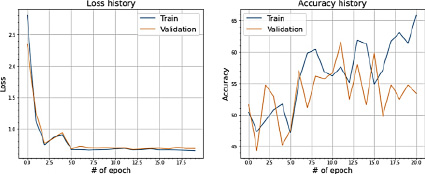
Рис. 8. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
Рисунки 6 и 7 характеризуют несбалансированный характер датасета ABIDE I. Как мы видим из метрики ошибки, сходимость достигается не после первой итерации. Более того, сами значения близки к 0,5, а в более поздних итерациях – к 0,4, что говорит о том, что модель не может с высокой точностью определять верную метку классификатора. Метрика качества accuracy ведет себя стабильнее, достигая стабильных значений около 0,9. Метрика roc_auc_score ведет себя непредсказуемо, особенно на этапе обучения модели.
Параметры эксперимента № 5 для классификации:
− датасет: ABIDE I (с применением sampler);
− метрика: Accuracy.
Полученные результаты на train и test представлены на рис. 8.
Параметры эксперимента № 6 для классификации:
− датасет: ABIDE I (с применением sampler);
− метрика: roc_auc_score.
Полученные результаты на train и test представлены на рис. 9.
Искусственное создание дополнительных сэмплов для придания выборке сбалансированности к положительному результату не приводит. Данный факт подтверждается рис. 8 и 9.
И метрики ошибки, и метки качества ведут себя более непредсказуемо, чем без искусственного сэмплирования. Дисперсия увеличивается.
Далее было проведено несколько экспериментов с переносом весов соответствующих моделей, обученных на классификации датасета HPC, для классификации датасета ABIDE I.
Параметры эксперимента № 7 для классификации:
− датасет: ABIDE I (c переносом весов);
− метрика: Accuracy.
Полученные результаты на train и test представлены на рис. 10.
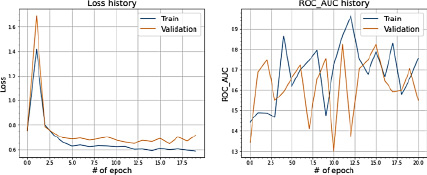
Рис. 9. Значения Loss и ROC_AUC_SCORE при сплите датасета в 80 и 20 %
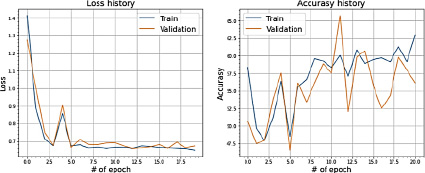
Рис. 10. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
Параметры эксперимента № 8 для классификации:
− датасет: ABIDE I (c переносом весов);
− метрика: roc_auc_score.
Полученные результаты на train и test представлены на рис. 11.
Применение методики переноса весов от сбалансированной модели к желаемому результату не привело.
Сходимость ошибки в обоих случаях останавливается около 0,65. При этом качественные метрики в основном находятся в коридоре от 0,4 до 0,7. Сходимости не наблюдается. Дисперсия остается значительной.
Данные выводы отражены на рисунках 10 и 11.
Параметры эксперимента № 9 для регрессии:
− датасет: HCP;
− метрика: MAE.
Полученные результаты на train и test представлены на рис. 12.
Параметры эксперимента № 10 для регрессии:
− датасет: ABIDE I;
− метрика: MAE.
Полученные результаты на train и test представлены на рис. 13.
Параметры эксперимента № 11 для регрессии:
− датасет: ABIDE I (с переносом весов);
− метрика: MAE.
Полученные результаты на train и test представлены на рис. 14.
На рис. 12–14 отчетливо прослеживается схожесть поведения метрик ошибки и качества. Сходимость обоих показателей стремится к уровню ниже 3, что означает, что разница между предсказанием моделью возраста пациента и фактическим значением не превышает трех лет. Также по результатам экспериментов выявлено, что сходимость несбалансированного датасета ABIDE I с увеличением итераций происходит без особого увеличения дисперсии.
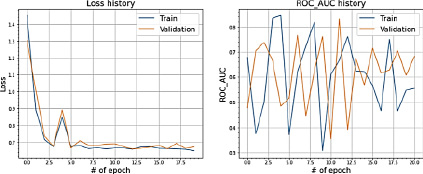
Рис. 11. Значения Loss и ROC_AUC_SCORE при сплите датасета в 80 и 20 %
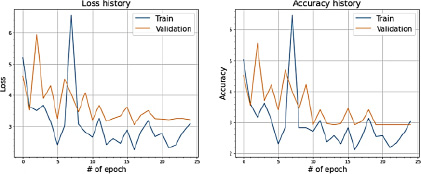
Рис. 12. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
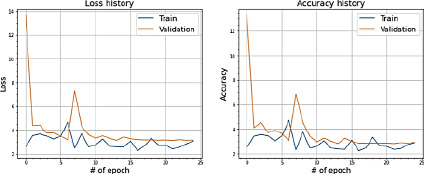
Рис. 13. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
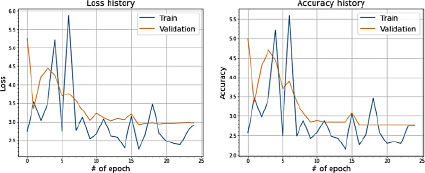
Рис. 14. Значения Loss и Accuracy при сплите датасета в 80 и 20 %
Таким образом, можно сделать вывод, что признаки для регрессионного анализа в данном датасете выражены в большей по сравнению с датасетом HCP степени.
Заключение
По результатам проведенных экспериментов можно сделать следующие выводы.
Для датасета HCP (задача классификации): модель показывает стабильную работу и стабильные значения точности, правильно классифицируя около 90 % сэмплов. Предсказаниям такой модели можно доверять с высокой степенью вероятности и достоверности.
Для датасета ABIDE I (задача классификации): Значения функции потерь значительно выше, чем у датасета HCP. Кривые ROC_AUC_SCORE показали очень нестабильные результаты, связанные с попаданием в тренировочные данные сэмплов лишь одного класса. Искусственная балансировка классов, как и перенос весов модели с датасета HCP, к видимым результатам не привели. Из чего можно сделать вывод, что предсказания такой модели, в том числе отбалансированной, не являются достоверными.
При проведении экспериментов для регрессии средняя ошибка модели для датасета HCP cоставила 2,8 года, для датасета ABIDE I – 3 года. Перенос весов сократил ошибку до 2,7 года. При этом стоит отметить более быструю обучаемость модели и сходимость ошибки, что благоприятно отражается на затрачиваемых ресурсах.
Высокая точность классификации датасета HCP, который является заранее сбалансированным, позволяет утверждать, что в структуре мозга мужчины и женщины есть существенные различия, которые уверенно может находить сверточная нейронная сеть.
Несбалансированность данных в датасете ABIDE I подтверждает факт ухудшения полученных результатов при поиске различий в структуре мужского и женского мозга, что говорит о важности предобработки и подготовки исходных данных для решения обсуждаемого в статье спектра задач.
В задаче предсказания возраста по трехмерным снимкам фМРТ предложенная модель показала себя уверенно на обоих наборах данных, что опять же подтверждает факт возможности использования нейросетей в рамках поднятой проблематики, а также отсутствие важности сбалансированности классов при решении именно задачи регрессии, когда классифицирующие признаки не являются значимыми.



