Первичные трещины в металлах исследованы в работах [1, 2]. Было показано, что их длина составляет в среднем доли микрона. Однако позже в работе [3] было обнаружено, что первичные трещины в твердых телах возникают в наносекундном диапазоне и длина их составляет нанометры. Так появился термин нанотрещина, который был связан с толщиной поверхностного слоя твердого тела [4]. Для металлов длина нанотрещины составляет 2–4 нм, и через 100 нс она превращается в мезотрещину, рост которой достигает микрона [4]. Длина нанотрещины пропорциональна молярному объему элемента: Lnm = 0,17∙10-9υ, и для металлов она зависит от порядкового номера Z в таблице Д.И. Менделеева (рис. 1, а). На рис. 1, б, показана зависимость поверхностной энергии γ от температуры плавления Tm: γ = 7,8∙10-4 Tm , полученная эмпирически в работе [5].
В настоящей работе мы рассмотрим поведение нанотрещины в упрочняющем покрытии TiN, нанесенном ионно-плазменным методом на сталь 20Х13.
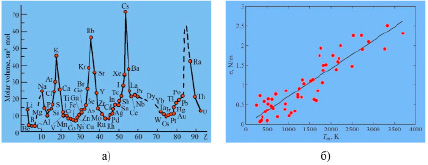
Рис. 1. Периодическое изменение молярного объема элементов (а); коррелятивная зависимость поверхностной энергии от температуры плавления (б) [5]
Таблица 1
Химический состав стали 20Х13
|
C |
Si |
Mn |
Ni |
S |
P |
Cr |
Fe |
|
0,16–0,25 |
до 0,6 |
до 0,6 |
до 0,6 |
до 0,025 |
до 0,03 |
12–14 |
~ 84 |
Таблица 2
Физические параметры стали 20Х13
|
Сталь |
Lnm = R(I), нм |
Tm, К |
γ, Дж/м2 |
γ1, Дж/м2 |
|
20Х13 |
1,21 |
1820 |
1,420 |
0,473 |
Первичные трещины в стали 20Х13
Первичные нанотрещины твердого тела возникают при образовании его поверхности из-за ее реконструкции или релаксации. При этом возникают напряжения в поверхностном слое, приводящие к возникновению дислокаций, дефектов упаковки и т.д. и, следовательно, нанотрещин Lnm. Размер поверхностного слоя R(I) определен нами в работе [6]:
Lnm = 0,17∙10-9 υ. (1)
Уравнение (1) определяет параметр – атомный объем металла или его сплава, равный υ = М/ρ (М – молярная масса, ρ – ее плотность). Химический состав стали 20Х13 показан в табл. 1.
Для твердых растворов примем следующие соотношения:
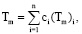
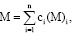
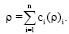 (2)
(2)
В [5] показано, что поверхностная энергия объемного металла γ с точностью до 3 % равна
γ = 7,8∙10-4 Tm, (3)
где Tm – температура плавления металла (К).
В слое R(I) нужно учесть размерный эффект, и энергия слоя R(I) становится равной γ1 [7]:
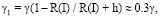 . (4)
. (4)
Уравнение (4) показывает, что энергия слоя R(I) в три раза меньше энергии основного металла. Используя (1)–(4), приведем параметры стали 20Х13 в табл. 2.
Осаждение покрытия TiN и ее адгезия
Покрытия нитрида титана на турбинные лопатки паровой турбины Т-100/120-130-2 ТМЗ наносились ионно-плазменным методом на установке ННВ-6.6И1 (рис. 2, а). На рис. 2, б, показан переходной слой между сталью и нитридом титана, измеренном на сколе турбинной лопатки на электронном микроскопе MIRA 3 фирмы TESCAN. Толщина переходного слоя оказалось равной около 0,13 мкм.

Рис. 2. Турбинные лопатки с нитрид-титановым покрытием (а); переходной слой (б)
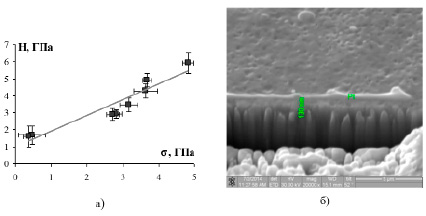
Рис. 3. Зависимость микротвердости от величины сжимающих остаточных напряжений в покрытии TiN на сталь 12Х18Н10Т (а) [9]; толщина переходного слоя (б)
Длина трещин идет по схеме:
Lnm → Lµm = 102 Lnm,
т.е. из табл. 1 следует, что длина мезотрещин равна Lµm = 0,121 мкм, что не сильно отличается от толщины переходного слоя. Вверху этого слоя находится TiN, а внизу – сталь 20Х13.
Чтобы отделить покрытие TiN от стали, нужно затратить работу, которая называется работой или энергией адгезии и дается выражением типа Дюпре [8]:
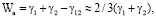 (5)
(5)
где γ1 = 2,510 Дж/м2 – поверхностная энергия TiN, γ2 = 1,420 Дж/м2 – поверхностная энергия стали 20Х13, γ12 ≈ 1/3γ1 + 1/3γ2 – поверхностная энергия переходного слоя.
Энергия адгезии равна: Wa = 2,620 Дж/м2. Напряжения в переходном слое равно σа [8]:
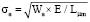 , (6)
, (6)
где Е = 236 ГПа – модуль Юнга переходного слоя.
В результате мы получили:
σа = 2260 МПа.
Эти напряжения, связанные с переходным слоем в покрытии, следует трактовать как остаточные напряжения. Они связаны с релаксацией поверхности стали 20Х13. Какова же твердость переходного слоя? На этот вопрос можно ответить рис. 3, а, взятым из работы [9], где TiN наносился на сталь 12Х18Н10Т.
На рис. 3, б, показана толщина переходного слоя покрытия, полученного с использованием системы Quanta 200 3D, которая совмещает в себе сканирующий электронный микроскоп с термоэмиссионным катодом, сфокусированный ионный пучок, позволяющий прецизионно наносить и удалять материалы. Переходной слой отделялся от TiN и стали 20Х13 слоем из платины Pt.
Из рис. 3, а, из значения σа следует, что твердость переходного слоя Н ≈ 3000 МПа. Для определения нанотвердости полученных покрытий нами использовалась зондовая лаборатория Ntegra с индентором Берковича. Для покрытия TiN эта величина оказалась равной HTiN ≈ 21000 МПа, что в 7 раз больше Н переходного слоя. Сделаем теперь некоторые сравнения.
У стали 20Х13 в виде закаленного прутка предел прочности σВ = 830 МПа [10], что в 25 раз меньше HTiN, значит, у стали идет упрочнение. Для покрытий TiN предел прочности изменяется от 16000 до 30000 МПа в зависимости от способа осаждения покрытий. У литых высокопрочных сталей предел прочности составляет около 1700 МПа, у поковок высокопрочных сталей предел прочности несколько ниже, около 1200 МПа, у высокопрочных низколегированных сталей – 550 МПа [10].
Полученную величину H ≈ 3000 МПа следует назвать адгезионной прочностью нитрид-титанового покрытия на турбинную лопатку из стали 20Х13.
Адгезионная прочность покрытий бронз, полученных на стали 45 методом деформационного плакирования, составила в среднем 15 МПа [11]. В работе [12] исследовалась адгезионная прочность покрытий Ti-Hf-Si-N на стали 3. На рис. 4, а, показана схема установки для проведения эксперимента по измерению адгезионной прочности покрытия. Суть эксперимента заключалась в следующем: определялись критические нагрузки: во-первых, начало проникновения индентора в покрытие; во-вторых, когда появляется первая трещина; в-третьих, когда происходит отслаивание в некоторых участках покрытия; в-четвертых, когда покрытие истирается до стальной основы.
На рис. 4,б, показана нанотвердость покрытия НTiHfSiN = 42700 МПа с индентором Берковича вместо HTiN ≈ 21000 МПа, полученного в нашем покрытии. Результатом работы [12] является тот факт, что адгезионное разрушение покрытия TiHfSiN на стали 3 наблюдается при 9,81 Н. Это соответствует параметру А1 = H3/Е2 = 0,51 ГПа (при H = 42,7 ГПa и E = 390 ГПа). В нашем случае А2 = H3/E2 = 0,25 ГПа (при HTiN ≈ 21 ГПа и E = 336 ГПа). Это соответствует отношению А1 / А2 = 2 или НTiHfSiN / HTiN ≈ 2, т.е. покрытие TiHfSiN в 2 раза прочнее, чем покрытие TiN.
Однако выше мы отметили: полученную величину переходного слоя H ≈ 3 ГПа следует назвать адгезионной прочностью нитрид-титанового покрытия на турбинную лопатку из стали 20Х13. Именно в этом слое происходит отделение прочного покрытия от непрочной стали. И именно этот переходной слой формируется за счет первичных трещин, которые характерны для стали 20Х13.
На сегодняшний день существуют несколько теорий адгезии, включающие механическую, диффузионную, электронную, адсорбционную, релаксационную и слабого слоя на границе [8]. Механическая теория адгезии была предложена Мак-Беном, согласно которому она осуществляется путем затекания адгезива в трещины на поверхности субстрата с последующим его затвердеванием (рис. 5, а). В нашем случае адгезивом служит покрытие TiN, которое осаждается с помощью плазмы и затекает в трещины, остывая в субстрате. Значит, мы имеем механический вариант теории адгезии. Диффузионная теория адгезии, впервые предложенная Воюцким, рассматривает диффузию адгезива в структуру субстрата (рис. 5, б). В нашем случае происходит диффузия ионов осаждаемого металла внутрь стали. Значит, мы также имеем диффузионный вариант адгезии.
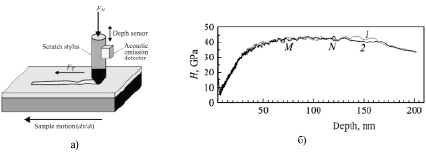
Рис. 4. Схема экспериментальной установки для определения адгезионной/когезионной прочности. FN – величина нормальной нагрузки, FT – сила трения (а); зависимости твердости H от глубины вдавливания (б). Точками отображаются места, где проводились измерения H. Кривые 1 и 2 соответствуют разным измерениям для одного и того же образца. Светлые точки на части c – места измерений для кривой 1, темные точки – места измерений для кривой 2 [12]

Рис. 5. Механическая (а) и диффузионная (б) теории адгезии [8]

Рис. 6. Электронная (а) и релаксационная (б) теории адгезии [8]
Электронная теория адгезии была создана Дерягиным и Кротовой. В ее основе лежит электрический конденсатор, обкладки которого представляют адгезив и субстрат (рис. 6, а). В нашем случае мы имеем покрытие TiN, нанесенное на сталь 20Х13, которое также можно рассматривать как конденсатор с различными обкладками, внутри которого находится поверхностный слой. Затронем также релаксационную теорию адгезии, которая рассматривает процессы деформации, обусловленные внутренними напряжениями (рис. 6, б). Релаксационная теория адгезии занимает в нашем рассмотрении ведущую роль.
В настоящей статье обоснован новый подход к адгезии покрытий на металл, связанный с наноструктурой поверхностного слоя и первичными трещинами, возникающими от внутренних напряжений в переходном слое из-за эффекта релаксации поверхности.
Адгезионная прочность различных покрытий и соединений продолжает оставаться предметом различных способов определения [13] и дискуссий [14].
Заключение
Имеются стандарты – ГОСТ 9.302-88 и другие. Большинство из этих ГОСТ (методов) не включают структуру поверхностного слоя, который возникает за счет диффузионных процессов при нанесении покрытий. В настоящей статье впервые предложена структура поверхностного слоя, обусловленная первичными трещинами, через которые и происходит диффузия осаждаемых компонет. Первичные нанотрещины металла отображают его атомную структуру, и через 100 нс они превращаются в мезотрещины, формируя поверхностный слой. Чтобы разрушить этот слой, необходимо совершить работу адгезии. Окончательно адгезионную прочность покрытия можно определить теоретически, используя предложенные в статье формулы и экспериментально определяемые свойства покрытий и основы, на которую осаждаются покрытия.
Данная научная статья опубликована в рамках выполнения научной программы программно-целевого финансирования на 2021–2023 гг. ИРН № BR1090150221 «Разработка технологии защитных покрытий поверхностей вооружения и военной техники для защиты от агрессивных факторов окружающей среды и условий эксплуатации» (исследование финансируется Комитетом науки Министерства науки и высшего образования Республики Казахстан).



