Социально-экономические системы (СЭС) в условиях рынка являются открытыми, неравновесными и активно взаимодействующими друг с другом экономической, социальной, экологической и т.д. подсистемами. Обмен финансами, ресурсами, информацией приводит, как правило, к изменению параметров систем, например социальной структуры, производственных и трудовых ресурсов, что ведёт к неустойчивости СЭС. Этот процесс иногда приводит к структурным изменениям и образованию новой организации и способа функционирования систем [1-3]. Для изучения прогнозов изменений в СЭС естественно использование различных математических методов [4-6]. Одним из них является метод имитационных динамических моделей, основанный на использовании систем обыкновенных дифференциальных уравнений для описания основных переменных. Однако число уравнений, необходимое для описания СЭС, достигает десятки и сотни. Совокупность уравнений и соотношений, связывающих сложные комплексы экономических, социальных и политических взаимоотношений в обществе, а также описание взаимодействия общества с окружающей средой и другими СЭС составляют искомую имитационную модель. В современном мире многие государства являются федеративными республиками, имеющими свои законы, налоги и правительства. Потому следует считать динамические модели СЭС как систему социально-экономических структур [5; 7; 8].
В характере развития СЭС, наряду с эволюционным развитием, возникают процессы катастрофических, хаотических, революционных изменений, сопровождающихся сменами социальных структур и систем управления. Как правило, катастрофические изменения различных типов, приводящие к хаосу, в последующие моменты переходят к самоорганизации новых оптимальных структур. Встаёт задача понимания этих сложных, нелинейных процессов в СЭС и управления ими. Для возможности сознательного воздействия на развитие СЭС их модели должны быть управляемыми и включать в себя процессы принятия решений, дающих возможности изменения политических, экономических, экологических и других структур. Оптимально управление динамическими СЭС с помощью имитационных моделей должно показывать переходные процессы, приводящие к эволюционному движению без катастроф к новым желаемым структурам [1; 7; 8].
Материалы и методы исследования
Пусть состояния СЭС характеризуется n-мерным вектором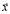 
, компоненты которого являются основными, существенными переменными, характеризующими состояние системы, и k-мерным вектором управляющих параметров 
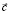, компоненты которого влияют на поведение 
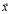. Введём скорость изменения состояния 
,
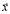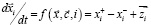, (1)
где i = 1, 2, N, и N – число регионов в СЭС, балансовые векторы xi+ и xi– учитывают члены увеличения и замедления скорости изменения вектора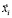 
, то есть 
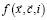и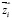 
– учёт влияния границ на i-участке СЭС. При малых отличиях в соседнем участке он может быть заменён на производную 
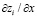, учитывающую степень влияния границ. Решение задачи Коши для нелинейных систем (1) с необходимостью должно иметь огромное количество начальных данных для: производственных, финансовых, социальных, экологических и т.д. параметров. Даже для малых прогнозных интервалов это приводит к трудно проверяемым результатам [4-6]. Встают вопросы их решения, моделирования процессов и управления ими. Задача управления динамическими моделями СЭС имеет смысл при плавном эволюционном развитии, когда параметры системы можно считать квазистатическими. Примеры исследования таких задач рассматривались нами ранее для рынков конкурирующих производств, финансовых структур, рынков трудовых ресурсов [1-3], а для рынков производства с учётом экологических проблем исследованы в работах [5; 8]. Такие условия реализуются вблизи квазиравновесных состояний систем, которые определяются соотношением в точке с нулевой скоростью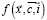 
f(x(c), c, i) = 0. (2)
При управляющем параметре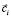 
однозначное разрешение уравнения стационарности (2) даёт кривую равновесных состояний систем 
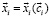. Однако при нарушении условий разрешимости уравнения стационарности в точке 
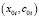возможно появление новых стационарных ветвей решения в фазовом пространстве, т.е. происходит катастрофа бифуркации кривых равновесия [1; 4; 5]. Скорость изменения параметров систем определяется функцией 
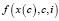, значение которой можно искать в градиентном приближении, введя синергетический потенциал для СЭС в виде 
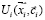уравнением (3) [1]. Выразим скорость изменения вектора параметров СЭС через синергетический потенциал СЭС с помощью уравнения
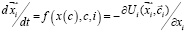. (3)
На структурно неустойчивой фазовой траектории возможно появление в области новых критических точек катастроф трудностей с управлением СЭС [5-7]. Как показывает численное моделирование решения уравнения (3), возникающие хаотические бифуркации на неустойчивой ветви перемежаются периодами гладкого эволюционного развития систем [1; 4; 5]. Система уравнений (1)–(3) является основной в дальнейшем исследовании имитационных моделей.
Модели систем и функции управления
Локальные функции управления могут быть использованы для следующих целей: достижение экономической оптимизации в регионах на краткосрочную перспективу; достижение политических и экономических целей. При моделировании СЭС важным является определение цели её функционирования и возможность выбора показателя эффективности при различных вариантах принятия решения. Задача управления заключается в определении оптимальной стратегии развития СЭС. Оптимальная стратегия вполне описывается целевыми функциями и их оптимумами. Метод динамического программирования при решении уравнений развития СЭС обеспечивает оптимальность решения, что следует из принципа оптимальности Беллмана [4].
Модель динамической СЭС, определяемая уравнениями (1) – (3), является многопараметрической. Существенные для описания представленной модели параметры, определяющие целевую функцию, неоднородны. Для реальных СЭС количество существенных переменных различного типа и сложности достигает несколько десятков или сотен. Работать с моделями столь большой параметрической размерности практически невозможно. Поэтому одной из сложных и необходимых задач представляется выбор минимального количества «грубых» функций или «параметров порядка», которые не реагируют на мелкие флуктуации и потому приемлемы для функций описания динамических СЭС и управления ими в квазистатическом режиме. Логично принять грубыми элементами используемые основные макроэкономические, социальные и экологические категории. Отбор параметров модели можно проводить методом экспертной оценки [7; 8]. Для экономических моделей в качестве основы можно использовать такие параметры, как общий объем валового продукта, параметры производственных, финансовых и трудовых ресурсов. Для социальных, экологических подсистем это другой набор параметров порядка, использованных нами ранее [1-3].
Проблемы устойчивости решений
Можно выделить два аспекта в исследованиях динамических моделей СЭС: проблемы устойчивости и проблемы качества решения нелинейной системы уравнений (1) – (3). Получение решений систем дифференциальных уравнений на длительные отрезки времени исходя из начальных данных – это задачи Коши для системы нелинейных дифференциальных уравнений. В математике нет общей теории решения систем нелинейных дифференциальных уравнений. Поэтому иногда предлагается проведение исследования решений модели СЭС с помощью дискретных аналогов – разностных алгебраических уравнений для дискретных приращений при машинном счёте [1; 4; 5]. При расчётах задачи Коши на длительные времена в реальных моделях СЭС (1) – (3) число уравнений для параметров порядка велико и возникает проблема недостаточности исходной информации в базах данных, используемых в процессе моделирования. При этом ошибки или неточности в начальных данных в расчётах параметров будут расти экспоненциально, что означает сильную зависимость точности решений задачи Коши от наличия точной базы исходных данных.
Другая проблема возникает из-за сложности самой модели, представляющей собой систему большого числа связанных математических соотношений. Расчёты по взаимосвязанным системам уравнений требуют применения методов численной математики, причём в итерационных схемах может иметь место заметное накопление вычислительной погрешности.
Особые благоприятные условия для управления динамическими моделями СЭС возникают при плавном эволюционном развитии систем, когда параметры системы можно считать квазистатическими при выполнении условия (2). Решение уравнения (2) в стационарной точке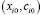 
даёт возможность появления новых кривых состояний системы 
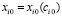, которые квазиравновесны, т.е. происходит бифуркация кривых равновесия [1; 4]. Поэтому в теории моделирования СЭС нужно иметь в виду возможную смену моделей функционирования и смену структур систем, что приводит к трудностям управления системами. В связи с этим необходимо: во-первых, проведение бифуркационного анализа фазовой траектории, то есть выявление критических точек на траектории; во-вторых, выявление наличия неустойчивости ветвей при прохождении неустойчивых критических точек.
Рассмотрим поведение СЭС вблизи стационарной критической точки, введя отклонение параметра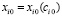 
от стационарного значения. Учёт членов разложения синергетического потенциала возрастающего порядка проведён нами ранее и приводит к последовательности «моделей катастроф» [1; 4]. При учёте в синергетическом потенциале уравнения (1) 
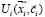нелинейных многочленов параметра до степени 2, модель описывают катастрофу «складка». Она возникают в производственных моделях управления ресурсами и моделях экологии [2; 6]. Катастрофы, описывающие социальные эксцессы в обществе, возникают, когда уравнения содержат нелинейности до четвёртой степени параметра порядка. Эта модель носит название «катастрофа сборка» и рассмотрена для конкретных моделей СЭС в работах [1; 3; 5]. При этом подходе нелинейные члены разложения входят с различными коэффициентами и знаками в потенциал уравнения (1) и входят в балансовые векторы 
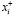и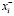 
уравнения соответственно.
Результаты исследования и их обсуждение
Простые математические закономерности иногда неэффективны. Модель роста населения Земли по Мальтусу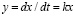 
приводит к очень быстрому экспоненциальному росту населения. В работе [6] показано, что такая «жёсткая» модель, не учитывающая ограниченность пищевых ресурсов, должна быть заменена «мягкой» моделью, в которой должна быть учтена обратная связь через зависимость коэффициентов от результата расчёта, 
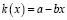, что приводит к логистической модели 
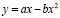. Или в безразмерном виде
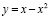. (4)
На рис. 1 представлен график функции k(x)x, положительной между точками 0 и 1. В каждой точке под кривой существует векторное поле точек скоростей параметра x, с направлением к точке 1. Таким образом, «мягкая» модель Мальтуса предсказывает установление режима с населением, стремящимся к фокусу 1. Мягкая логистическая модель широко используется при описании популяции живых систем с конкуренцией и борьбой за кормовую базу. В обществе можем наблюдать конкуренцию организаций: фирм, предприятий, банков, предпринимателей, использующих передовые технологии для устранения конкурентов. Ведение «мягких» моделей при имитационном планировании стабилизирует систему, которая без обратной связи разрушается при оптимизации параметров [1; 6; 8].
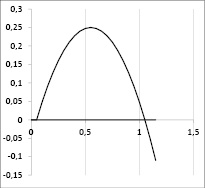
Рис. 1. График логистической кривой
Рассмотрим с помощью логистической модели сегментированный рынок труда. Полагая этот рынок меняющимся медленнее, чем остальные рынки, и учитывая его сегментированность, введём концентрацию работников xi, занятых в i-том сегменте. Учитывая в системе уравнений (1) – (3) члены разложения не выше квадратичных
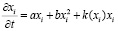, (5)
где a – коэффициент самовоспроизводства, b – учёт конкуренции, k – учёт влияния социальных, психологических, технологических и других факторов на рынок.
На рис. 2 видна заштрихованная область между двумя линиями, в которой возможны квазиравновесные изменения состояния системы. Стрелки внутри графика указывают, что система стремится при любых x0 со временем к устойчивому состоянию, определяемому комбинацией экономических и социальных факторов. Сама устойчивая точка является пересечением параболы нелинейного ограничения скорости роста y логистической кривой за счёт конкуренции на рынке и прямой kx – описывающей влияние социальных, технологических и культурных факторов.
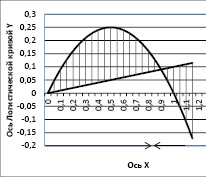
Рис. 2. Область существования решений уравнения (5)
Таким образом, появляется возможность за счёт изменения этих факторов менять область существования квазиравновесных состояний в логистической модели. К социальным и культурным факторам относятся уровень грамотности трудовых ресурсов, гендерные отношения, уровень женской эмансипации. При больших коэффициентах k, определяющих тангенс наклона этой линии, есть ситуация, когда станет невозможным пересечение линий и, следовательно, возможна потеря устойчивости сектора трудовых ресурсов. К культурным факторам, определяющим возможность управления моделью, относятся изменение гендерных отношений, уровень женской активности и т.д. Таким образом, введение обратной связи в модели (5) позволяет управлять и получать разумные результаты. Этот подход позволяет получать разумные результаты и при использовании более сложных нелинейных моделей в изучении СЭС. Доказательство, что при степенях параметров в потенциалах r ≤ 4 семейство сингулярностей устойчиво и эквивалентно одному из семейств катастроф в теории Тома [1]. Основные приложения теории катастроф представляют собой катастрофы типа «сборка» и «складка» [1; 4]. Рассмотренная выше задача управления трудовыми ресурсами относится к катастрофам типа «складка». При таком подходе нелинейные многочлены разложения потенциала чётные и нечётные в уравнении (1) естественно входят в балансовые векторы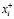 
и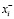 
. Для более сложных моделей СЭС с нелинейностями в потенциале до пятой степени по параметру порядка приходим к катастрофе типа «ласточкин хвост».
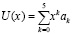, (6)
Исследование проблемы устойчивости и неустойчивости моделей СЭС при заданном синергетическом потенциале (6) с помощью дифференциального уравнения (3) может быть проведено с помощью теоремы Ляпунова и сведено к исследованию функции скорости изменения параметров системы f(x(c), c, i). На рис. 3 представлен график расчёта фазовой диаграммы «мягкой» модели катастрофы «ласточкин хвост». Видно наличие двух заштрихованных разделённых областей устойчивости модели. Синергетический потенциал U в уравнении (3) является функцией Ляпунова системы. Минимум или максимум в любой стационарной точке с фазовой траектории будет определятся минимумом или максимумом синергетического потенциала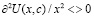 
. На рис. 3 точки А отталкивают фазовые траектории, а точки В притягивают их. На рис. 4 видны две волны потенциала, появляющиеся в результате наличия в потенциале многочленов чётных и нечётных степеней параметра порядка. При наличии в модели учёта более высоких степеней параметра порядка будут появляться следующие горбы потенциала, говорящие о цикличном поведении фазовых траекторий, как указывалось ранее [9].
Для имитационной модели оптимальным будет решение, позволяющее без катастроф переходить во все квазиравновесные области. Это достигается управлением наклона линии прямой, угол наклона которой регулируется параметрами модели. На рис. 4 показана возможность эффективного управления наклоном линии для доступа равновесных фазовых траекторий в любую область доступных фазовых состояний – заштрихованные области. Вне этих областей траектории испытывают распады и возвращаются в область устойчивости.
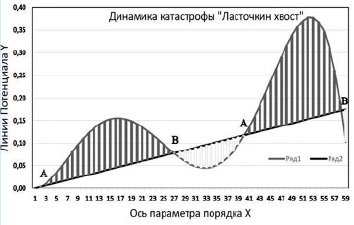
Рис. 3. График устойчивости потенциала (6)
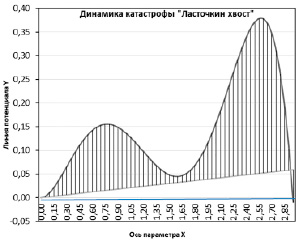
Рис. 4. График возможностей перехода квазиравновесно из одного горба графика в другой
Заключение
Синергетика уже занялась процессом моделирования динамки СЭС. Между тем даже в развитых экономиках наблюдаются процессы цикличности экономики и социальных проблем общества. Страны сталкиваются с такими процессами, как обязательная цикличность зарождения более адекватного сообществу социального и экономического порядка в виде технологических революций, социальных проблем, которые зарождаются сначала как идеи в виде флуктуаций. Хаос фактически даёт разрушение старых структур и порождает новую упорядоченность в структуре и экономике общества. Циклы экономического развития известны давно. Как показано в нашей работе, процесс развития СЭС естественно сопровождается автоколебаниями областей состояния систем. Поэтому проблема прогноза и управления в моделях становится трудной, связанной с построением систем искусственного интеллекта и актуальной.