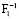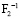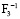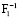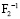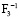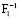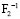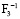Анализ риска и управление им уже давно являются научным инструментом, который применяется практически везде, где существует потенциальная опасность [1–3]. Многие исследователи пытаются решить задачи риск-анализа, используя нелинейную динамику, теорию катастроф и другие методы и подходы [1–3]. В первую очередь всегда интересует количественная оценка вероятности риска опасной ситуации и ожидаемого ущерба от нее [3–5]. Особое место здесь занимают математические задачи, которые являются некорректными. Впервые понятие «корректно поставленная задача» было введено Ж. Адамаром в 1923 году [6, 7]. Раньше представлялось, что такие задачи не имеют никакого практического смысла, однако академик А.Н. Тихонов предложил подход к решению таких задач, который получил название методов регуляризации [1, 6, 7]. Они заключаются в том, что необходимо учесть дополнительную информацию о решении некорректной задачи и переформулировать ее так, чтобы она стала корректной.
Рассмотрим опасные объекты металлургического предприятия, к которым относятся краны, эксплуатирующиеся на всех видах производств, но особенно они представляют опасность на основных производствах: разливке стали, кислородно-конвертерном производстве и др.
Для успешного решения задачи анализа риска необходимо сформулировать прямую и обратную задачи, учесть дополнительную априорную информацию, представить модельный пример ее решения, на основе решения выдать рекомендации для технологических решений.
Материалы и методы исследования
В задачах анализа и управления рисками можно выделить следующие некорректные задачи:
1) задача прогноза, в которой можно прогнозировать будущее состояние системы, исходя из ее настоящего. В данном случае приходится иметь дело с очень большим объемом информации, который не всегда возможно учесть;
2) задачи риск-анализа сложных технических систем, сооружений, которые должны эксплуатироваться в течение длительного времени без аварий и катастроф, потому что они представляют очень большую опасность. В этом случае безопасность элемента, объекта, системы будет определяться большим множеством малых факторов;
3) задачи мониторинга фактического технического состояния опасных объектов и принятия решения в очень короткие сроки. Такие задачи требуют разработки новых подходов.
Сформулируем прямую задачу. Есть модель риска совокупности опасных объектов, которая порождает их безаварийное и аварийное состояние (в частности, авторами рассматривались опасные объекты основных производств металлургического предприятия) [2, 3]. Рассмотрим операторное уравнение:
Fm = y, m ∈ M, y ∈ Y, (1)
где F – оператор преобразует элемент пространства M(m) рассматриваемых объектов и их состояний в пространство риска опасных объектов Y(y).
Решение уравнения (1) является по своей сути неустойчивым по отношению к ошибкам исходных данных оператора F и правой части y, то есть такая задача является некорректной [6, 7]. В самом деле, если мы будем рассматривать большое количество опасных производств металлургического предприятия, то очень сложно вычленить здесь опасные и неопасные объекты, а также можно потерять определенную информацию, налицо будут ошибки в исходных данных.
Введем строгое определение корректно поставленной задачи по Ж. Адамару [6, 7]:
1) уравнение (1) разрешимо для всех y ∈ Y;
2) решение единственно;
3) решение устойчиво по возмущению правой части.
Под некорректной задачей понимается такая, для которой не выполняется хотя бы одно из перечисленных условий [6, 7].
Обратная задача состоит в вычленении относительно малых факторов или параметров, элементов, которые влияют на потенциальную опасность таких объектов, с помощью которых могут быть созданы системы мониторинга на сложных технических сооружениях и объектах с целью поддержания такой совокупности объектов в нормальном эксплуатационном состоянии. Тогда:
F–1Fm = F–1y, m ∈ M, y ∈ Y, (2)
m = F–1y, m ∈ M, y ∈ Y, (3)
Неоднозначность решения такой задачи приводит к необходимости определять не искомую модель, а ее приближенные осредненные характеристики. Кроме этого, часто при решении прикладных задач мало информации, наблюдения за объектами ограничены.
Выходом из положения при решении такой задачи может служить применение метода регуляризации Тихонова, когда вводится априорная информация с целью перевода некорректной задачи в корректную, для которой могли быть разработаны эффективные вычислительные алгоритмы.
Результаты исследования и их обсуждение
Проиллюстрируем такой подход на следующем примере. По данным [1–3] введем априорную информацию на совокупности опасных объектов – металлургических кранах. Рассмотрим конструкцию металлургического крана. Его функция заключается в поднимании, перемещении и опускании грузов. Выделим три основные группы элементов такого объекта:
– металлоконструкция моста: пролетные и концевые балки главного и вспомогательного мостов; зоны приварки кронштейнов проходных галерей моста к стенкам балок; нижние пояса балок;
– пролетные балки вспомогательного моста;
– траверса механизма главного подъема: крюки; металлоконструкция траверсы; храповая передача механизма главного подъема: храповое колесо; собачки; оси крепления собачек; прижимные пружины; осевое крепление храпового колеса.
Концептуальная модель риска и вероятностная модель его нагруженности описана в [2, 3].
Концептуальную модель функции качества будем рассматривать в следующем виде:
K(t) = f(Б(t), Н(t), Э(t)), (4)
где К(t) – функция качества технической системы (объекта, элемента); Б(t) – функция безопасности; Н(t) – функция надежности; Э(t) – функция экономической эффективности.
Тогда обобщающее условие анализа и оценки качества на основе риск-анализа можно записать как:
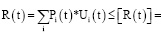
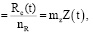(5)
где R(t) – риск – сочетание вероятностей Pi(t) возникновения аварий и катастроф и ущербов Ui(t) от них; nR – запас по рискам (nR ≥ 1); Rc(t) – критический риск; затраты Z(t), связанные с формирующимися рисками R(t); mZ – коэффициент эффективности затрат (mZ ≥ 1); i – рассматриваемые элементы.
Очевидно, что функцию качества технической системы (элемента, объекта) можем представить в следующем виде:
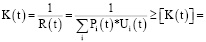
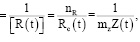(6)
где [K(t)] – допускаемый уровень качества. Таким образом, качество будет определяться риском аварии опасного объекта и ожидаемого ущерба от нее.
Предположим, что несущая способность конструкции металлургического крана (опасного объекта) будет оператор F–1 в (2) и (3):
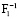– несущая способность конструкции нормальная (надежность всех элементов больше или равна 0,841);
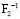– несущая способность конструкции предельно допустимая (надежность всех элементов больше или равна 0,479);
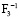– несущая способность конструкции катастрофическая (надежность всех элементов меньше или равна 0,250).
Тогда можно записать, что несущая способность конструкции металлургического крана (опасного объекта) подчинена:
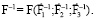(7)
Используя априорные данные численных и расчетных данных количества циклов, напряжений и деформаций, а также предложенный метод исследования, представим динамику несущей способности конструкции металлургического крана, состоящего из трех основных групп элементов [3–5].
Матрицу оператора F–1 несущей способности конструкции представим в виде таблиц 1–3:
Таблица 1
Несущая способность в начале эксплуатации
|
|
|
|
|
0,8410 |
0,1090 |
0,0500 |
|
0,3710 |
0,4790 |
0,1500 |
|
0,2500 |
0,5000 |
0,2500 |
Таблица 2
Несущая способность через 15 лет эксплуатации
|
|
|
|
|
0,4257 |
0,4855 |
0,0889 |
|
0,4568 |
0,3539 |
0,1894 |
|
0,4425 |
0,3200 |
0,2375 |
Таблица 3
Несущая способность через 25 лет эксплуатации
|
|
|
|
|
0,3157 |
0,2959 |
0,3883 |
|
0,3154 |
0,2935 |
0,3911 |
|
0,3156 |
0,2946 |
0,3898 |
Зададим вектор-столбец риска опасного объекта по материалам [2, 3]:
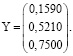
Применив методы линейной алгебры, получим вектор-столбцы для рассматриваемых групп элементов конструкции металлургического крана (объекта):
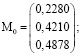
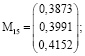
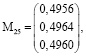
где М0, М15, М25 – вероятности элементов опасного объекта, на которые следует обратить внимание в начале эксплуатации, через 15 и 25 лет соответственно. Так, видим, что необходимо в начале эксплуатации и через 15 лет обратить внимание на элементы третьей группы, через 25 лет – на элементы второй группы. Следовательно, особое внимание нужно уделять траверсе механизма главного подъема, крюкам, металлоконструкции траверсы, храповой передаче механизма главного подъема, храповому колесу и собачкам, оси крепления собачек, прижимным пружинам, осевому креплению храпового колеса, металлоконструкции балок моста. Полученные данные хорошо согласуются со статистическими [1–3], что говорит о правильности такого подхода.
Заключение
Количественная оценка анализа риска опасного объекта в процессе эксплуатации сводится либо к экстраполяции его настоящего технического состояния в прогнозе в будущем, либо к оценке текущей ситуации, либо к оценке относительно незаметных, малых параметров или элементов, которые в процессе длительной эксплуатации могут оказать очень существенное влияние на его безопасность. Даже небольшое возмущение с их стороны может привести к катастрофическим проблемам. Все такие задачи являются некорректными.
Предложенный подход к применению метода регуляризации для оценки анализа параметров опасных объектов, которые могут повлиять на его безопасность с учетом дополнительной априорной информации, расширяет возможности метода регуляризации А.Н. Тихонова и создает большое потенциальное поле для исследований. Математических примеров решений некорректных задач много, а качественных, модельных, имеющих реальное применение, как, например, анализ риска опасного объекта или сооружения, на сегодняшний день недостаточно. Для приведенной задачи вычислительный алгоритм становится достаточно эффективным, значительно упрощается, хотя при этом необходимо учитывать величину ошибки.
Основные проблемы, которые здесь возникают, – выбор пространства групп элементов, которые являются определяющими для опасного объекта в процессе эксплуатации, и выбор пространства вероятностей риска.
Таким образом, создание решения большого класса некорректных задач в анализе риска опасных объектов металлургического предприятия обратных задач и их решение позволят оценивать и осуществлять мониторинг основных групп элементов конструкций опасных объектов, принимать правильные научно-технологические и управленческие решения с целью снижения их аварийности.
Модели принятия решений оценки качества оборудования будут включать стратегию управления риском и оценку экономической эффективности от эксплуатации объекта металлургического предприятия как составляющих его качеств.
По [1–3] могут быть предложены следующие модели принятия решений: модель гарантированной надежности, модель штатных аварий, модель идеального мониторинга.
Модель гарантированной надежности – это тот случай, когда опасный объект (металлургический кран), отработавший гарантийный срок эксплуатации, более не эксплуатируется. Достоинством такой модели является то, что не нужен мониторинг. Недостаток заключается в том, что время до аварии может быть маленьким, собственник может отказаться от эксплуатации, хотя на самом деле объект может находиться в работоспособном состоянии.
В модели штатных аварий при проектировании опасных объектов обязательно учитываются так называемые штатные, или нормальные, аварии.
В этом случае, если хорошо отработана система технического обслуживания (вероятность р > ½), аварии можно избежать. Управление риском в этом случае сводится к выбору режима технического обслуживания и проектного срока эксплуатации.
В модели идеального мониторинга в критической ситуации нужно будет просто прекратить эксплуатацию крана. Такая высокоэффективная система мониторинга предполагает достаточно серьезные затраты.
Совместное решение некорректной задачи анализа риска опасных объектов металлургического предприятия и предложенные модели могут существенно повысить эффективность их эксплуатации.
При использовании предложенного подхода представляется возможным построение вероятностных моделей для опасных объектов, группы объектов, сложной системы объектов (металлургическое предприятие), связывающих их свойства и вероятность их отказа, ведущего к аварии. Свойства таких систем изменяются с течением времени. Диагностика и мониторинг фиксируют эти изменения.