Искусственные нейронные сети (РБФ-сети), основанные на радиально-базисных (то есть радиально-симметричных) функциях, представляют собой класс нейронных сетей прямого распространения, впервые предложенный в 1988 г. в [1]. РБФ-сети изначально предназначались для интерполяции и аппроксимации одномерных и многомерных данных [2], но их также можно использовать для решения задач кластеризации [3] и классификации данных [4].
Искусственные нейронные сети на основе радиально-базисных (иначе – радиально-симметричных) функций (РБФ-сети) – один из классов нейронных сетей прямого распространения, впервые предложенный в 1988 г. в работе [1]. Изначально предназначенные для интерполирования и аппроксимации одномерных и многомерных данных [2], РБФ-сети могут также использоваться при решении задач кластеризации [3] и классификации данных [4]. Однако основная цель данной работы – исследовать интерполирующую способность РБФ-сетей в одномерных и многомерных задачах при выборе различных видов активационной радиально-базисной функции. Для достижения поставленной цели решаются следующие задачи:
– выбор вида радиально-базисных функций для сравнения;
– разработка специализированного программно-алгоритмического обеспечения для расчетов;
– сравнительный анализ интерполирующей способности РБФ-сетей для одномерных и многомерных задач;
– сравнительный анализ интерполирующей способности РБФ-сетей для различных видов активационной функции.
Общая структура и алгоритм обучения РБФ-сети
Структура РБФ-сети содержит два слоя нейронов. Выходы первого слоя активируются множеством радиально-базисных функций, как правило, функциями Гаусса (функция 1):
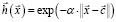, (1)
где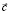 
– вектор центров (координат вертикальных осей симметрии функции) множества радиально-симметричных функций; 
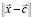– евклидова норма вектора отклонений входной переменной от центров радиально-симметричных функций; α – параметр насыщения.
Альтернативы функции Гаусса (рис. 1) предложены в работе [5]. К ним относятся:
– функция Лапласа (функция 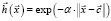2):
; (2)
– функция Коши (функция 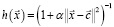3):
; (3)
– кусочно-линейная функция (функция 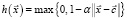4):
; (4)
– кусочно-нелинейная функция Вигнера (функция 5):
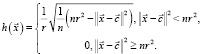
(5)
В последнем соотношении используются следующие дополнительные обозначения: n – размерность задачи; r – предельный разрешенный радиус отклонения входных переменных от центров радиальных элементов.
Следует отметить, что перечисленные функции по-разному ведут себя в части области определения, задействованной в вычислениях нейронной сети.
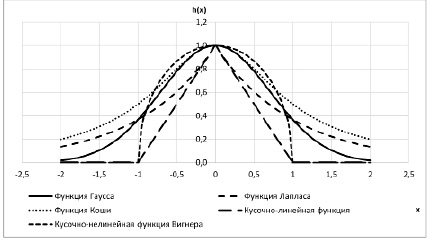
Рис. 1. Варианты функций для использования в РБФ-сетях
Одна из наиболее существенных особенностей – негладкость ряда функций (Вигнера, Лапласа и кусочно-линейной зависимости) в отдельных точках, что затрудняет оптимизацию параметров их настройки. Тем не менее принципиально разная поверхность отклика делает эти функции интересными для исследования возможности их применения в РБФ-сетях.
Состав и количество входов и выходов определяются решаемой задачей [3]. Входы соответствуют аргументам интерполирующей зависимости. Выходы соответствуют ее отклику. Первый из двух слоев (скрытый слой) содержит радиальные элементы, служащие для оценки степени отклонения входов от узловых векторов. Количество нейронов скрытого слоя может варьироваться от одного до числа, не превышающего количество обучающих примеров. Выходы нейронной сети представляют собой линейные комбинации выходов нейронов скрытого слоя [6].
В начале обучения РБФ-сети задаются центры радиально-базисных функций и параметр насыщения. Теоретически значения параметра насыщения могут быть разными для нейронов скрытого слоя. Далее методами линейной алгебры рассчитываются весовые коэффициенты линейного выходного слоя:
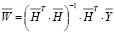, (6)
где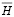 
– характеристическая матрица значений радиально-базисных функций, количество строк которой равно количеству обучающих примеров, а количество столбцов – количеству скрытых нейронов; 
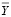– матрица выходов с количеством строк, равным числу обучающих примеров, и количеством столбцов, равным числу выходов нейронной сети.
Постановка задачи интерполирования, исходные данные
При решении одномерной задачи интерполирования РБФ-сеть будет иметь один вход и один соответствующий ему выход (рис. 2). Для интерполирования данных используем, например, 5 узловых точек, которые будут соответствовать центрам радиальных элементов скрытого слоя.
При многомерном интерполировании количество входов сети должно соответствовать размерности задачи. Как и в первом случае, сеть будет иметь единственный выход (рис. 3). Для двумерной задачи интерполирующая способность, эквивалентная одномерному варианту с пятью узлами, ожидается в случае уже 25 скрытых нейронов (количество всех возможных сочетаний узлов интерполяции). Для трехмерной задачи – в случае 125 скрытых нейронов. Соответствующим образом размерность задачи влияет и на требуемый объем обучающей выборки.
Проблема степенного роста объема вычислений для задач интерполирования высокой размерности с помощью РБФ-сетей решается в работе [7]. Здесь слой многомерных радиально-базисных функций заменяется двумя скрытыми неполносвязными слоями: первый – одномерные радиальные элементы, второй – вычислительный слой, группирующий и обрабатывающий определенным образом выходы первого.
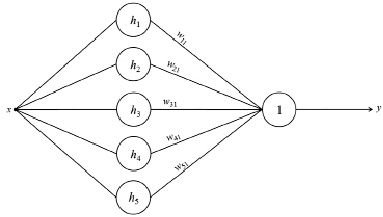
Рис. 2. Структура РБФ-сети для интерполирования одномерной зависимости
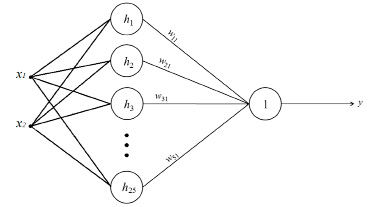
Рис. 3. Структура РБФ-сети для интерполирования двумерной зависимости с пятью узлами интерполяции
В результате такой замены объем вычислений сокращается, а вычислительная ошибка (как средняя, так и максимальная по выборке) в большинстве случаев уменьшается.
На основе набора доступных экспериментальных данных необходимо определить наиболее точную настройку для РБФ-сети и рассчитать веса нейронов выходного слоя, чтобы найти одну и ту же многомерную зависимость y = y(x→) на обучающей выборке для любой возможной комбинации значений независимых переменных, которые охватывают диапазон изменения переменных в обучающей выборке.
Разработка программно-алгоритмического обеспечения для расчетов
Специализированное программно-алгоритмическое обеспечение для интерполирования зависимостей нейронной РБФ-сетью было разработано на языке программирования C++11 [8, 9] с использованием мультиплатформенного фреймворка Qt 5.8 [10]. Программа содержит системные вкладки, отвечающие за настройку нейронной сети, выбор обучающих примеров и интерфейс вывода результатов работы. Формат предоставления результатов моделирования достаточно гибкий, что позволяет максимально удобно использовать ее функциональные возможности для проведения поставленной исследовательской задачи.
Для корректной работы программного комплекса необходимо устройство под управлением операционной системы Windows, 60 МБ ОЗУ и примерно 80 МБ памяти на жестком диске, а также наличие встроенной видеокарты [11]. При работе программы производится автосохранение результатов работы программы, а также всех параметров настройки нейронной сети и обучающей выборки. При запуске программный комплекс в случае обнаружения автосохранения подгружает прошлое состояние сети. Все данные пользователь может сохранять в ручном режиме для последующего использования. На рис. 4 показана форма конфигурации РБФ-сети. Вкладку можно использовать, чтобы установить структуру (количество скрытых нейронов), также установить параметры насыщения, выбрать центры радиальных элементов и вычислить весовые коэффициенты выходного слоя. Центры радиальных элементов могут задаваться автоматически с учетом количества экспериментальных точек и плотности их распределения по оси независимой переменной.
На рис. 5 показан графический вывод результатов интерполяции одномерной функции. Пользователь может настроить формат визуализации графика, масштабировать его, распечатать, сохранить в файл.
Исследование влияния выбора радиально-базисной функции на ошибку интерполирования
Разработанное программно-алгоритмическое обеспечение использовано для исследования и анализа интерполирующей способности нейронных сетей с различными радиально-базисными функциями в одномерных и многомерных задачах [12].
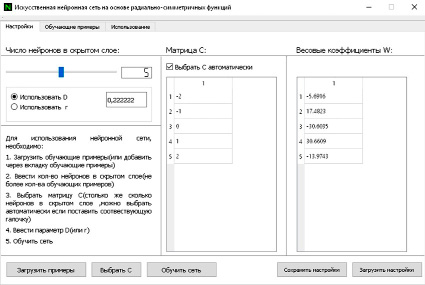
Рис. 4. Форма настройки РБФ-сети
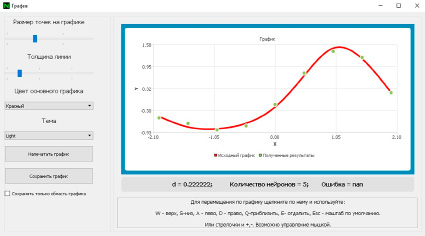
Рис. 5. Форма графического вывода результата интерполирования одномерной функции
Рассматривались одномерная РБФ-сеть с 5 скрытыми нейронами и двумерная РБФ-сеть с 25 скрытыми нейронами. Для генерации обучающих и тестовых данных использованы следующие нелинейные зависимости:
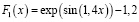; (7)
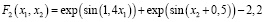. (8)
Результаты средних относительных ошибок сетей с разными радиально-базисными функциями
|
Функция Гаусса |
Функция Лапласа |
Функция Коши |
Кусочно-линейная функция |
Функция Вигнера |
|
|
F1(x) |
2,5 |
3,7 |
2,3 |
3,4 |
2,3 |
|
F2(x1, x2) |
2,3 |
3,3 |
2,8 |
1,9 |
4,9 |
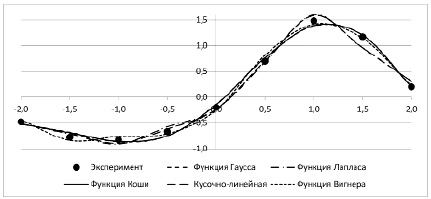
Рис. 6. Описание исходных данных нейронными сетями с различными РБФ
Для исследования интерполяционной способности одномерной сети RBF 5 узлов из экспериментального набора были выбраны в качестве центров радиальной базисной функции из выборки, состоящей из 16 примеров. Эта структура нейронной сети содержит 1 вход, 5 скрытых радиальных элементов и 1 выход.
Используя точки с теми же комбинациями координат, решалась задача интерполяции данных с помощью двумерных нелинейных функций. Из 50 обучающих векторов 25 были выбраны в качестве центров радиально-базисных функций.
В зависимости от выбранной функции в таблице показана средняя относительная ошибка, полученная с использованием одномерных и двумерных нелинейных функций, которые рассчитываются на основе нормализованных данных.
Для интерполирования рассмотренной одномерной зависимости наиболее подходящими функциями активации оказались функции Вигнера, Гаусса и Коши. Кусочно-линейная зависимость и функция Лапласа дали заметно большую среднюю относительную ошибку. Для интерполирования двумерной функции наилучшим образом проявили себя кусочно-линейная, Гаусса и Коши. При использовании функций Вигнера и Лапласа получены более высокие значения ошибки. Отметим, что в целом погрешности одномерной и двумерной задач оказались сравнимыми. Полученные результаты позволяют рекомендовать к использованию в РБФ-сетях функции Гаусса и Коши. Проблемы с эффективным использованием функций Лапласа, Вигнера и кусочно-линейной зависимости вызваны в первую очередь их недифференцируемостью в отдельных точках области определения.
На рис. 6 представлены графические результаты математического описания экспериментальных данных нейронной сетью с различными радиальными базисными функциями.
Исследование влияния структуры и настроек РБФ на ошибку интерполирования
В рамках нашего исследования влияния структуры нейронной сети и значений параметра насыщения радиальной базисной функции на ошибку гауссовой аппроксимации были получены следующие результаты.
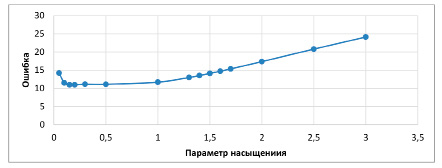
Рис. 7. Оптимизация параметра насыщения одномерной задачи
Рис. 8. Оптимизация параметра насыщения двумерной задачи
1. Максимально возможное значение, ограниченное числом экспериментальных точек, как правило, значительно снижает погрешность аппроксимации.
2. Кроме того, выбор оптимального параметра насыщения позволяет уменьшить ошибку аппроксимации в 1,5–2,0 раза. Это относится к той же сетевой структуре RBF.
3. В рассматриваемом примере оптимумы расположены в пределах [0,15; 1] при использовании одномерной функции (рис. 7) и двумерной функции [0,25; 1] (рис. 8), однако в общем случае значение параметра насыщения зависит от диапазона изменения независимой переменной, известного числа экспериментальных точек и среднего значения расстояния между соседними точками.
Заключение
По результатам исследования различных функций активаций можно рекомендовать к использованию в РБФ-сетях функции Гаусса и Коши. В то же время следует учитывать, что при решении задач интерполирования зависимостей не всегда данные функции могут давать корректное описание экспериментальных данных. В этой связи в ходе нейросетевого моделирования кроме выборов параметров насыщения и центров радиальных элементов рекомендуется отдельно подбирать вид радиально-базисной функции. При этом крайне желательно, чтобы она была дифференцируема во всех точках, принадлежащих области определения.
Согласно полученным результатам РБФ-сети могут успешно использоваться для решения задач интерполирования как сложных многомерных, так и одномерных функций. Несмотря на то, что подбор параметров настройки таких нейронных сетей представляет собой отдельную, достаточно сложную и времяемкую задачу, эффективное ее решение способно значительно улучшить качество получаемого математического описания.