Многие сайты собирают рейтинговые оценки фильмов, книг, музыкальных произведений, товаров и многих других объектов. Каждая рейтинговая оценка принадлежит некоторой порядковой шкале, например {0, 1, 2, 3, 4, 5}. Обобщение рейтинговых оценок часто представлено в виде усредненных значений. Усреднение является не вполне корректной процедурой, так как порядковые шкалы не являются метрическими. Кроме этого, оценки выполняются разными людьми, которые интерпретируют одну и ту же шкалу по-разному. Обработка таких оценок с учетом подобных различий представляется актуальной задачей.
Для обработки рейтинговых оценок применяют методы коллаборативной фильтрации [1]. Рейтинговая оценка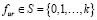 
выставляется субъектом u ∈ U (клиенты, пользователи, …) объекту r ∈ R (товары, фильмы, ресурсы,…). Матрица || fur || является сильно разреженной. Например, один зритель из нескольких тысяч оценивает десятки фильмов из большого их количества. Традиционное применение коллаборативной фильтрации заключается в прогнозировании не заполненных значений fur, определении степени сходства субъектов и объектов.
Рейтинговые оценки используются для ранжирования объектов. На эту процедуру существенно влияют индивидуальные склонности субъектов к переоценке или недооценке объектов. Возможны ситуации искажения результатов ранжирования в случае существенно неоднородных множеств оценщиков. Если большая часть оценщиков некоторого объекта склонны к завышению оценок, то и средняя оценка будет завышенной. Субъекты, выставляющие в основном высокие или в основном низкие оценки, будут значительно искажать результаты ранжирования. Таким образом, разные субъекты применяют разные шкалы, даже если они содержат одинаковое количество градаций. Для корректной статистической обработки таких данных необходимо установить соответствие разных шкал.
Материалы и методы исследования
Традиционно сопоставление шкал связывают с сопоставлением интервалов [2] интегральных характеристик, по которым определяются рейтинги. Кроме этого, соответствие шкал можно определять на основе статистических распределений оценок. Для данных, изучаемых в данной работе, такой подход оправдан статистической однородностью рассматриваемых наблюдений. Для его реализации нужно строить распределения оценок, зависящие как от параметров субъекта, так и от параметров объекта. Подобные распределения применяет Item Response Theory [3] для описания итогов тестирования с учетом латентных параметров, характеризующих трудности тестовых заданий и подготовленность тестируемых.
Среди методов коллаборативной фильтрации отмечается привлекательность моделей [4, 5], которые используют латентные параметры, характеризующие каждого субъекта и каждый объект. В результате существенно снижаются количество оцениваемых параметров и сложность алгоритмов, а также повышается точность моделирования. Подобный подход применяется [4] для решения традиционных задач коллаборативной фильтрации. Отмечается [5] близость моделей Item Response Theory, применяемых для обработки данных тестирования, и латентных моделей коллаборативной фильтрации.
В данной работе предлагается инструмент построения рейтинга объектов, который учитывает индивидуальные особенности применения порядковой шкалы каждым субъектом на основе моделей с латентными параметрами.
Предлагается следующая модель, описывающая получение оценки в виде последовательности шагов. В случае «неудачи» на l-м шаге (l = 1,…,k) с вероятностью 1 – pi оценка принимается равной l – 1, в случае «успеха» с вероятностью pi испытание продолжается на следующем шаге. Предполагается независимость шагов. Успешно выполнив все шаги, субъект выставляет максимальный балл k. Случайная величина X – итоговая оценка – будет иметь следующее распределение вероятностей:
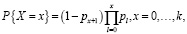
где для удобства полагается p0 = 1, pk+1 = 0.
Математическое ожидание X можно вычислить в виде следующей суммы:
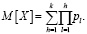
По аналогии с моделью «Partial Credit» [3], применяемой для анализа результатов тестирования, склонность субъекта u выставлять повышенные оценки будем измерять параметром θu, a l-й шаг оценивания объекта r будем характеризовать параметром δrl . Параметры определяют для субъекта u вероятности шагов оценивания объекта r:
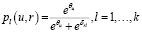
и вероятность оценки:
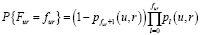
Очевидно, что, чем больше θu, тем сильнее распределение оценки Fur будет смещаться в сторону более высоких оценок. Параметры δr1.,…, δrk. определяют распределение оценки объекта r при некотором фиксированном θ и могут рассматриваться как характеристики объекта. Предполагается независимость всех шагов оценивания разными субъектами.
Для оценки параметров можно применить метод максимального правдоподобия – найти значения параметров, обеспечивающих максимум вероятности:
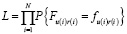
наблюдений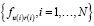 
, где u(i) – субъект i-й оценки, r(i) – объект i-й оценки, N – число наблюдений. Перейдем от функции максимального правдоподобия:
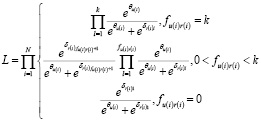
к ее логарифму:
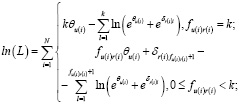
Условием достижения максимума будет равенство нулю частных производных:
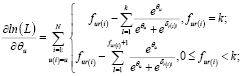(1)
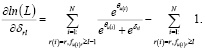(2)
Для решения таких уравнений в IRT предлагается использовать метод Ньютона. В этом методе в итерационной формуле:
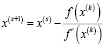
в числителе используется первая производная логарифма функции правдоподобия, а в знаменателе – вторая:
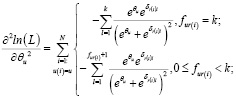
Отрицательные значения второй производной соответствуют вогнутости функции, что гарантирует сходимость предложенной процедуры поиска значений параметров.
Особенностью предложенной модели является то, что значение вероятностей не изменится, если все латентные параметры изменить на одну и ту же величину.
Для получения начальных значений положим в (1)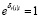 
. В этом случае параметр вычисляется как логарифм средней оценки субъекта u:
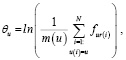
где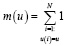 
– количество оценок
субъекта u.
Аналогично полагая в (2)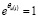 
, получаем:
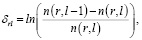
где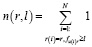 
– количество оценок
субъекта r,
не меньших l.
Если аргумент логарифма равен нулю, то начальное значение параметра приравнивается некоторому отрицательному значению, например δrl = –5, что соответствует почти единичной вероятности успеха на l-м шаге оценивания.
Для апробирования модели был выбран набор данных ml-latest-small с рейтинговыми оценками фильмов, который содержит 100 836 оценок для 9 308 фильмов от 610 зрителей. Данный набор данных размещен на сайте Social Computing Research at the University of Minnesota. Оценки включали половинки баллов от 0,5 до 5 и были переведены в целочисленную шкалу от 0 до 9. Для данного набора данных были определены латентные параметры субъектов (зрителей) и объектов (фильмов).
Для оценки адекватности модели предлагается применить дисперсионный анализ. Дисперсионный анализ позволяет оценить зависимость оценок от субъектов и объектов. Для оценки влияния субъектов сравниваются усредненные выборочные дисперсии по субъектам:
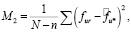
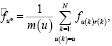
где n – количество субъектов,
с межгрупповой дисперсией:
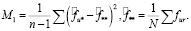
Статистики M1 и M2 являются разными оценками дисперсии одной и той же случайной величины в случае отсутствия влияния субъекта на оценку. Статистика F = M1 / M2, при условии одинакового нормального распределения и независимости вариаций среди оценок, будет иметь распределение Фишера со степенями свободы n – 1 и N – n. Как и следовало ожидать, проверка подтвердила предположение о наличии влияния субъектов на оценки. Аналогично была подтверждена зависимость оценок от объектов.
По такой же схеме были проверены гипотезы о независимости остатков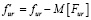 
от субъектов и объектов. Вычисления подтвердили эти гипотезы с доверительной вероятностью, близкой к единице.
Коэффициент детерминации:
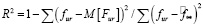
определяет «долю изменчивости», которую описывает модель. Для предложенной модели и массива оценок коэффициент детерминации составил 0,43. Не слишком большое значение коэффициента детерминации показывает, что оценки являются в большой степени случайными, а также в модели не учитывается множество других факторов, например характеристик фильмов и зрителей, оказывающих значимое влияние на формирование оценок. В целом предложенная модель позволяет получить более точные оценки по сравнению с простым усреднением.
Для каждого субъекта рейтинговая оценка будет иметь свое распределение вероятностей. Усреднение таких оценок может приводить к значительным искажениям. Для исключения этого нужен инструмент определения соответствия значений случайных величин с разными распределениями. Для непрерывных величин X и Y можно использовать функцию:
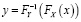
где F – функция распределения соответствующей случайной величины. Для дискретных случайных величин такой подход не является точным. Идея следующего метода связана с сопоставлением значений двух вариационных рядов с одинаковыми номерами. Для дискретных случайных величин в вариационном ряду одинаковые значения образуют интервал. Сопоставление компонентов вариационных рядов приводит к ситуации, когда интервалу одинаковых значений x будет соответствовать часть вариационного ряда для Y, возможно, с неодинаковыми значениями y. Если вместо вариационных рядов использовать вероятности, то получается следующая схема. Значению x соответствует (рис. 1) интервал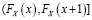 
. Этому интервалу могут соответствовать несколько значений Y:
,
.
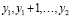
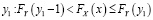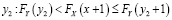Значению x можно поставить в соответствие среднее значение y из интервала, соответствующего интервалу (FX(x), FX(x+1)). Определим случайную величину Z на основе распределения Y:
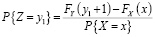
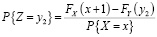
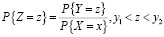
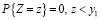или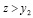 
Значению x ставится в соответствие M[Z].
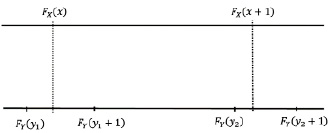
Рис. 1. Соответствие двух шкал на основе сопоставления функций распределения FX(x) и FY(y)
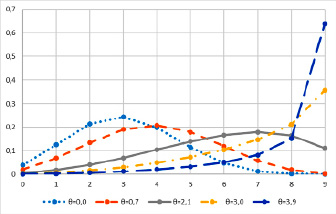
Рис. 2. Распределения вероятностей оценок с одинаковыми латентными параметрами объектов и разными параметрами θu субъектов
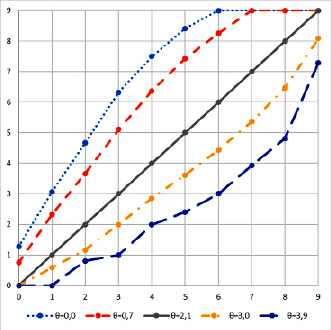
Рис. 3. Преобразование оценок с распределениями для разных параметров θu к распределению θu = 2,1
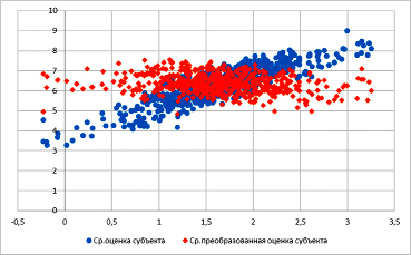
Рис. 4. Разброс усредненных исходных и преобразованных оценок субъектов в зависимости от значений латентного параметра субъекта
Преобразование оценки на основе разности распределений следует проводить для исключения тенденции субъекта ставить завышенные или заниженные оценки. Такая тенденция субъекта определяется его латентным параметром: чем больше параметр θu субъекта, тем больше вероятность высокой оценки (рис. 2).
На рисунке 3 приведены преобразования оценок с разными распределениями, ось ординат соответствует исходным оценкам, ось абсцисс – преобразованным. Как было естественно ожидать, преобразование увеличивает оценки субъектов с низким значением латентных параметров – склонных занижать оценки – и уменьшает оценки субъектов с большими значениями латентных параметров – склонных завышать оценки. Пилообразность преобразования для θu = 3,9 объясняется неравномерным перекрытием интервалов, соответствующих одинаковым значениям случайных величин с разными распределениями вероятностей.
На рисунке 4 представлена диаграмма разброса исходных и преобразованных оценок в зависимости от значений латентного параметра субъекта. Диаграмма демонстрирует, что преобразование компенсирует смещение оценок под влиянием тенденции субъекта завышать или занижать оценки.
Выводы
Предложенная модель рейтинговых оценок позволила построить вероятностные распределения рейтинговых оценок в зависимости от свойств субъектов и объектов, задаваемых латентными параметрами. Результаты обработки большого множества наблюдений подтверждают адекватность модели. Полученные распределения позволили определить преобразование оценок на основании распределения вероятностей рейтинговой оценки и усредненного распределения. Такое преобразование позволяет исключить субъективность оценок. В предложенную модель можно включить дополнительные параметры субъектов и объектов оценивания для учета факторов, которые могут повысить точность моделирования. Применение предложенной методики пересчета оценок позволяет получить более объективные оценки и более точные рейтинги объектов.