Рассмотрим массообмен около сферической капли при наличии объемной химической реакции. Концентрация в потоке удовлетворяет уравнению (см., напр., [1], гл. 5, (6.1)–(6.3)):
∆C=Pe (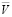
, 
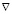)C + kv F(C), (1)
где Pe – число Пекле, kv – постоянная скорости химической реакции. Поле скоростей жидкости вне сферической капли определяется из выражений ([2], стр. 73):
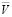=(vr, vθ, v0),
vr =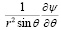
, vθ = 
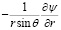, (2)
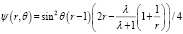, (3)
где ψ(r, θ) – функция тока. Требуется построить а.р. решения уравнения (1) при граничных условиях:
C = 1 когда r = 1; C → 0 для r → ∞. (4)
Процесс массообмена тонкой капли в потоке исследован в работе [3], массообмена между каплей или пузырьком в изотропном турбулентном потоке – в [4], массоперенос вокруг тонкой капли в нелинейном продольно-ползучем течении – в [5], массоперенос вокруг сферических пузырьков, капель и твердых частиц в одноосных и двухосных нелинейных ползущих течениях – в [6], массообмен вокруг сферической капли двойной эмульсии в однородном ползучем потоке и при больших числах Пекле – в [7], точные решения уравнений конвективной диффузии с переменными коэффициентами – в работе [8]. А классы нелинейных уравнений массообмена с переменными коэффициентами, решенные с функциональным разделением переменных, исследованы в работе [9].
Особенность задачи (1), (4): 1) величина μ0 = kv / Pe – постоянная и 2) Pe → ∞. При таких же предположениях, но в случае, когда функция F(C) удовлетворяет условиям F(0) = 0, F’(0) > 0, а.р. решения внутри капли построено в работе [10], вне капли построено в работе [11]. В этих случаях асимптотики носят степенной характер.
Заметим, что в случае, когда F(0) = 0, F’(0) > 0, главный член разложения функции F(C) при С → 0 носит линейный характер.
В данной работе предполагается, что:
F: R1→ R1, F(0) = 0, F'(0) = 0, 0 < F"(u) (5)
и справедливо представление:
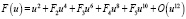, (6)
При u → 0. В этом случае главный член разложения имеет квадратичную структуру, что приводит к появлению медленно убывающих членов по пространственной переменной логарифмического типа на бесконечности.
Цель работы: исследовать задачу (1), (4) в малой окрестности капли: сначала строится асимптотика по ε = (Pe)–1/2, затем строится асимптотика на бесконечности по пространственной переменной как решение обыкновенного дифференциального уравнения. Для исследования асимптотики используется Maple.
Новизна работы состоит в том, что построено а.р. решения на бесконечности по пространственной переменной в диффузионном пограничном слое около капли. Затем методом согласования а.р. получено решение в эллиптическом пограничном слое. Полученные а. р. используются для численного моделирования решения около границы.
Диффузионный пограничный слой
Уравнение (1) с учетом обозначений ε = (Pe)–1/2 и μ0 = kv / Pe перепишем в виде:
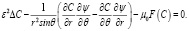(7)
В диффузном слое переходим к переменным t = ε–1(r – 1), θ. Асимптотическое разложение решения ищется в виде ряда:
c(t,θ,ε) = c0(t,θ) + εc1(t,θ). (8)
Функцию F(C), а также функцию тока ψ заменим главными членами разложения в окрестности c0(t,θ). Тогда для главного члена c0(t,θ) в области 0 < θ < π, 0 < t получается уравнение:
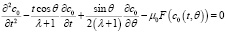, (9)
и условия
c0(0,θ) = 1; c0(t,θ)→0 при t→∞,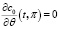 
. (10)
Асимптотическое разложение для c0(t,θ) при θ →0 строится в виде:
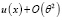, (11)
где x =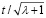 
. Из уравнения пограничного слоя (9), при малых θ относительно u(x) получаем:
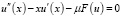, (12)
где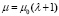 
, учитывая условия (10), находим:
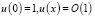при x → ∞. (13)
Основной результат в этом пограничном слое состоит в следующем.
Теорема. Предположим, что выполнены условия (5), (6). Тогда найдется μ1 > 0 такое, что при всех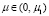 
решение задачи (12), (13) при x → +∞ имеет а.р.
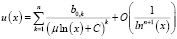(14)
для некоторого C, где:
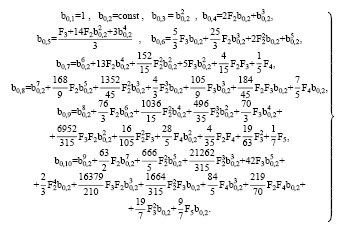(15)
Справедливы неравенства u > 0, u < 0 при x > 0. Такое решение единственно в классе ограниченных функций.
Доказательство теоремы. Сначала строится асимптотическое решение вида (14). Коэффициенты разложения находим, применяя метод неопределенных коэффициентов в среде Maple. Особенность задачи состоит в том, что структура асимптотики носит медленно убывающий характер на бесконечности. Приходится строить достаточное число членов асимптотики. Сперва в программе Maple наберем частичную сумму ряда порядка n (n = 10 ) :
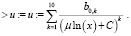(16)
Вычислим производную данного ряда:
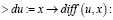
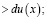
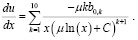(17)
Вторая производная ряда имеет оценку порядка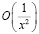 
, поэтому ее не будем учитывать. Сохраняем лишь медленно убывающие члены. Находим степень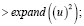 
и находим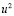 
, затем после каждой операции удаляем степени выше 11.
Итак, находим:
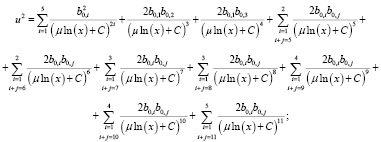
Так же вычисляются четвертая и шестая степени, опустим их вид в силу большого количества членов: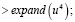 
: 
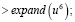далее находим:
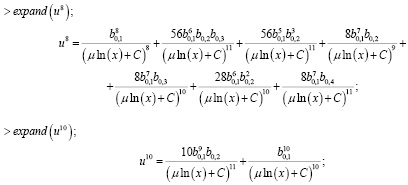
затем находим:
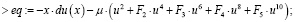
Далее находим p,
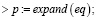
А затем находим коэффициенты (здесь приходится вводить для коэффициентов при одинаковых степенях новые обозначения):
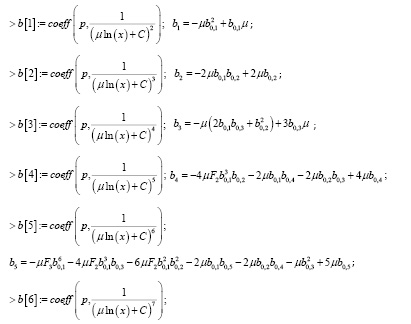
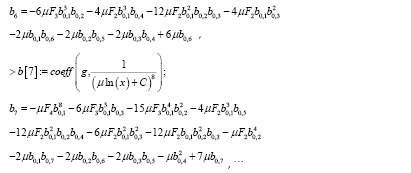
Далее получаем выражения для b8, b9, b10. Из полученных выражений, приравнивая к нулю, находим искомые коэффициенты:
Таким образом, продолжая аналогично, получаем справедливость выражений (15) для коэффициентов.
Итак, построено формальное асимптотическое разложение решения порядка n (n =10). С учетом медленного убывания слагаемых ряда и в целях численного моделирования приходится находить достаточное количество слагаемых. Далее обоснование формальной асимптотики доказывается так же, как и в теореме 1 работы [11].
Область задней критической точки
В этом пограничном слое решение строится в переменных
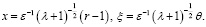
Для главного члена асимптотики получаем уравнение:
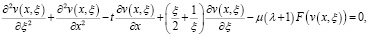(18)
и условия:
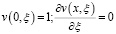при 
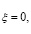(19)
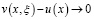при х → +∞ (20)
Из теоремы, рассмотренной выше, получаем, что функция u(x) удовлетворяет условиям (18) – (20).
Численное моделирование
Переходим к численному моделированию решений задачи (12), (13). В а. р. (15) есть произвольная константа b0,2. Это дает возможность удовлетворить граничным условиям (13). Уравнение (12) перепишем в виде системы:
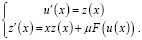(21)
Функцию F(u(x)) перепишем в виде суммы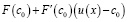 
. Начальные условия получим, пользуясь теоремой:
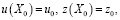(22)
где постоянные u0, z0 определяются из выражения (16) и ее производной (17), например в точке X0 = 150.
Для определения постоянной b0,2 выбираем промежуток (a,b), например a = 0.01, b = 20. Далее постоянная b0,2 находится методом половинного деления, при этом требуется выполнение граничного условия u(0) = 1.
Рассмотрим случай, когда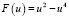 
. Методом Эйлера получены следующие результаты, например:
μ = 0.5, u = 1.0000; z = –0.8468; C = 0.9626, μ = 1, u = 1.0000; z = –0.8891; C = 0.2435;
μ = 2, u = 1.0000; z = –0.9286; C = 0.6043, μ = 3, u = 1.0000; z = –0.9657; C = 1.6021.
Заключение
В работе показано, что а.р. решения в диффузионном пограничном слое на бесконечности по пространственной переменной имеет логарифмическую структуру. Методом согласования а.р. решений диффузионного и эллиптического пограничных слоев в промежуточном пограничном слое получена аналогичная структура в эллиптическом слое.
Заметим, что в работе проведено математическое моделирование процесса массообмена методом согласования а.р. в двух пограничных слоях, описаны этапы программного построения а.р. с использованием программы Maple. Затем полученные результаты использованы для разработки алгоритма численного метода решения краевой задачи. Работа представляет теоретический интерес в области математической физики, а также практически может быть использована в химической технологии при анализе процесса массообмена около капли.