Актуальность статьи определяется расширением сферы возможного применения тенсионных устройств (ТУ) в современном мире, а также их разнообразием и сложностью их конструкций.
Цель исследования состоит в дальнейшем научном развитии авторского направления [1] математического моделирования ТУ и в содействии расширению их сферы применения. Достижение данной цели планируется путем решения двух задач: задача 1 – расширение сферы моделирования на все широко распространенные в настоящее время типы конструкций ТУ: блочные луки с падающей полочкой и с волосяной полочкой; традиционные английские луки; рекурсивные луки; блочные и рекурсивные арбалеты; задача 2 – обоснование расширения сферы применения ТУ в настоящее время.
Материалы и методы исследования
Обсуждаемое исследование началось с накопления материалов по практической стрельбе непосредственно авторов настоящей статьи из луков и арбалетов. Такой образ действий поддерживается современным российским законодательством [2, 3], где постепенно сокращаются ограничения на приобретение, хранение, применение луков и арбалетов. Далее применение метода теоретического обобщения этих материалов и метода их анализа привело к появлению нескольких новых авторских понятий, относящихся к предметной области: P – запасенная при натяжении тетивы потенциальная энергия; F(S) – кривая упругости ТУ; mred – приведенная масса ТУ; kfri – коэффициент трения стрелы о свою опору на ТУ и других. Понятие кривой упругости ТУ было заимствовано у А. Шалыгина [4]. Затем методом синтеза на базе этих понятий была получена математическая модель блочного лука с падающей полочкой. Модель использовала разнообразный математический аппарат, включая абстрактные метрические пространства, теорию меры, интегралы Лебега, но получилась относительно несложной. Авторы статьи преподают в вузах различные дисциплины из областей математики и информатики, применяя подобные свои модели [5, 6] как учебный материал. Метод совершенствования указанной выше модели позволил распространить ее на все широко распространенные в настоящее время типы конструкций ТУ. В статье [1] был необходим обзор мировых научных достижений в области математического моделирования ТУ. Методы сбора, анализа и обобщения соответствующего материала привели к следующему: 1) на основе изученных материалов (опубликованных в открытой печати) можно выделить два различных направления (две группы подходов) к математическому моделированию ТУ, которые с нашим подходом почти ничего общего не имеют; 2) подход авторов настоящей статьи представляет собой третье оригинальное направление; 3) никакое из упомянутых выше трех направлений, ни они в совокупности не могут полностью обеспечить научную поддержку производства современных луков и арбалетов. Вероятно, существуют значительно более развитые математические модели современных луков и арбалетов, не представленные в открытой печати.
Цель функционирования ТУ – это разгон стрелы. Скорость стрелы varr(t) зависит от времени. При t = 0 спускается тетива, varr(0) = 0. В момент t* отрыва стрелы от тетивы ее скорость – это varr(t*). Она зависит лишь от особенностей конкретного ТУ и от массы стрелы marr – чем меньше marr, тем больше varr(t*). Поэтому модель расчета varr(t*) и является моделью ТУ. Разгон стрелы обычно занимает менее 1 с, поэтому здесь можно пренебречь аэродинамической формой стрелы, ветром, сопротивлением воздуха. По мнению авторов настоящей статьи, выстрел – это явление, которое наблюдается после разгона стрелы, а при его изучении важны аэродинамическая форма стрелы, ветер, сопротивление воздуха, важно и значение varr(t*), а какое именно устройство разогнало стрелу – здесь уже не важно. Однако в некоторых источниках алгоритм расчета varr(t*) называют моделью выстрела из лука.
Идеи 2001–2016 гг. I. Zanievski, J.L. Park, M. Tiermas и др. [7–9] формируют хронологически первое направление. Здесь входные данные – это длины различных элементов лука, их массы, углы между ними, характеристики конструкционных материалов лука: прочность на растяжение, на изгиб, на кручение, величины упругих и пластических деформаций и пр. Далее изучаются взаимодействия между элементами лука в динамике по времени t. Получается система обыкновенных дифференциальных уравнений второго порядка по t, содержащая около десятка неизвестных функций и столько же уравнений, varr(t) – одна из этих функций.
Идеи 2008–2021 гг. А.В. Звягина, А.А. Лужина и др. [10, 11] формируют хронологически второе направление. Здесь входные данные – это тоже длины различных элементов лука, их массы, углы между ними, характеристики конструкционных материалов лука, но к ним добавляются также механическая работа и различные виды энергии. Последнее обстоятельство могло бы понизить размерность задачи. Однако получилась система дифференциальных уравнений 2 порядка в частных производных, содержащая 7 уравнений и 7 неизвестных функций. Частные производные берутся по двум параметрам, включая t – время. Также получается система обыкновенных дифференциальных уравнений второго порядка, содержащая 3 уравнения и 3 неизвестных функции.
Третье направление (авторов статьи) использует закон сохранения энергии, что позволило полностью исключить временную динамику из модели. Суммарная энергия системы «ТУ – стрела» при t = 0 и при t = t* одинакова. Очевидно, что varr(0) = 0, а нам надо вычислить varr(t*), поэтому ниже мы будем писать varr вместо varr(t*).
Результаты исследования и их обсуждение
1. Классификация тенсионных устройств для моделирования
На рис. 1, A, на примере некоторого ТУ показан смысл двух величин для тетивы: S (длина натяжения) и F (сила натяжения).
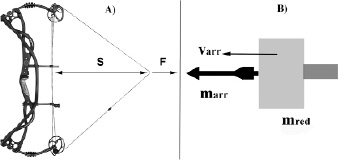
Рис. 1. A) Блочный лук: S – длина натяжения; F – сила натяжения; B) Механическая модель ТУ
Натягивая тетиву постепенно, можно построить график зависимости F(S) – кривую упругости ТУ. Пусть Smax – это то значениe S, при котором стрелок спускает предварительно натянутую тетиву. Принцип 1 классификации: либо ТУ имеет фиксированное (одинаковое) значение Smax для каждого выстрела, либо нет. Fmax – это максимальное значение функции F(S) на отрезке [0; Smax]. Принцип 2 классификации: либо при моделировании ТУ можно пренебречь трением стрелы о него, либо нет. Комбинируя оба принципа, получаем 4 типа ТУ: тип 1 – это блочные луки с падающей полочкой (Smax – фиксирована, трением стрелы пренебрегаем); тип 2 – это блочные луки с волосяной полочкой и все арбалеты (Smax – фиксирована, трение стрелы учитываем); тип 3 – это традиционный английский лук и все рекурсивные луки (Smax – не фиксирована, трение стрелы учитываем), тип 4 – содержит не обсуждаемые в статье рогатки (Smax – не фиксирована, метательный снаряд трется только о воздух, чем можно пренебречь).
2. Моделирование тенсионных устройств различных типов
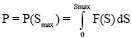 . (1)
. (1)
Используя (1), для типов 1 и 2 (Smax – фиксировано) нужно численным интегрированием получить значение параметра P (потенциальная энергия, запасенная при натяжении тетивы). Для типа 3 (Smax – не фиксировано) параметром является функция P(Smax) для любого Smax ∈ [0; SmaxDoc], где SmaxDoc – максимальная длина натяжения тетивы по документации для данного ТУ. В последнем случае можно, например, использовать для P(Smax) кубические сплайны, построенные по некоторой таблице аргументов и значений этой функции. На рис. 1, B, показана механическая модель, которая лежит в основе нашей математической модели: стрела массой marr разгоняется поршнем массой mred до скорости varr, после чего поршень останавливается. Приведенная масса mred ТУ – это масса поршня, который этому ТУ эквивалентен. Ниже приведено доказательство того, что любое ТУ может адекватно моделироваться таким образом.
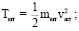
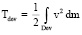 . (2)
. (2)
Для (2) Tarr – кинетическая энергия стрелы при покидании ТУ; Tdev – кинетическая энергия всех движущихся частей ТУ, дается интеграл Лебега по ТУ Dev, которое состоит из малых элементов массы dm, каждый из которых имеет свою скорость v.
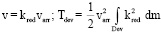 , (3)
, (3)
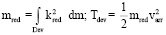 . (4)
. (4)
Для (3): если бы стрела полетела вдвое быстрее, то и всякая точка тетивы, например, тоже двигалась бы вдвое быстрее. Для всякого элемента ТУ массой dm существует kred – коэффициент пропорциональности между скоростями v этого элемента и varr. Отсюда формула для Tdev из (3). Входящий в нее интеграл Лебега зависит лишь от конструкции ТУ. (4) доказывает адекватность механической модели (рис. 1, B).
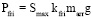 , (5)
, (5)
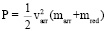 , (6)
, (6)
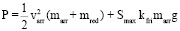 , (7)
, (7)
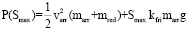 .(8)
.(8)
Pfri из (5) – это часть P для противодействия силе трения стрелы по закону Амонтона – Кулона, где kfri – коэффициент трения, g – ускорение свободного падения. Из (1)–(5) и закона сохранения энергии получаем (6)–(8) для ТУ типов 1–3 соответственно.
3. Подход к вычислительному эксперименту на основе выстрелов
Из изучаемого ТУ производим 2–3 выстрела различными по массе стрелами и замеряем их скорости. Используя эти данные, находим ключевые характеристики этого ТУ. Они позволяют по любой массе стрелы аналитически определять ее скорость.
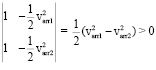 . (9)
. (9)
Формула (6) действительна только для ТУ типа 1, там рассмотрим величины P, mred как неизвестные, а остальные – как известные. Отсюда линейное уравнение с двумя неизвестными. Производим два выстрела стрелами массами marr1 < marr2, замеряем их скорости varr1 > varr2. Получаем линейную систему двух уравнений с двумя неизвестными с ненулевым (9) главным определителем. Находим неизвестные P, mred. Зная их и используя (6), для произвольной стрелы массой marr мы можем найти varr. Отсюда ТУ типа 1 описывается P, mred.
 . (10)
. (10)
Формула (7) действительна только для ТУ типа 2, там рассмотрим P, mred, kfri как неизвестные, а остальные – как известные. Получим линейное уравнение с тремя неизвестными. Делаем три выстрела стрелами массами marr1 < marr2 < marr3, замеряем соответствующие скорости стрел varr1 > varr2 > varr3. Получаем линейную систему трех уравнений с тремя неизвестными. Ее главный определитель (10) может быть и нулевым в принципе, тогда будем брать стрелы с другим набором масс. При ненулевом главном определителе (10) мы находим неизвестные P, mred, kfri. Зная их и используя формулу (7), для произвольной стрелы массой marr мы можем найти varr. Отсюда ТУ типа 2 описывается P, mred, kfri, Smax. Для ТУ типа 3 метод не работает.
4. Подход к вычислительному эксперименту на основе кривой упругости и выстрелов
Из (1) для ТУ типов 1 и 2 численно определяем P, для ТУ типа 3 численно строим функцию P(Smax). Из ТУ типа 1 стрелой массой marr делаем один выстрел, замеряя varr. Используем (6), где теперь только mred – неизвестная. Находим ее.
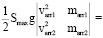
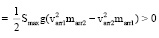 , (11)
, (11)
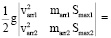
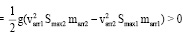 .(12)
.(12)
Для ТУ типов 2 и 3 делаем два выстрела соответственно стрелами с массами marr1 < marr2. Замеряем соответственно varr1, varr2. Для ТУ типа 3 также берем Smax1 ≈ Smax2. Затем для ТУ типа 2 используем (7). Имеем линейную систему двух уравнений с двумя неизвестными mred и kfri. Из (11) – ее главный определитель положителен для ТУ типа 2. Находим эти неизвестные. Формула (8) действительна только для ТУ типа 3, где P и varr зависят от Smax. Два выстрела дают для ТУ типа 3 аналогичную линейную систему. Из (12) – ее главный определитель положителен для ТУ типа 3. Находим mred и kfri. Из (8) для произвольных marr, Smax найдем varr. ТУ типа 3 описывается: функцией P(Smax) и числами mred, kfri.
5. Кривая упругости для различных тенсионных устройств
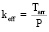 , (13)
, (13)
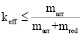 , (14)
, (14)
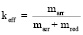 . (15)
. (15)
Формула (13) определяет keff (коэффициент полезного действия). (13) влечет (14). (15) действительна только для ТУ типа 1.
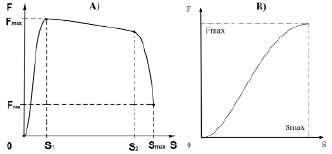
Рис. 2. Кривая упругости F(S): A) для блочных луков и блочных арбалетов; B) для традиционного английского лука Long Bow

Рис. 3. Основные виды традиционных луков в боевом положении – тетива не натянута: A) монгольский лук; B) турецкий лук; C) Long Bow
Для ТУ многое определяется его кривой упругости F(S) при S ∈ [0; Smax]. ТУ тем лучше, чем для него больше запасенная при натяжении тетивы Р, вычисляемая из (1).
Pmax = Fmax*Smax, (16)
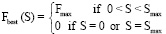 . (17)
. (17)
Пусть Fmax и Smax – это максимум конкретного стрелка, тогда (16) дает теоретически максимальное значение P. F(0) = 0 для любого ТУ. Если F(Smax) = 0, то для удержания максимально натянутой тетивы нужно минимальное (нулевое) усилие стрелка (в случае лука) и замка тетивы (в случае арбалета). Формулы (1) и (17) дают Fbest(S) для теоретически самого лучшего ТУ. Его практическая реализация невозможна.
kint = P/Pmax. (18)
Формула (18) определяет kint. Очевидно 0 < kint < 1, следовательно, kint – показатель близости ТУ к идеальному. На рис. 2, А, рассмотрим кривую при S на промежутках: от 0 до S1, от S1 до S2, от S2 до Smax, где Fmax = F(S1), F(Smax) = Fres, Fres<< Fmax – на блочном луке прицеливание происходит при небольшом усилии стрелка, для этого лука 0,85 < kint < 0,95, 1 и 3 промежутки на рис. 2, A, показаны бо́льшими (для наглядности), чем они на самом деле. Из (17) для блочного лука F(S) близка к Fbest(S).
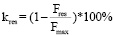 . (19)
. (19)
Только для блочных луков (19) определяет kres – коэффициент сброса усилия стрелка при прицеливании. Обычно 60 % ≤ kres ≤ 90 %.
Из рис. 3, C, видно, что плечи традиционного английского лука (Long Bow) состоят из одной дуги, поэтому степень рекурсивности этого лука rL = 1 – такие луки рекурсивными не считаются. Аналогично, из рис. 3, B, для турецкого лука rT = 3, из рис. 3, A, для монгольского лука rM = 5 – такие луки называются рекурсивными. Степень рекурсивности r = 5 также имеют луки: индейские, скифские, татарские, арабские, корейские, казахские, башкирские, славянские, венгерские и другие – большинство народов пришло именно к таким традиционным лукам. Чем выше r, тем выше keff.
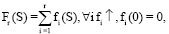
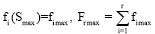 . (20)
. (20)
На рис. 2, B, показана функция F(S) для Long Bow. Она гладкая, монотонно возрастает, F(0) = 0, F(Smax) = Fmax. Для любой дуги плеч рекурсивного лука она будет по сути такой же. Формула (20) дает (с учетом r) зависимость Fr от S. Здесь fi – сила натяжения дуги i, вместо Fmax для fi и Fr используются fi max и Fr max соответственно. Из-за нескольких разгонных импульсов для стрелы на графике Fr(S) появляется несколько гладких ступенек.
6. Особенности применения тенсионных устройств
ТУ отличаются пожарной безопасностью, малошумностью, разнообразием типов метательных снарядов. Из-за последнего альпинисты применяют арбалеты для транспортировки небольших грузов. Аналогично можно было бы поступать при монтаже высотных конструкций, управлении парусным судном, ускорении летательных аппаратов при взлете. Если на базе современных технологий построить аналоги древних мощных арбалетов, то эта сфера применения существенно расширится. Выстрел из огнестрельного оружия вблизи пожароопасных объектов может привести к техногенной катастрофе. Для их охраны целесообразно пользоваться арбалетами и даже луками из-за их большей скорострельности. В России [2] луки и арбалеты могут быть не оружием, а средствами для спорта и развлечений. Стрельба из лука и арбалета увлекательнее, чем занятия с гантелями, а эффект для мышц рук аналогичен. Некоторые заболевания исключают занятия с гантелями, но не занятия с луком и арбалетом. В США охотники, применяющие арбалеты и луки [4] для охоты на крупных хищников, всегда вооружены также мощным револьвером или пистолетом в качестве оружия «последнего шанса» – там это обязательное правило охоты. В России [2] короткоствольное огнестрельное оружие (кроме травматического) в принципе не может быть гражданским, а следовательно, и охотничьим. Охота с луком и арбалетом [2, 3] с 2020 г. в России разрешена. Думается, это противоречие должно быть устранено.
Заключение
Поставленные выше задачи 1 и 2 решены, цель исследования (дальнейшее научное развитие авторского направления математического моделирования ТУ и содействие расширению их сферы применения) достигнута.



