В машиностроении распространение получили приводы машин, состоящие из механизмов, которые включают в себя узлы, соединяющие двигательные и исполнительные устройства между собой. Узлы механизмов, как правило, содержат механические передачи редукторного типа. Одной из разновидностей таких передач являются простые зубчатые цилиндрические передачи, которые состоят из шестерни и колеса, причем основной их задачей является передача вращающего момента шестерней колесу с понижением частоты вращения колеса из-за наличия передаточного отношения. Работа таких передач осуществляется под действием нагрузок, которые вызывают упругие деформации элементов привода.
Учет упругих деформаций является важной задачей на этапе проектирования, так как они влияют на правильную работу механизма, например в зубчатых передачах приводят к неравномерности распределения усилий по контактной линии сопряженных зубьев, шуму, к недостаточной приработке зубьев, различным колебаниям и пр. Расчет всех возможных упругих деформаций элементов привода классическими методами – достаточно трудная задача [1], поэтому обычно рассчитывают только деформации изгиба зубьев, кручения ободьев или тел колес и изгиба валов. В статье [2] авторы рассмотрели возможности топологической оптимизации при проектировании зубчатых шестерней с получением жестких конструкций меньшей массой на 10–18% по сравнению с колесами, получаемыми традиционными методами. В работе [3] авторы разработали рекомендации по наблюдению за зубчатыми колесами с помощью анализа НДС в ASNSYS их твердотельных геометрических моделей без необходимости демонтажа. Авторы в источнике [4] при анализе действующей нормативно-технической документации выявили отсутствие единых подходов к оценке технического состояния зубчатых передач при проведении экспертизы надежности, в том числе учитывая возможные деформации и другие факторы, влияющие на их работу. В статье [5] приведен анализ напряжений и деформаций зубчатых колес из различных материалов без учета формы тела колеса, с целью замены широко применяемых материалов композитными. Оценка НДС колес с целью предупреждения и выявления на ранней стадии проектирования областей, в том числе в труднодоступных местах (например, диск и ступица колеса), без их демонтажа, с высокими концентрациями напряжений или деформаций является на сегодняшний момент актуальной задачей, так как позволяет повысить технологичность изделия, минимизировать издержки эксплуатации и предотвратить преждевременные поломки. Выполнение задач подобного типа на этапе проектирования можно осуществить на основе использования МКЭ алгоритмов, которые могут поставляться как отдельный комплекс САЕ расчетов (ANSYS и др.), так и быть встроенными САЕ модулями в СAD системы, например: Компас 3D APM FEM, SOLIDWORKS Simulation, T-Flex CAD Анализ.
В статье рассматривается влияние формы и положения диска зубчатого колеса с помощью МКЭ алгоритмов на напряжения и деформации колеса, в том числе в зоне сопряженных зубьев в статической постановке, что позволяет снизить трудоемкость работы конструкторов при выборе рационального варианта конструкции зубчатого колеса, так как такие расчеты можно выполнить без экспериментальных данных, а предлагаемый вариант исследования может быть применен на практике.
Цель исследования – оценить, как форма диска и его положение относительно плоскости симметрии зубчатого колеса, которая делит пополам его венец по ширине, влияют на НДС в различных областях этого колеса, с целью выбора из представленных в статье конструкций колес, обладающих высокой прочностью, технологичностью изготовления.
Материалы и методы исследования
Из многообразия возможных вариантов конструкций цилиндрических зубчатых колес выбраны пять различных типов, которые отличаются формой и положением диска, а также являются распространенными в общем машиностроении, причем в двух типах рассматриваются три разные толщины диска при одинаковой форме. Всего в исследовании участвуют девять различных вариантов зубчатых колес (рис. 1), каждое из которых сопряжено с простой по конструкции шестерней.
Геометрические параметры тел (венца, диска, ступицы) зубчатых колес приняты на основании рекомендаций в классической литературе [6], причем точные по форме твердотельные модели построены в программе КОМПАС-3D [7] с помощью встроенных библиотек, где конструктивные параметры зацепления определены в соответствии с ГОСТ 16532–70. Зубчатая передача – прямозубая, число зубьев шестерни z1 = 18 шт., колеса z2 = 45 шт., модуль m = 10 мм. Нормальный исходный контур принят согласно ГОСТ 13755-2015. Ширина зубчатой шестерни bw1 = 130 мм, колеса bw2 = 130 мм. Передаточное число u = 2,5. Межосевое расстояние aw = 315 мм. Диаметр вершин зубьев шестерни da1 = 200 мм, колеса da2 = 470 мм. Угол зацепления αtw = 20°, колеса выполнены без смещения инструмента. Посадочный диаметр отверстия шестерни 70 мм, ступицы колеса dk = 100 мм, острые кромки притуплены фаской z = 2,5 мм. Размеры шпоночных пазов приняты в соответствии с ГОСТ 23360-78. Диаметр ступицы колеса dst = 150 мм. Внутренний диаметр обода колеса ds = 377 мм. Диаметр расположения центров отверстий в диске колеса dc = 264 мм, диаметр отверстий в диске do = 45 мм. Отверстий в диске предусмотрено восемь штук, но в третьем варианте колеса (рис. 1) из-за наличия ребер жесткости – шесть штук, острые кромки в отверстиях диска во втором и третьем вариантах колеса притуплены скруглениями радиусом 2 мм. На торцах зубчатого венца (зубьях и углах обода), а также на торцах ступицы предусмотрены фаски f = 4 мм. В колесе № 1 (рис. 1) толщина диска 122 мм, что на две величины фаски f меньше ширины bw2. В колесе № 2 диск имеет торообразные симметричные кольцевые выточки с двух сторон, причем в наименьшем сечении диска его толщина равна C2 = 46 мм, что составляет 0,35bw2. В колесе № 3 диск имеет наклон в 10°, отстоит от левого торца ступицы на 9 мм, толщина его C2 = 0,2bw2 = 26 мм, шесть равномерно расположенных ребер жесткости имеют толщину t = 21 мм.
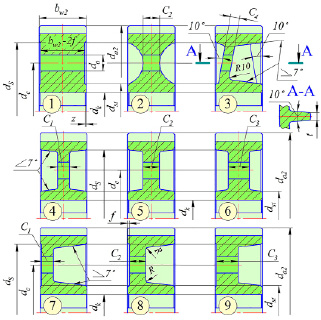
Рис. 1. Девять различных вариантов исследуемых по конструкции зубчатых колес
В колесах № 4, 5, 6 диск симметрично расположен относительно плоскости симметрии зубчатого колеса, которая делит пополам его венец по ширине, имеет толщину, равную C1 = 33 мм, что составляет 0,25bw2, C2 = 46 мм, C3 = 59 мм или 0,45bw2 соответственно. В колесах № 7, 8, 9 диск расположен несимметрично, отстоит от левого торца колеса на величину фаски f, имеет толщину, равную C1 = 33 мм, C2 = 46 мм, C3 = 59 мм соответственно. Радиусы скруглений в местах перехода диска в обод и ступицу равны R = 6 мм, за исключением одного места в варианте № 3 (рис. 1). Шестерня и колесо изготовлены из конструкционной углеродистой качественной стали марки 50, имеющей предел текучести 530 МПа, предел прочности 760 МПа, твердость рабочих поверхностей 228–255 НВ, модуль упругости 2,16 ∙ 105, материал в расчетах принимается линейно-упругим, однородным, изотропным. Вращающий момент равномерно приложен к внутренней поверхности посадочного отверстия шестерни и к одной из граней шпоночного паза, равен T1 = 1142 Нм. Мощность, передаваемая шестерней, составляет 24 кВт.
Исследование численными методами НДС зубчатых колес (рис. 1) проведено в SOLIDWORKS Simulation [8]. В расчетах введены допущения, то есть не рассматриваются погрешности изготовления и монтажа зубчатой передачи, не учитываются форма и размеры валов и их опор, на которых закреплены зубчатые колеса, за исключением посадочных отверстий и прилегающих поверхностей, к которым приложены ограничения, отражающие реальную работу колес в механизме. Применены ограничения трех видов. Первое ограничение имитирует соосное расположение посадочного отверстия шестерни на ведущем валу и позволяет совершать ей поворот вокруг своей оси на 360 градусов, запрещая ей перемещения в двух взаимно перпендикулярных радиальных направлениях. Второе ограничение – это полное закрепление посадочного отверстия колеса и одной из граней шпоночного паза, что имитирует соосное расположение колеса относительно ведомого вала, а также силы производственного сопротивления при работе передачи. Третье ограничение ограничивает перемещения шестерни и колеса в осевом направлении, что имитирует установку смежных деталей, в том числе опор. Также применен ряд стандартных сопряжений, которые позволяют геометрически правильно расположить в трехмерном пространстве элементы зубчатой передачи друг относительно друга на заданном межосевом расстоянии. Для передачи вращающего момента от шестерни к колесу создано контактное ограничение для рабочих поверхностей боковых эвольвентных профилей зубьев в области их сопряжения без проникновения. Произведено построение тетраэдральной конечно-элементной сетки, причем размер сетки менялся от 1 до 5 мм, что позволило в местах плавных переходов в основании зубьев и скруглениях получить более мелкую сетку. В области сопряженных поверхностей зубьев передачи сетка была уменьшена до 0,5 мм, так как в этих местах предполагались большие градиенты напряжений. Число рассматриваемых объемных конечных элементов сетки по всем вариантам колес (рис. 1), включая шестерню, приведено в таблице 1.
Для принятых в исследовании параметров зубчатой передачи с учетом свойств материала определены расчетные и допускаемые контактные напряжения с помощью прикладных библиотек программного обеспечения КОМПАС-3D, в которых напряжения определяются в соответствии с ГОСТ 21354-87, а также с помощью программного обеспечения [9] по методике расчета зубчатых передач, используемой в литературе [10].
Результаты исследования и их обсуждение
Проведено исследование статической прочности с помощью МКЭ алгоритмов для девяти вариантов зубчатых передач с построением картины распределения напряжений, определением максимальных эквивалентных напряжений фон Мизеса (von Mises) и контактных давлений (СР) в зоне сопряженных поверхностей зубьев передач. Рассчитаны максимальные напряжения в теле диска с учетом переходных участков (скругления между диском со ступицей и ободом), а в третьем варианте – с учетом ребер жесткости. Вычислены моменты инерции колеса относительно оси вращения с его массой. Определены максимальные деформации в зоне контактирующих поверхностей зубьев передачи. Данные представлены на рисунках 2–4 и обобщенном графике (рис. 5). Для детальной оценки напряжений в диске зубчатого колеса и построения картины распределения напряжений (рис. 2–4) проведено зондирование его поверхностей с целью определения максимальной величины напряжений в каждом варианте. В седьмом варианте из всех рассмотренных напряжения в диске с учетом переходных участков достигают наибольших значений в 23 МПа, поэтому это значение на рисунках 2–4 принято в качестве промежуточного числа, которое разделило шкалу напряжений на две части – от 0 до 23 МПа и свыше 23 МПа, что позволило в каждом варианте использовать единую шкалу измерений напряжений для наглядности результатов.
В колесе по варианту № 1 (рис. 2, 5) в зоне контактирующих зубьев передачи деформации достигают минимальной величины в 11 мкм, эквивалентные напряжения в теле диска колеса незначительны и составляют 5,4 МПа, что является минимальным значением во всех вариантах, при этом его масса максимальна и равна 134 кг. Если необходимо колесо с высокой жесткостью, то предпочтителен вариант № 1 из рассмотренных. Колесо в варианте № 2 (рис. 2, 5) по уровню напряжений и контактных давлений сопоставимо с колесом № 6 (рис. 3, 5), но обладает на 6% большей массой и на 20% большими деформациями.
Колесо в варианте № 3 (рис. 2, 5) по уровню напряжений в диске сопоставимо с колесом № 9 (рис. 4, 5), но из-за большей величины деформаций и уровня напряжений в зоне контактирующих зубьев является менее предпочтительным, хотя и обладает на 10% меньшей массой. Колесо в варианте № 4 (рис. 3, 5) по уровню деформаций в зоне сопряженных зубьев сопоставимо с колесом № 3 (рис. 2, 5), но из-за наличия тонкого диска без ребер жесткости уровень напряжений в диске выше на 15%, что делает колесо № 4 предпочтительным, если необходимо выдержать примерно одинаковую толщину обода, диска и ступицы (рис. 1) при минимальной массе. Колесо № 5 (рис. 3, 5) по уровню деформаций в зоне контактирующих зубьев сопоставимо с колесом № 2 (рис. 2, 5), но обладает более высоким уровнем напряжений.
Таблица 1
Количество объемных конечных элементов сетки
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Количество элементов, млн |
2,7651 |
2,3489 |
2,3111 |
2,1404 |
2,2335 |
2,3382 |
2,1403 |
2,1838 |
2,3259 |
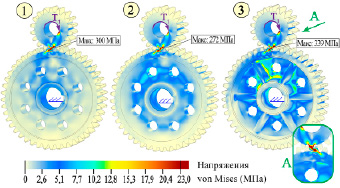
Рис. 2. Распределение напряжений в зубчатых передачах по вариантам № 1, 2, 3
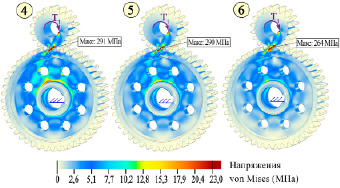
Рис. 3. Распределение напряжений в зубчатых передачах по вариантам № 4, 5, 6
Колесо в варианте № 7 (рис. 4, 5) является наименее предпочтительным как по уровню деформаций, так и по уровню напряжений и контактных давлений из-за несимметрично расположенного тонкого диска, который удален на максимальном расстоянии от плоскости симметрии зубчатого колеса, которая делит пополам его венец по ширине, причем наблюдается значительная неравномерность распределения уровня напряжений в зоне сопряженных зубьев. С точки зрения технологичности изготовления при невысокой массе предпочтительно использовать колесо в варианте № 8 (рис. 4, 5), хотя уровень эквивалентных напряжений и деформаций по сравнению с колесом № 5 (рис. 3, 5) выше.
Колеса с несимметричным расположением диска необходимо использовать в обоснованных случаях, так как на рисунках 2, 4 можно увидеть значительную неравномерность распределения эквивалентных напряжений по ширине зубьев в области их сопряжения и недостаточную жесткость венца колеса из-за увеличенных его деформаций (рис. 5).
На рисунке 5 приведен обобщенный график исследуемых параметров зубчатых колес, где по горизонтальной оси отмечены их номера, а по вертикальной – измеряемые значения.
Допускаемые и расчетные контактные напряжения, вычисленные с помощью прикладных библиотек КОМПАС-3D в соответствии с ГОСТ 21354-87, составляют 527 МПа и 414 МПа, с помощью программного обеспечения [9] – 473 МПа и 479 МПа соответственно.
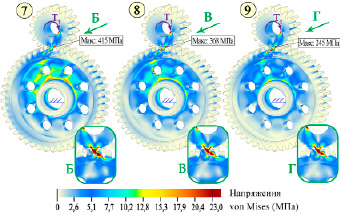
Рис. 4. Распределение напряжений в зубчатых передачах по вариантам № 7, 8, 9
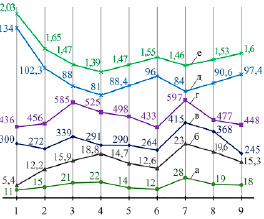
Рис. 5. Обобщенный график рассматриваемых параметров исследуемых передач: а – максимальные перемещения контактирующих зубьев передачи (мкм), б – максимальные эквивалентные напряжения в диске (МПа), в – максимальные эквивалентные напряжения в зоне сопряженных зубьев (МПа), г – максимальное контактное давление (СР) в зоне контактирующих поверхностей зубьев (МПа), д – масса колеса (кг), е – момент инерции колеса относительно оси вращения (кг·м2)
Сравнивая значения контактных давлений (CP) (рис. 5), полученных с помощью МКЭ алгоритмов, с контактными напряжениями, которые определены стандартными методами, можно подтвердить вышесказанные рассуждения по рисункам 2–4 и расположить колеса по мере предпочтительности НДС/массы. Наиболее близкие по значениям СР к расчетным значениям контактных напряжений по ГОСТ 21354-87 в колесе № 1, отличие в 5%, поэтому этот вариант конструкции колеса будем считать наиболее прочным и предпочтительным с точки зрения распределения НДС. Следующее колесо – № 5 (рис. 1, 5), СР меньше допускаемых по ГОСТ 21354-87 на 5,8%, деформации в зоне контактирующих зубьев незначительны, а конструкция колеса обладает на 34% меньшей массой и на 28% меньшим моментом инерции по сравнению с колесом № 1. Далее выделим колесо № 6, картина НДС лучше (рис. 3, 5), при этом наблюдается увеличение массы на 8% и на 5% – момента инерции по сравнению с колесом № 5. Потом колесо № 2 (рис. 2, 3, 5) – НДС близко к колесам № 5 и 6, но при сравнении с массой колеса № 5 видно ее увеличение на 14%, и на 11% больше момент инерции. Затем колеса № 9 и 8 (рис. 1, 4), так как из-за несимметричности расположения диска относительно плоскости симметрии зубчатого колеса, которая делит пополам его венец по ширине, распределение НДС по ширине колеса неравномерное, но они предпочтительны с точки зрения простоты изготовления, например в [9] рекомендуют использовать односторонние подкладные штампы и свободную ковку в сочетании с более толстой стенкой диска для снижения влияния термической обработки на геометрическую форму.
Заключение
В статье показано, что форма диска и его положение (рис. 1) относительно плоскости симметрии зубчатого колеса, которая делит пополам его венец по ширине, значительно влияют на НДС в различных областях этого колеса (рис. 2–5). Из рассмотренных девяти вариантов конструкций цилиндрических зубчатых колес для одного варианта сочетания геометрических параметров из множества возможных можно сделать вывод, что колесо № 1, имеющее простую конструктивную форму, является предпочтительным, так как обладает высокой прочностью и жесткостью (рис. 2, 5). Следует также предпочитать колеса с симметричным расположением диска толщиной более 35% от его ширины (варианты № 2, 5, 6, рис. 1–3, 5) из-за более равномерной картины распределения напряжений в зоне сопряженных зубьев, хотя они менее прочные и жесткие, но позволяют значительно снизить металлоемкость колеса. Технологичны в изготовлении колеса с несимметричным расположением диска толщиной более 35% его ширины (варианты № 8, 9, рис. 1), так как позволяют использовать простые методы их получения с экономией материала.
Предлагаемое исследование различных вариантов по конструкции зубчатых колес позволяет конструктору на стадии проектного расчета выбрать более рациональную форму, что в дальнейшем минимизирует издержки производства и эксплуатации, причем оценку НДС колес в зависимости от положения диска необходимо дополнять классическими методами расчета по различным рекомендациям и нормам.



