В настоящее время большинство методов обработки и анализа данных опираются на вероятностные методы. Характеристики вероятности задаются при помощи законов распределения, однако вид закона в случае работы с прикладными данными редко бывает известен заранее. Потому идентификация закона распределения вероятности является важной задачей, решение которой позволяет значительно повысить точность расчетов и прогнозов на их основе. В теории вероятности задача идентификации закона распределения вероятностей является обратной задачей, ключевой для математической статистики. Это определяет основную цель и направление математических изысканий в данной сфере.
Необходимо отметить, что процесс идентификации является достаточно сложным процессом. Примером тому может служить метод Парзена–Розенблатта [1], при использовании которого оценка ряда параметров является более трудоемкой задачей, чем собственно исходная задача идентификации распределения. Для упрощения идентификации закона распределения было разработано программное средство, получившее название «Knowlaw».
1. Принцип работы программного средства «Knowlaw»
В большинстве случаев для идентификации закона распределения используются какие-либо характеристики исследуемых совокупностей данных, которые позволяют выявить общие закономерности для формулирования закона распределения.
Ранее нами уже был представлен алгоритм, позволяющий идентифицировать законы распределения [2]. В его основе лежит ряд методов, позволяющих поэтапно отвергать законы распределения из общего их набора, которые не соответствуют тем или иным критериям. Среди таких методов выделены: определение непрерывности или дискретности исходных данных; определение моментов третьего и четвертого порядка – симметричности и плосковершинности искомого распределения; определение тяжести хвоста распределения; построение гистограммы и ее анализ. Кроме того, сформированная четкая последовательность действий позволяет подстраивать алгоритм под программный язык.
При этом каждый из указанных методов нуждается в проработке, что также было отражено в ряде ранее опубликованных работ. Метод определения непрерывности и дискретности исходных данных [3] основан на отборе повторов в совокупностях данных и обнаружении стандартного изменения каждой величины.
Другим методом является определение симметричности и плосковершиности распределений, для чего использовались коэффициенты асимметрии и эксцесса [4]. Отметим, что использование данных коэффициентов для идентификации законов распределения предлагалось и ранее [5], однако только для выделения нормального распределения из общего их числа. Общее количество идентифицируемых законов было определено посредством составления рейтинга, в котором учитывались отечественные и зарубежные работы, применяющие в процессе исследования те или иные законы распределения [6]. Примеров методов оценок тяжести хвоста достаточно много в современной научной литературе [7].
В качестве метода определения тяжести хвоста распределения для программного средства «Knowlaw» применялся метод, основанный на оценке Хилла [8]. Кроме того, в работе приведена адаптация данной оценки, поскольку ее базовый вариант не дает численного решения для задачи определения тяжести хвоста, что, в свою очередь, не дает возможности для идентификации закона распределения, и потому требует соответствующей доработки. Стоит отметить, что оценка Хилла является достаточно распространенной оценкой, применяемой в настоящее время [9].
Одним из наиболее распространенных методов, применяемых при идентификации закона распределения, является метод гистограмм [10]. Данный метод позволяет эксперту приблизительно оценить плотность распределения закона распределения, что дает возможность для приближенного принятия решения о виде закона распределения [11]. Как правило, гистограмма строится на основе ранжированного ряда распределения, количество столбцов гистограммы определяют при помощи формулы Стерджесса [12]. Подобные проверки также осуществляются различным набором методов, в большинстве случаев для этого применяется широко распространенный критерий Колмогорова [13].
Также для реализации метода применялся ряд коэффициентов, облегчающих принятие решения при оценивании распределения при помощи гистограммы [14]. Данные коэффициенты имеют в своей основе те же принципы, которые применяются в задачах распознавания образом. Полученные коэффициенты оценки гистограммы были проверены и на других работах, что подтверждает их адекватность и применимость [15].
Каждый из перечисленных выше методов имеет самостоятельное значение, однако их особенность заключается в том, что все они могут быть применены в комплексе [16]. Данная особенность создала предпосылки для разработки программного средства «Knowlaw».
Пример решения задачи идентификации закона распределения вероятности в данной программе приведен на рисунке.
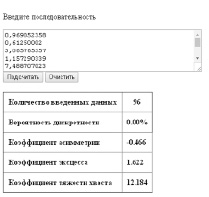
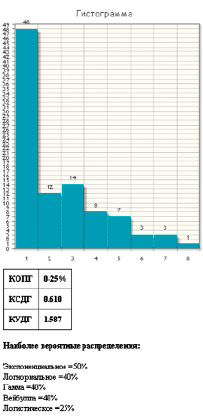
Пример решения задачи идентификации закона распределения вероятности в данной программе «Knowlaw»
Функционал программы включает в себя: расчет ряда коэффициентов (адаптированных для идентификации закона распределения); построение и анализ гистограммы посредством специально разработанных гистограммных коэффициентов; подбор решения на основе вероятностных характеристик появления у определенного закона распределения полученного набора результатов расчета каждого из коэффициентов.
Отличительной характеристикой программного средства является возможность его применения на достаточно малых выборках (от 10 наблюдений). Кроме того, решение принимается на основе комплексного анализа, и пользователю предлагаются также другие варианты, имеющие более низкую вероятность. Автоматизация процесса идентификации позволяет выбрать наиболее предпочтительный закон сразу из общего их количества.
2. Результаты проверки эффективности разработанной программы «Knowlaw»
Ниже приведем сравнение полученной программы с другими аналогичными программными средствами. Среди них в целях сравнения использовались модуль «Настройка распределения» в пакете Statistica, а также программа восстановления плотности «Обработка массивов данных», приведенная на сайте «Exponenta» [17]. В пакете прикладных программ Statistica имеется встроенная функция «Настройка распределения». Точность подгонки оценивается при помощи критерия Колмогорова, хи-квадрат, критериев Шапиро–Уилка и Лиллиефорса.
Образовательный математический сайт Exponenta.ru (http://www.exponenta.ru) имеет встроенный модуль «Обработка массивов данных», который предназначен для идентификации закона распределения. В программе имеется возможность идентификации таких законов распределения, как нормальный, экспоненциальный, равномерный непрерывный, треугольный, а также распределений Лапласа и Рэлея. Точность подгонки оценивается при помощи одновыборочного критерия Колмогорова или хи-квадрат Пирсона. Имеется возможность отображать гистограмму плотности распределения.
Сравним возможности каждого из перечисленных программах средств (табл. 1).
Согласно данным таблицы 1, авторское программное средство имеет ряд преимуществ перед другими программами. К этим преимуществам можно отнести заметно большее число законов распределения, которые удается идентифицировать, а также потенциальную возможность выбора определенного закона из нескольких схожих вариантов.
Таблица 1
Сравнение возможностей программных средств, применяемых для идентификации закона распределения
|
Критерии сравнения |
«Настройка распределения» |
«Обработка массивов данных» |
«Knowlaw» |
|
Количество различаемых распределений |
12 |
6 |
17 |
|
Минимальное количество данных |
3 |
25 |
10 |
|
Необходимость выбора распределения «вручную» |
Да |
Нет |
Нет |
|
Учет дискретных распределений |
Да |
Нет |
Да |
|
Возможность выбора из нескольких вариантов распределения |
Нет |
Нет |
Да |
Таблица 2
Величина ошибки первого рода в процессе идентификации законов распределения программными средствами, %
|
Сравниваемые распределения |
«Настройка распределения» |
«Обработка массивов данных» |
«Knowlaw» |
|
Нормальное |
4,5 |
5,5 |
5,0 |
|
Равномерное непрерывное |
4,5 |
4,0 |
3,5 |
|
Экспоненциальное |
3,5 |
6,5 |
4,5 |
|
Рэлея |
6,0 |
3,5 |
5,0 |
|
Среднее количество ошибок |
4,6 |
4,9 |
4,5 |
Далее проведем непосредственную оценку качества идентификации распределений. Поскольку каждое из приведенных программных средств может идентифицировать разное количество законов распределения, то остановимся только на тех из них, которые могут быть идентифицированы всеми тремя программами. Таким образом, среди всего многообразия законов распределения идентификации подлежат только нормальный, равномерный (непрерывный), экспоненциальный, а также распределение Рэлея.
Методика проверки следующая: на генераторе случайных чисел было сгенерировано множество совокупностей данных – 200 для каждого из распределений в интервале от 25, что составляет минимальный интервал для идентификации программой «Обработка массивов данных», до 1000 значений. В качестве генератора использовалась программа Mathcad 14. Каждое из распределений затем подвергалось идентификации, и каждый результат фиксировался. Итоговые результаты приведены в таблице 2.
По полученным данным в таблице 2 видно, что лучший результат в процессе идентификации таких законов распределения, как экспоненциальный и нормальный, дает «Настройка распределения». Однако данное программное средство имеет наиболее низкие результаты при оценке распределения Рэлея и непрерывного равномерного распределения.
Программное средство «Обработка массивов данных» имеет наилучший результат при идентификации распределения Рэлея, но наихудший для экспоненциального и нормального закона распределения. Программное средство «Knowlaw» наиболее точно идентифицирует равномерное непрерывное распределение, при этом все остальные рассматриваемые законы распределения идентифицируются с не самыми худшими результатами.
Далее проведем проверку на наличие ошибок второго рода. Для этого сгенерируем массивы данных в том же количестве, что и в предыдущей проверке, и имеющих схожие законы распределения, такие как: для проверки идентификации равномерного закона распределения: нормальное и бета-распределение; для проверки идентификации нормального закона распределения: равномерное, гипергеометрическое, биномиальное, логистическое и гамма-распределение; для проверки идентификации экспоненциального закона распределения: распределения Коши, Пуассона, геометрическое и логнормальное распределения; для проверки идентификации закона распределения Рэлея: распределение Вейбулла и гамма-распределение. В результате проведенной проверки получаем величины ошибок второго рода (табл. 3).
По полученным данным в таблице 3 лучший результат для экспоненциального и нормального законов распределения вероятностей имеет программное средство «Настройка распределения».
Таблица 3
Величина ошибки второго рода в процессе идентификации законов распределения программными средствами, %
|
Сравниваемые распределения |
«Настройка распределения» |
«Обработка массивов данных» |
«Knowlaw» |
|
Нормальное |
4,0 |
4,5 |
4,5 |
|
Равномерное непрерывное |
4,0 |
4,0 |
3,0 |
|
Экспоненциальное |
4,5 |
5,5 |
4,5 |
|
Рэлея |
5,0 |
3,0 |
5,5 |
|
Среднее количество ошибок |
4,4 |
4,3 |
4,4 |
Программное средство имеет худший среди рассматриваемых продуктов результат при идентификации равномерного непрерывного распределения.
Программное средство «Обработка массивов данных» наилучший результат показывает при идентификации распределения Рэлея, при этом худший – для нормального и экспоненциального распределений. Программа «Knowlaw» имеет наилучший результат в процессе идентификации равномерного закона распределения. Таким образом, оптимальным методом является программный продукт «Knowlaw». Данный вывод сделан с учетом всех представленных преимуществ, а также меньшей суммарной ошибки первого и второго рода.
Заключение
Результаты исследования эффективности программы для идентификации закона распределения вероятностей «Knowlaw» позволяют сделать вывод, что данная программа – средство с широким функционалом и имеет преимущества перед аналогами. К ним относятся большее число законов распределения, которые удается оценить, а также возможность выбора определенного закона из нескольких вариантов. Кроме того, оценка точности подбора законов показала, что программное средство «Knowlaw» наиболее точно идентифицирует равномерное непрерывное распределение, при этом все остальные рассматриваемые законы распределения идентифицируются с не самыми худшими результатами.



