Проведение предметных олимпиад школьников обусловлено целью выявления и развития творческих способностей и пропаганды научных знаний [1]. В октябре и ноябре проходят школьный и муниципальный этапы Всероссийской олимпиады школьников, школьный этап по шести предметам уже третий год организован на платформе siriusolymp.ru. Это позволяет увеличить количество участников, от школ требуется раздать коды индивидуального доступа и информировать учеников о проходящей олимпиаде и правилах участия. Региональные сайты поддержки олимпиад школьников также способствуют пропаганде знаний и массовости олимпиадного движения. Подготовка школьников к олимпиадам является одним из видов работы с одаренными детьми.
В работе [2] А.И. Савенков описывает ступени познания «любопытство – любознательность – познавательная потребность» и отмечает, что на первой неизбежно оказываются все здоровые дети. Важно, чтобы любопытство переросло в любовь к знаниям (любознательность), а потом и в познавательную потребность. Среди качеств, свойственных одаренному ребенку, одно из ведущих мест занимает сверхчувствительность к проблемам. Развитие этого качества связано с характером обучения (проблемное, ориентированное на самостоятельную исследовательскую работу ребенка). С этой особенностью связана и «познавательная самостоятельность», способность к углублению в проблему. Многие исследователи отмечают склонность одаренных детей к соревновательности, конкуренции. Предметные олимпиады являются одним из способов организации соревнований одаренных детей. В ходе таких соревнований формируется представление о своих возможностях, поддерживается стремление проявить свои способности.
В концепции [3] выделено, что одаренность является системным, развивающимся в течение жизни качеством психики. Работа с одаренными детьми ведется в различных образовательных структурах:
1. В условиях общеобразовательной школы обучение может осуществляться на основе принципов дифференциации и индивидуализации. Отметим, что этот принцип сложно реализовать при традиционном обучении, одним из способов индивидуализации может служить использование электронных образовательных ресурсов, где каждый обучающийся работает в своем темпе, не ждет, когда класс освоит представляемый учителем материал. Дифференциация может быть достигнута назначением более сложных заданий, в том числе с автоматической проверкой на ЭОР.
2. Обучение детей в системе дополнительного образования дает каждому ребенку возможность свободного выбора образовательной области, времени освоения программ, включения в разнообразные виды деятельности с учетом индивидуальных склонностей.
3. Школы, ориентированные на работу с одаренными детьми. В этом случае преимуществом являются однородные группы и возможность достижения наиболее адекватной скорости продвижения в обучении. Однако такое обучение сужает круг общения детей, создает подобие социальных барьеров, формирует у учащихся элитарное сознание.
Л.Г. Петерсон и Н.Х. Агаханов отмечают в методических рекомендациях [4], что организация самостоятельной деятельности позволяет учащимся экспериментировать со своими возможностями. При отборе учебного содержания рекомендуют использовать дифференцированный подход и расширять содержание курса алгебры рассмотрением вопросов математической логики, теории делимости, теории линейных уравнений и неравенств. В каждой теме можно давать отдельным обучающимся задачи «на смекалку», а значит, знакомить школьников с миром «олимпиадных задач». Так появляется возможность подготовить к успешному выступлению на олимпиадах, при наличии желания ученика, или побудить его к размышлению, поиску, развитию, заинтересовать математикой. Целям заинтересовать учеников и разнообразить работу могут служить такие ресурсы, как mob-edu.ru, Учи.ру, ЯКласс.
Материалы и методы исследования
В исследовании использовался сравнительно-сопоставительный анализ методических рекомендаций по организации занятий по подготовке к математическим олимпиадам. А также анализ и обобщение педагогического опыта в процессе работы со школьниками 5–10 классов средней общеобразовательной школы. Исследованы возможности использования для подготовки школьников к олимпиадам платформы mob-edu.ru.
Результаты исследования и их обсуждение
Понимание тонкостей методики и психологии необходимо для успешной подготовки школьников к участию в математических олимпиадах. У обучающихся 5–6 классов широта интересов достигает наибольшей величины, а значит, требуется найти причины решать задачи по математике вместо других занятий.
В работе [5] выделены две основные группы таких причин:
1. Познавательный инстинкт, любознательность, любопытство.
2. Конкуренция, спортивный интерес, потребность в самоутверждении. Кто первым решит задачу? Кто сумеет найти самый легкий метод решения? В коллективе занятие по любому предмету дает возможность для самоутверждения.
Вряд ли возможно научить школьников решать нестандартные, олимпиадные задачи. Но заинтересованного ученика можно развить в этом направлении, если использовать хорошо подобранную методику так, что он захочет и сможет заниматься саморазвитием. В 5–6 классах предпочтительнее решать задачи «россыпью», на разные темы, с повторением и развитием тем, идей и методов от занятия к занятию. А начиная с 7 класса более глубоко разрабатывать на занятии одну тему. Для создания соревновательного момента хорошо вести рейтинг учащихся в течение учебного года. Например, учитывать количество задач, решенных учеником при разных формах контроля и на занятии.
В современных условиях электронные образовательные ресурсы все больше встраиваются в образовательный процесс. Возрастает роль электронных образовательных ресурсов в условиях дистанционного обучения, для реализации принципов дифференциации и индивидуализации обучения. Вопросы использования электронных образовательных ресурсов при изучении математики довольно часто становятся предметом исследований. Онлайн-сервисы и калькуляторы нашли широкое применение в изучении математических дисциплин как во время аудиторных занятий, так и в самостоятельной работе школьников и студентов. Так, особенности применения графического калькулятора Desmos для создания интерактивного задания на построение графика функции описаны в [6]. В работе [7] рассмотрено использование среды GeoGebra и графического калькулятора Desmos в проектной деятельности по математике и моделировании, при осуществлении контроля решения задачи об отделении корней многочлена. Применение ЭОР при подготовке учащихся к олимпиадам по информатике нашло отражение в работе [8], однако именно вопросу использования ЭОР при подготовке к олимпиадам по математике на сегодняшний день не уделялось внимания.
Платформа mob-edu.ru «Мобильное электронное образование» позволяет учителю использовать учебные курсы по предметам в урочной и внеурочной деятельности, а также организовать подготовку к школьным предметным олимпиадам. В библиотеке курсов помимо общеобразовательных предметов, представлены сборники заданий по подготовке к олимпиадам, в том числе и по математике. Олимпиадные задания по математике представлены сборником для 9–11 классов [9].
Каждое задание сборника уникально. Для решения нужно догадаться о пути рассуждений, но при этом нет необходимости в специальных знаниях за рамками школьной программы. Отличительная черта заданий сборника состоит в использовании методов серьезных математических исследований [10]. Это может дать толчок к углубленному изучению теории чисел, комбинаторики, дискретной математики, которые в дальнейшем могут стать инструментом исследований в различных разделах математики [11].
Подготовка школьников к олимпиадам разного уровня выполняет ряд функций [12]:
− образовательная (развитие ведущих общенаучных идей и понятий);
− развивающая (системное мышление, гибкость и самостоятельность ума, познавательная активность);
− воспитывающая (формирование политехнических знаний и умений);
− организационная (выработка единых педагогических требований, сотрудничество педагогов при подготовке олимпиадной предметной команды школьников).
Организация образовательного процесса с использованием цифрового образовательного контента инструментов и сервисов цифровой образовательной среды (ЦОС) в школе способна удовлетворить познавательные интересы, способствует развитию способностей и склонностей каждого школьника [12]. Цифровая образовательная среда дает возможность конструировать собственные продукты, используя уже имеющиеся. В ЦОС МЭО возможен обмен опытом, поиск информации. Встроенные коммуникационные сервисы позволяют выстроить взаимодействие учителя и ученика за счет комментариев, диалогов, обмена текстовыми и мультимедийными файлами. Интернет-уроки как компоненты занятий курсов по математике для каждого класса содержат разнообразные задания с автоматической проверкой в виде теста и в форме заданий с открытым ответом, требующих проверки учителем.
Содержание сборника олимпиадных задач по математике сгруппировано по тематическим модулям. Модули содержат задания разных уровней сложности, соответствующих муниципальному или региональному этапу. В интерактивном содержании можно увидеть название задания, название модуля и уровень сложности от 1 до 10. В сборнике имеется 100 задач, рекомендованных авторами для 9–11 классов, их тематика и количество по каждой теме представлены в таблице.
Тематика сборника олимпиадных задач по математике
|
№ |
Тема |
Номера заданий |
Количество заданий |
|
1 |
Действительные числа |
1–15 |
15 |
|
2 |
Преобразование выражений |
16–30 |
15 |
|
3 |
Уравнения и неравенства |
31–60 |
30 |
|
4 |
Функции. Анализ выражений |
61–71 |
11 |
|
5 |
Функции. Графики |
72–85 |
14 |
|
6 |
Текстовые задачи |
86–100 |
15 |
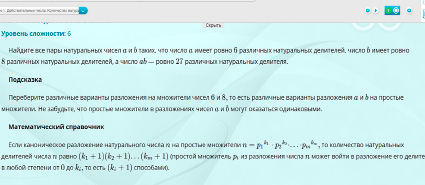
Рис. 1. Формулировка задачи, подсказка и справочная информация

Рис. 2. Ответ и разбор задачи
Отметим, что со многими темами, представленными в сборнике, обучающиеся знакомы с 5–6 класса, а значит, можно решать задачи из сборника при подготовке к олимпиадам гораздо раньше указанных 9–11 классов. Таковы, например, темы делимости натуральных чисел, комбинаторные задачи, текстовые задачи, требующие только арифметических действий и «смекалки». С другой стороны, есть задачи, решение которых невозможно без изучения материала 10–11 классов: логарифм, аркфункции. Таким образом, учителю следует внимательно изучить содержание, прежде чем приступить к использованию сборника.
У сборника удобная структура представления материала курса. В заданиях указаны вспомогательные теоретические сведения, справочная информация и необходимые в конкретном задании формулы. В заданиях высокой сложности учащимся предлагается подсказка, направляющая на путь решения (рис. 1).
Внутри курса и его занятий удобно использовать кнопки навигации в правом верхнем углу для перехода по страницам занятия. На итоговой странице занятия дается полное решение с пояснениями и ответ (рис. 2). Решение и ответ по решению учителя могут быть и открытыми для ученика, и сначала закрытыми.
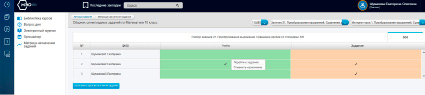
Рис. 3. Матрица назначения заданий
Матрица назначений заданий (рис. 3) – это специализированный инструмент ЦОС МЭО, который позволяет индивидуально каждому ученику назначить задания урока. В матрице назначения заданий представлены все олимпиадные задания Сборника, представляющие собой задания с открытым ответом. Каждому ученику возможно назначить или отменить любое задание. Есть возможность просмотреть задание при назначении без переключения к сборнику, прямо из матрицы. Кнопка слева позволяет установить сроки выполнения заданий. После отправления ответа учеником в матрице учитель видит, что задание выполнено, может выставить отметку, которая появляется в матрице назначений у учителя и у ученика, а также в электронном дневнике.
В случае если ввод ответа или решения с клавиатуры затруднен, можно ответ нарисовать в открывающемся графическом поле, записать аудиоответ или прикрепить файл с ответом в допустимых форматах.
При работе со сборником олимпиадных задач можем назначать как задачу, так и ее разбор, например в случае, если ученик с задачей не справился. Есть возможность для учителя написать комментарий к полученному решению ученика, вложить файл (например, с пояснениями, похожими заданиями или, наоборот, более сложными заданиями по теме).
Материалы учебных курсов ЦОС МЭО удобно использовать при решении задач олимпиад разных уровней и вне сборника, что позволяет учитывать индивидуальные особенности учащихся, конструировать систему заданий, актуальных на сегодняшний день. Например, для 10 класса приводится такая задача: «Про натуральные числа a и b известно, что 4(a + b) = HOД(a, b) + HOK(a, b). Какое наименьшее значение может принимать произведение ab?» В учебном курсе 10 класса темы НОД и НОК нет, эти понятия изучены давно, знания, возможно, потребуется актуализировать. В случае затруднений с решением можно рекомендовать ученику пройти занятие курса математики 6 класса по теме НОД и НОК и назначить задания уроков темы для контроля и потом вернуться к исходной задаче.
Заключение
Олимпиадные задания, представленные в сборнике ЦОС МЭО, не стандартны, следовательно, обеспечивают формирование у учащихся критического мышления и креативности, развивают «гибкость» ума и оригинальность разработки идей. Кроме того, решение олимпиадных заданий Сборника тренирует нестандартность мышления, возможность применять полученные и усвоенные знания в самых разных сферах, развивает уверенность в себе, повышает стрессоустойчивость.
ЦОС МЭО может использоваться как при фронтальной работе в условиях классно-урочной системы, так и с группами учащихся (кружок, факультатив, спецкурс) в рамках внеклассной работы и формате дополнительного образования. Предусмотрена организация индивидуальной самостоятельной работы ученика в сопровождении учителя-предметника.
Работа выполнена при финансовой поддержке ФГБОУ ВО ШГПУ по договору на выполнение научно-исследовательских работ № 16-387 от 15.06.2022 г.



