Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Зачастую испытание сложных технических систем на определенных этапах жизненного цикла значительно эффективнее проводить с помощью имитационной модели. Такой подход позволяет снизить стоимость и время испытаний, обеспечивает более полное тестовое покрытие. При этом необходимым условием успешного завершения испытаний является адекватность модели.

Под имитационной моделью авторы понимают программное обеспечение, которое воспроизводит поведение некоторой реальной системы. Имитационная модель позволяет в комфортных для испытателя условиях многократно повторять эксперименты с различными значениями параметров и получать подробную статистику функционирования системы [1]. Отличительной чертой имитационного моделирования также является возможность управления скоростью течения процессов: время имитации может замедляться в случае с быстропротекающими явлениями или ускоряться для моделирования систем с медленными процессами. Как известно, модель имеет следующие свойства и характеристики [2]:

1) адекватность. Модель должна обеспечивать соответствие объекту в части исследуемых свойств;

2) полнота. Модель должна предоставлять всю необходимую информацию об исследуемом объекте;

3) гибкость. Модель должна предоставлять возможность воспроизведения различных ситуаций в широком диапазоне изменения условий и параметров;

4) чувствительность. Модель должна реагировать на изменения входных данных и корректировать значения выходных данных в соответствии с этими изменениями;

5) точность. Выходные значения модели должны отличаться от выходных значений исследуемого объекта не более чем на заданную величину;

6) устойчивость. Модель должна оставаться адекватной при любых допустимых значениях входных данных и всех возможных параметрах самой модели;

7) масштабируемость. Модель должна поддерживать увеличение объема входных данных, внешних воздействий и выходных значений с сохранением адекватности;

8) производительность. Модель должна выполнять не меньше определенного объема операций за заданный промежуток времени.

Очевидно, что в общем случае одновременное достижение наилучших показателей для всех характеристик невозможно. Например, увеличение точности модели снижает ее производительность. При этом перед разработчиками модели возникает необходимость определения оптимального набора параметров модели, обеспечивающих удовлетворение модели конкретным предъявленным требованиям – ее адекватность решаемой задаче. В свою очередь, такого рода параметрическая перестройка модели накладывает требования на средства имитационного моделирования. Как аппаратная, так и программная их составляющая должны иметь возможность обеспечения характеристик модели во всем динамическом диапазоне.

Схема разработки имитационной модели и ее основные этапы представлены на рис. 1.

Этап 1 – Постановка задачи. Определение структуры исследуемой системы, входных и выходных параметров объекта моделирования, диапазонов их изменения, совокупности ограничений и допущений, требований к характеристикам модели.

Этап 2 – Разработка алгоритмического и математического обеспечения. Описание объектов, среды взаимодействия и процессов средствами математических и алгоритмических моделей и методов. Определение оптимальных методов решения задачи. Предварительная оценка диапазона значений характеристик модели. Методы имитационного моделирования подробно изложены в литературе [3–5].

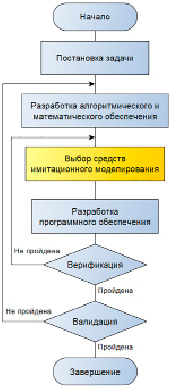
Рис. 1. Схема разработки имитационной модели

Этап 3 – Выбор средств моделирования. Производится выбор программно-аппаратных средств реализации моделей и методов. При выборе средств моделирования учитывается:

− полнота математического аппарата,

− точность вычислений,

− производительность вычислений,

− масштабируемость реализации,

− простота и легкость освоения,

− доступность и стоимость.

Этап 4 – Разработка программного обеспечения. Реализация (кодирование) математического и алгоритмического обеспечения с использованием выбранных программно-аппаратных средств моделирования.

Этап 5 – Верификация. Оценка соответствия результата разработки программного обеспечения. Неудовлетворительные результаты верификации могут стать основанием для изменения средств моделирования.

Этап 6 – Валидация. Оценка соответствия результата разработки математического и алгоритмического обеспечения. Оценка адекватности полученной модели.

Выбор средств имитационного моделирования должен учитывать особенности имитационной модели и является важным этапом при разработке модели. Как аппаратные, так и программные средства должны иметь возможность обеспечения характеристик модели во всем динамическом диапазоне. Неправильный выбор средств имитационного моделирования является одной из причин неудовлетворительных результатов верификации и валидации модели.

Данная статья посвящена исследованию средств имитационного моделирования многомерных сигналов в системах искусственного интеллекта реального времени.

Анализ аппаратных средств имитационного моделирования

Для реализации имитационных моделей многомерных сигналов наряду с вычислительными средствами общего назначения целесообразно применять специализированные вычислительные средства (процессор цифровой обработки сигналов, программируемая логическая интегральная схема), а также устройства формирования и преобразования электрических сигналов.

Вычислительные средства общего назначения находят применение в задачах общего управления и диспетчеризации имитационной модели, а также реализации интерфейса взаимодействия с пользователем.

Процессор цифровой обработки сигналов (ПЦОС) представляет собой специализированный микропроцессор, предназначенный для решения задач цифровой обработки сигналов (далее – ЦОС) [6]. Система команд арифметико-логического устройства ПЦОС оптимизирована для выполнения базовых команд ЦОС, что позволяет существенно увеличить быстродействие по сравнению с вычислителем общего назначения даже при более низкой тактовой частоте ПЦОС.

Программируемая логическая интегральная схема (далее – ПЛИС) представляет собой логическое устройство, логика работы которого задается пользователем посредством программирования [7]. Поскольку ПЛИС последних поколений оснащаются устройствами быстрого умножения, то это позволяет выполнять операцию «умножения с накоплением» с минимальными аппаратными затратами. Наличие микропроцессора в кристалле ПЛИС создает дополнительные возможности в области ЦОС.

В настоящее время существует ряд стандартных многофункциональных модульных платформ (далее – ММП), представляющих собой некоторый стандарт построения аппаратного обеспечения, а также большой набор серийно выпускаемых модулей, соответствующих стандарту. Используя ММП, пользователь может подобрать необходимый набор модулей, содержащих как вычислительные средства общего назначения, так и специализированные вычислители, а также необходимые для решения конкретной задачи формирователи и преобразователи электрических сигналов для сопряжения с реальными объектами. В зависимости от характеристик ММП и инструментов для отладки такое средство может использоваться одновременно для исследований, прототипирования и реализации систем имитационного моделирования. Такой инструмент позволяет снизить трудоемкость моделирования и повысить степень адекватности получаемых результатов за счет использования готовых аппаратных реализаций, позволяющих моделировать сложные процессы.

Разработка собственной ММП требует большого количества времени, ресурсов и квалифицированных специалистов, поэтому имеет смысл использование существующих ММП с отлаженной архитектурой. Недостатком таких средств является их относительно высокая стоимость.

Анализ программных средств имитационного моделирования

Реализация имитационных моделей должна учитывать следующие особенности разработки программного обеспечения:

1) алгоритмы моделирования многомерных сигналов являются параллельными, то есть предполагающими выполнение более чем одного преобразования в каждый момент времени;

2) объем обрабатываемых данных не является детерминированным и требует динамического распределения оперативной памяти;

3) большое количество вычислительных операций связано с математическим аппаратом цифровой обработки сигналов (преобразование Фурье, расчет функции взаимной корреляции, цифровая фильтрация и т.д.);

4) поддержка на уровне библиотек методов искусственного интеллекта (нейросети, глубокое обучение, эволюционное моделирование, экспертные системы);

5) детерминированное время выполнения операций для обеспечения режима реального времени.

Таблица 1

Результаты сравнительного анализа программных средств

С учетом указанных особенностей авторами проведены исследования современных программных средств имитационного моделирования: C/C++, MATLAB, Python, Julia, LabVIEW.

В качестве критериев сравнения были сформулированы следующие:

1) скорость выполнения базовых операций ЦОС (расчет автокорреляционной функции (далее – АКФ) многомерного сигнала, выполнение прямого и обратного быстрого преобразования Фурье (далее – БПФ) многомерного сигнала;

2) погрешность выполнения прямого и обратного БПФ, которая отражает точность вычислений и влияет на точность модели;

3) наличие инструментов визуализации результатов, позволяющих преобразовывать сигналы в изображения и строить графики для анализа результирующих и промежуточных данных;

4) наличие готовых библиотек цифровой обработки сигналов и библиотек для работы с искусственным интеллектом, позволяющих сократить время на разработку и реализацию алгоритмов;

5) поддержка выполнения алгоритмов в режиме реального времени;

6) стоимость и сложность развертывания сред программирования.

Для каждого из языков была установлена среда разработки, подключены необходимые библиотеки для ЦОС и визуализации данных, написан код программ с расчетом АКФ и выполнением прямого и обратного БПФ. В качестве исходного сигнала использовался двумерный массив размерностью 1000x1000 точек, заполненный случайными вещественными числами от нуля до единицы.

Написанные программы состоят:

− из чтения исходного двумерного сигнала из файла,

− сохранения времени до выполнения операций ЦОС,

− выполнения операций ЦОС,

− сохранения времени после выполнения операций ЦОС,

− вывода разницы между временными метками.

Приведенный в статье фрагмент исходного кода для С/C++ содержит только измерение времени расчета АКФ без процедур чтения двумерного сигнала из файла и визуализации рассчитанной АКФ.

В конце программы с выполнением БПФ также сравниваются исходный сигнал и двумерный массив, полученный после прямого и обратного БПФ. Для этого вычисляется разность по модулю между каждым из соответствующих элементов, которая суммируется по всему массиву для получения погрешности выполнения БПФ. Погрешность вычислений возникает из-за ограниченной точности представления чисел в ЭВМ. Для достоверности сравнения в каждом из языков использовался формат представления числа с плавающей точкой, занимающий в памяти 8 байт.

Результаты сравнительного анализа рассмотренных программных средств представлены в табл. 1. Фрагменты исходных кодов и визуализация рассчитанной АКФ приведены в табл. 2 и 3.

Сравнение вычислительной производительности рассматриваемых программных средств было проведено при выполнении трех операций ЦОС: расчета автокорреляционной функции (АКФ), выполнения прямого и обратного быстрого преобразования Фурье (БПФ). При сопоставлении исходного сигнала и полученного после прямого и обратного БПФ оценена точность выполнения операций. Результаты сравнения отражены в гистограммах на рис. 2.

По результатам измерений времени выполнения операций ЦОС особенно выделяются языки C и C++. Остальные языки между собой мало отличаются по скорости выполнения БПФ, а АКФ быстрее рассчитывается с помощью Julia и Python.

Погрешность выполнения БПФ для всех языков имеет одинаковый порядок, где наименее точный результат (LabVIEW) отличается от наиболее точного (Julia) в два раза.

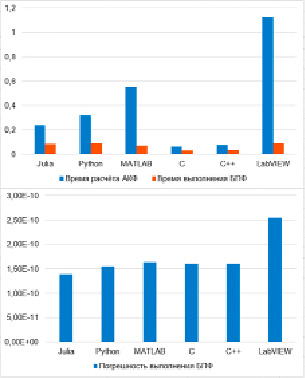
Рис. 2. Сравнение времени выполнения и погрешности алгоритмов АКФ и БПФ

Таблица 2

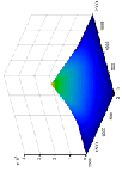
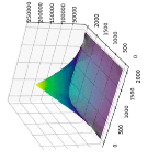
Исходный код вычисления и визуализация АКФ для MATLAB, Python и Julia

Таблица 3

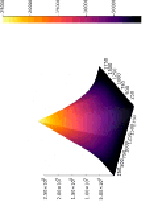
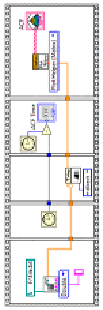
Исходный код вычисления и визуализация АКФ для C/C++ и LabVIEW

Заключение

В данной статье были рассмотрены современные средства имитационного моделирования сигналов.

Для реализации системы имитационного моделирования многомерных сигналов в системах ИИ с поддержкой реального времени предпочтительнее использовать вычислительные устройства специального назначения. Кроме того, прием и формирование физических сигналов требует использования дополнительной аппаратуры, например ММП.

Выбор программного средства реализации имитационной модели нельзя определить однозначно. В том случае, если целью является разработка имитационной модели реального времени с жесткими требованиями по времени выполнения вычислений, из рассматриваемых программных средств наиболее подходящими являются языки программирования C и C++. Программное средство LabVIEW RT может стать эффективным средством прототипирования имитационной модели на базе ММП, так как обеспечивает значительно более «низкий порог входа» разработчика по сравнению с языками C и C++, в том числе обеспечивает поддержку драйверов большой номенклатуры готовых аппаратных модулей и библиотеки программных функций. Такие программные средства, как Python, Julia и MATLAB, с учетом поддержки их библиотеками большого количества необходимых для имитационного моделирования многомерных сигналов функций, но в силу большого времени выполнения операций могут эффективно применяться на стадии прототипирования имитационной модели, разработки алгоритмического и математического обеспечения в тех случаях, когда допустимо пренебрежение ограничениями режима реального времени.

Исследование выполнено за счет гранта Российского научного фонда № 22-11-00049, https://rscf.ru/project/22-11-00049/.