Одним из важных разделов математики является теория многочленов. Особую роль в этом разделе играют симметрические многочлены [1]. Методы, основанные на их применении, позволяют решать следующие задачи: избавление от иррациональности в знаменателе дроби, решение иррациональных уравнений, доказательство тождеств, разложение многочленов на множители, решение систем нелинейных уравнений. Стоит также отметить, что с помощью симметрических многочленов можно решать и достаточно сложные задачи, например, олимпиадного уровня [2].
Цель исследования – познакомиться с симметрическими многочленами и изучить некоторые возможности их применения при решении математических задач повышенного уровня сложности.
1. Симметрические многочлены от двух переменных
Элементарная математика знакомит нас с самыми различными типами задач, начиная от простейших и заканчивая очень трудоёмкими [3].
Решение систем высших степеней, которые достаточно часто встречаются в школьном курсе математики, относится ко второму типу. В качестве примера укажем следующие системы:
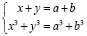 ,
, 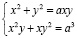 .
.
Общим для этих систем является то, что в обоих случаях и правая, и левая часть уравнений являются многочленами, в которых x и y включены симметричным образом.
Определение. Многочлен от n переменных называется симметрическим, если он переходит в себя при любых перестановках переменных.
Таким образом, многочлен от двух переменных x и y можно считать симметрическим, если он не изменяется при заменах x на y и y на x.
Как известно, любые числа x и y можно переставлять местами при сложении, и сумма этих двух чисел не поменяется, то есть x + y = y + x. Данный многочлен x + y является симметрическим. Подобным же образом многочлен xy – симметрический, если рассматривать закон коммутативности для умножения xy = yx. Рассмотренные симметрические многочлены x + y и xy называют элементарными симметрическими многочленами от x и y. Можно их обозначить следующим образом:
σ1 = x + y, σ2 = xy.
Кроме этих многочленов, важно знать о наличии степенных сумм, таких как 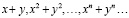 Многочлен
Многочлен 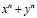 обычно обозначают через sn. То есть
обычно обозначают через sn. То есть
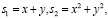
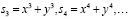
Существует приём, с помощью которого легко можно найти симметрические многочлены. Взяв произвольный многочлен от σ1 и σ2 и подставив в него выражения через x и y, получим симметрический многочлен от x и y (так как σ1 = x + y и σ2 = xy остаются прежними, если поменять местами x и y, следовательно, не поменяется и получившийся многочлен, выраженный через x и y и xy). К примеру, из многочлена 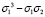 получим симметрический многочлен:
получим симметрический многочлен:
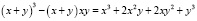 .
.
При любой подстановке симметрических многочленов σ1 = x + y, σ2 = xy в исходное получаем опять же симметрический многочлен от x и y. Является ли данный способ построения симметрических многочленов универсальным и можно ли получить любой симметрический многочлен с помощью него?
Для внесения ясности к данному предположению рассмотрим примеры, выражающие степенные суммы через σ1 и σ2:
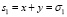 ,
,
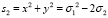 ,
,
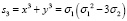 ,
,
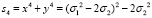 .
.
Разобравшись в данных примерах, можно прийти к выводу: произвольный симметрический многочлен можно выражать через элементарные симметрические многочлены σ1 и σ2, использовав математические преобразования.
Теорема (основная теорема о симметрических многочленах). Любой симметрический многочлен от двух переменных x и y можно представить в виде симметрического многочлена от элементарных симметрических многочленов σ1 = x + y и σ2 = xy.
1.1, Решение систем уравнений с помощью симметрических уравнений от двух переменных
Заменяя неизвестные x и y элементарными симметрическими многочленами σ1 = x + y и σ2 = xy, можно получить более простую систему, так как в исходных уравнениях уменьшаются степени после замены, потому что σ2 = xy – это многочлен второй степени от x и y. Следовательно, решать систему уравнений относительно новых неизвестных σ1 и σ2 становится проще.
Не стоит забывать, что, так как исходная система зависит от неизвестных x и y, то в ответе мы должны записать значения этих величин, то есть выразить σ1 и σ2 через x и y. Данное действие можно сделать, применив теорему.
Теорема. Пусть даны:
σ1 и σ2 – два произвольных числа;
квадратное уравнение 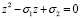 ;
;
система уравнений 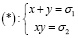 .
.
Они связаны друг с другом следующим образом:
- если z1 и z2 – корни квадратного уравнения, то система (*) имеет только два решения:
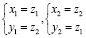 ;
;
- обратно, если x = a, y = b является решением системы (*), то числа a и b являются корнями квадратного уравнения.
Большое количество систем из двух уравнений поддаются более легкому выводу корней, если применить симметрические многочлены при их решении. В этом случае мы вводим вспомогательные неизвестные. При применении этого способа подстановок не всегда удаётся прийти к более легкому виду выражения, чем было прежде, поэтому важно правильно сориентироваться в самом начале.
2. Симметрические многочлены от трёх переменных
Перейдем к рассмотрению многочленов от трех переменных x, y, z: в них можно сделать не одну перестановку, а три – поменять местами x и y, или x и z, или z и y. Иначе говоря, если многочлен остаётся неизменным при любой возможной перестановке его переменных, то его можно назвать симметрическим.
Определение. Многочлен от трёх переменных f (x, y, z) называется симметрическим, если он не изменяется ни при какой перестановке переменных.
Симметричность многочлена задаётся условием
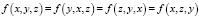 .
.
Данные многочлены строятся подобно симметрическим многочленам от двух переменных, которые рассматривались выше. Элементарные симметрические многочлены от трех переменных имеют вид:
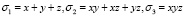 .
.
Нетрудно заметить, что σ1 – многочлен первой степени, σ2 – второй, σ3 – третьей.
Степенные суммы 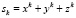 также симметричны, причем каждая из них может быть представлена в виде многочлена от σ1, σ2, σ3.
также симметричны, причем каждая из них может быть представлена в виде многочлена от σ1, σ2, σ3.
Замена в произвольно выбранном многочлене любых трёх переменных σ1, σ2, σ3 на элементарные симметрические многочлены позволяет нам получить самый легкий способ построения симметрических многочленов от трёх переменных. Это даст нам многочлен, симметрично зависящий от x, y, z. К примеру, 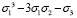 можно представить как
можно представить как
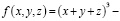
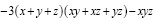 .
.
С помощью некоторых преобразований можно прийти к симметрическому многочлену 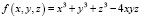 .
.
Справедлива теорема:
Теорема (основная теорема о симметрических многочленах от трех переменных). Любой симметрический многочлен от x, y, z можно представить в виде многочлена от
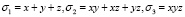 .
.
Симметрические многочлены от x, y, z могут быть полезны при решении ряда задач: решение различных систем уравнений с тремя неизвестными, разложение выражений на множители, доказательство тождеств, решение неравенств, освобождение от иррациональности в знаменателе и т.д. [4, 5].
2.1. Разложение многочлена на множители
Положим, что f(x, y, z) – симметрический многочлен от трёх переменных. Для начала стоит попытаться записать его через σ1, σ2, σ3. Далее получившееся выражение можно уже попробовать раскладывать на множители путем подстановки значений элементарных симметрических многочленов
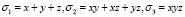 .
.
Иногда перед раскрытием скобок выгоднее упростить заданное выражение, введя только частично симметрические многочлены σ1, σ2, σ3. То есть введение σ1, σ2, σ3 только в некоторых частях исходного выражения, сохранив при этом некое количество первоначальных переменных x, y, z, бывает полезным для более легких вычислений при решении различных задач. Рассмотрим пример:
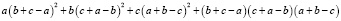 .
.
Заданный многочлен преобразуется следующим образом:
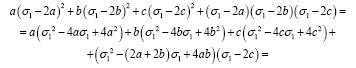
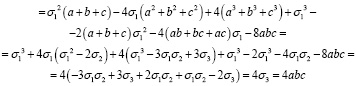
Стоит отметить, что указанные приёмы применимы только тогда, когда есть возможность раскладывать симметрический многочлен на симметрические множители.
2. 2. Освобождение от иррациональности в знаменателе
Одними из сложных задач в математике считаются задачи с иррациональными выражениями в знаменателях. В случаях, когда знаменателями являются выражения 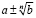 или
или 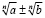 , задачу еще можно более или менее легко решить, применив лишь то, что мы знаем из основной базы математических операций. Но встречаются и более сложные задачи, когда в знаменателе содержатся три или более иррациональных слагаемых. В этом случае и применимы симметрические многочлены.
, задачу еще можно более или менее легко решить, применив лишь то, что мы знаем из основной базы математических операций. Но встречаются и более сложные задачи, когда в знаменателе содержатся три или более иррациональных слагаемых. В этом случае и применимы симметрические многочлены.
Рассмотрим дробь
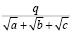 ,
,
в которой нужно иррациональность знаменателя заменить неким более простым выражением. Положим 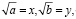
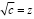 . В этом случае выражение в знаменателе примет вид самого простого элементарного симметрического многочлена σ1 = x + y + z. Далее нужно найти такой множитель, умножение на который приведет к возможности выражения знаменателя через степенные суммы s2, s4.
. В этом случае выражение в знаменателе примет вид самого простого элементарного симметрического многочлена σ1 = x + y + z. Далее нужно найти такой множитель, умножение на который приведет к возможности выражения знаменателя через степенные суммы s2, s4.
Они имеют вид:
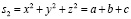 ,
,
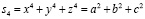 .
.
После всего этого знаменатель уже будет не иррациональным. При нахождении этого множителя потребуются формулы:
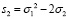 ,
,
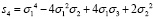 .
.
Если рассмотреть эти степенные суммы внимательно, то несложно увидеть, что в обоих случаях все слагаемые, кроме последнего (справа), являются кратными σ1. Чтобы было удобнее работать с данными выражениями, можно сделать некоторое комбинирование степенных сумм, вследствие чего получится избавиться от тех последних некратных слагаемых, которые только «мешали». Это возможно, если взять квадрат от s2 и вычесть из него удвоенную s4. Получится:
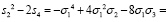
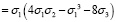 ,
,
Откуда
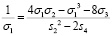 (*)
(*)
В исходных данных были: 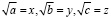 , поэтому находим
, поэтому находим
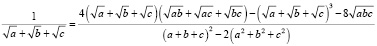
Замечание. Употребление степенной суммы 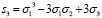 для правой части формулы даёт возможность удобнее и проще выразить
для правой части формулы даёт возможность удобнее и проще выразить 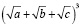 , без громоздкости при преобразовании скобок. То есть исходную формулу (*) имеем право переписать как
, без громоздкости при преобразовании скобок. То есть исходную формулу (*) имеем право переписать как
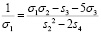 .
.
На основании этого (полагая 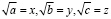 ), можно прийти к решению более удобным способом:
), можно прийти к решению более удобным способом:
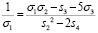 .
.
Откуда
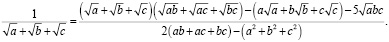
Задача решена – знаменатель стал рациональным. Применим её для рассмотрения следующего примера, уже более общего вида. Пусть вопрос поставлен такой же, как и в предыдущем примере: сделать рациональным знаменатель у дроби
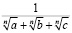 ,
,
то есть задача состоит в следующем преобразовании:
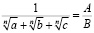 ,
,
где A – это выражение, которое может быть сколь угодно сложного вида, а B – может быть только рациональным. Очевидно, что такой знаменатель получается лишь тогда, когда включены n-е степени корней 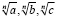 . Если введём обозначения
. Если введём обозначения 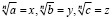 , то останется найти тождество:
, то останется найти тождество:
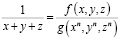 ,
,
где g и f – некоторые многочлены. Преобразуем запись как
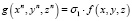 .
.
Значит, задача состоит в отыскании многочлена 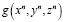 , кратного элементарному симметрическому многочлену σ1 = x + y + z. Как же это можно сделать? Если взять зависящие только от n-х степеней переменных x, y, z симметрические многочлены, то придём к степенным суммам, а точнее, к
, кратного элементарному симметрическому многочлену σ1 = x + y + z. Как же это можно сделать? Если взять зависящие только от n-х степеней переменных x, y, z симметрические многочлены, то придём к степенным суммам, а точнее, к
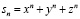 ,
,
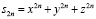 ,
,
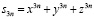 и т.д.
и т.д.
Вспомним из предыдущего примера, что к решению можно прийти в том случае, если многочлен g будет делиться на σ1, а этого можно добиться при комбинации и преобразовании данных степенных сумм.
Данное действие комбинирования sn, s2n, s3n, … является не такой легкой задачей, но с помощью этого мы придём к тому, что многочлен g будет кратен σ1. Тут обычно немного «жульничают» и используют не только степенные суммы, а еще и σ1 = xyz. То есть наряду с рациональными выражениями sn, s2n, s3n, … используем одновременно и иррациональное 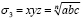 . Так как при
. Так как при 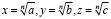 имеем
имеем 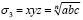 , т.е. в ряд рациональных выражений sn, s2n, s3n, … добавляется только одна иррациональность
, т.е. в ряд рациональных выражений sn, s2n, s3n, … добавляется только одна иррациональность 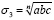 . А освобождение от данного корня, рассмотренное в начале, не вызывает трудностей.
. А освобождение от данного корня, рассмотренное в начале, не вызывает трудностей.
Стоит отметить и недостаток описанного метода: выражение sn, s2n, s3n, … через σ1, σ2, σ3 при увеличении показателей корней становится тяжелее из-за усложнения подбора нужных комбинаций этих степенных сумм. А также описанный метод применим только тогда, когда знаменатель включает в себя не более трёх корней.
Подобные задачи на освобождение от иррациональности могут формулироваться и немного по-иному, в общем виде: избавиться от иррациональности соотношения
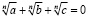 .
.
То есть нужно найти рациональное соотношение между a, b и c, которое выполняется в случае, когда равенство 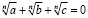 имеет место быть. Легко понять, что есть тесная связь с этой задачей и с рассмотренными выше. Пусть
имеет место быть. Легко понять, что есть тесная связь с этой задачей и с рассмотренными выше. Пусть 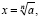
 . Тогда справедливо будет написать
. Тогда справедливо будет написать
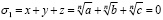 .
.
В случае, когда комбинация степенных сумм приведёт к нахождению многочлена g, такого что
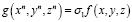 ,
,
то подстановкой σ1 = 0 можно увидеть, что 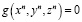 . Таким образом, мы нашли требуемое рациональное соотношение (так как
. Таким образом, мы нашли требуемое рациональное соотношение (так как 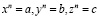 ). При решении таких типов задач существенно упрощает работу таблица степенных сумм sn, s2n, s3n, … которая может использоваться как шпаргалка.
). При решении таких типов задач существенно упрощает работу таблица степенных сумм sn, s2n, s3n, … которая может использоваться как шпаргалка.
Заключение
Теория симметрических многочленов выходит за рамки школьного курса математики, однако знания по этой теме могут быть полезны при решении целого ряда указанных выше задач. Они позволяют решать следующие задачи: освобождение знаменателя дроби от иррациональности, извлечение корней, разложение выражений на множители более простого вида, понижение степени уравнения, решение систем нелинейных уравнений. Кроме того, симметрические многочлены тесно связаны с изучением формул Виета. Также стоит отметить, что с помощью таких многочленов можно найти решение задач ЕГЭ, олимпиадных задач, заданий централизованных проверочных работ. Таким образом, изучение симметрических многочленов и их приложений актуально не только для тех, кто занимается углубленно математикой, а также для тех, кто ищет альтернативные и легкие пути решения школьных задач.
Работа выполнена за счет средств Программы стратегического академического лидерства Казанского (Приволжского) федерального университета.



